Multi-Agent Online Control with Adversarial Disturbances

Multi-agent control problems involving a large number of agents with competing and time-varying objectives are increasingly prevalent in applications across robotics, economics, and energy systems. In this paper, we study online control in multi-agent linear dynamical systems with disturbances. In contrast to most prior work in multi-agent control, we consider an online setting where disturbances are adversarial and where each agent seeks to minimize its own, adversarial sequence of convex losses. In this setting, we investigate the robustness of gradient-based controllers from single-agent online control, with a particular focus on understanding how individual regret guarantees are influenced by the number of agents in the system. Under minimal communication assumptions, we prove near-optimal sublinear regret bounds that hold uniformly for all agents. Finally, when the objectives of the agents are aligned, we show that the multi-agent control problem induces a time-varying potential game for which we derive equilibrium gap guarantees.

Fast and Furious Symmetric Learning in Zero-Sum Games: Gradient Descent as Fictitious Play

This paper investigates the sublinear regret guarantees of two non-no-regret algorithms in zero-sum games: Fictitious Play, and Online Gradient Descent with constant stepsizes. In general adversarial online learning settings, both algorithms may exhibit instability and linear regret due to no regularization (Fictitious Play) or small amounts of regularization (Gradient Descent). However, their ability to obtain tighter regret bounds in two-player zero-sum games is less understood. In this work, we obtain strong new regret guarantees for both algorithms on a class of symmetric zero-sum games that generalize the classic three-strategy Rock-Paper-Scissors to a weighted, n-dimensional regime. Under symmetric initializations of the players' strategies, we prove that Fictitious Play with any tiebreaking rule has $O(\sqrt{T})$ regret, establishing a new class of games for which Karlin's Fictitious Play conjecture holds. Moreover, by leveraging a connection between the geometry of the iterates of Fictitious Play and Gradient Descent in the dual space of payoff vectors, we prove that Gradient Descent, for almost all symmetric initializations, obtains a similar $O(\sqrt{T})$ regret bound when its stepsize is a sufficiently large constant. For Gradient Descent, this establishes the first "fast and furious" behavior (i.e., sublinear regret without time-vanishing stepsizes) for zero-sum games larger than 2x2.

Optimistic Online Learning in Symmetric Cone Games

Optimistic online learning algorithms have led to significant advances in equilibrium computation, particularly for two-player zero-sum games, achieving an iteration complexity of $\mathcal{O}(1/\epsilon)$ to reach an $\epsilon$-saddle point. These advances have been established in normal-form games, where strategies are simplex vectors, and quantum games, where strategies are trace-one positive semidefinite matrices. We extend optimistic learning to symmetric cone games (SCGs), a class of two-player zero-sum games where strategy spaces are generalized simplices (trace-one slices of symmetric cones). A symmetric cone is the cone of squares of a Euclidean Jordan Algebra; canonical examples include the nonnegative orthant, the second-order cone, the cone of positive semidefinite matrices, and their products, all fundamental to convex optimization. SCGs unify normal-form and quantum games and, as we show, offer significantly greater modeling flexibility, allowing us to model applications such as distance metric learning problems and the Fermat-Weber problem. To compute approximate saddle points in SCGs, we introduce the Optimistic Symmetric Cone Multiplicative Weights Update algorithm and establish an iteration complexity of $\mathcal{O}(1/\epsilon)$ to reach an $\epsilon$-saddle point. Our analysis builds on the Optimistic Follow-the-Regularized-Leader framework, with a key technical contribution being a new proof of the strong convexity of the symmetric cone negative entropy with respect to the trace-one norm, a result that may be of independent interest.

Decentralized Learning Dynamics in the Gossip Model

We study a distributed multi-armed bandit setting among a population of $n$ memory-constrained nodes in the gossip model: at each round, every node locally adopts one of $m$ arms, observes a reward drawn from the arm's (adversarially chosen) distribution, and then communicates with a randomly sampled neighbor, exchanging information to determine its policy in the next round. We introduce and analyze several families of dynamics for this task that are decentralized: each node's decision is entirely local and depends only on its most recently obtained reward and that of the neighbor it sampled. We show a connection between the global evolution of these decentralized dynamics with a certain class of "zero-sum" multiplicative weight update algorithms, and we develop a general framework for analyzing the population-level regret of these natural protocols. Using this framework, we derive sublinear regret bounds under a wide range of parameter regimes (i.e., the size of the population and number of arms) for both the stationary reward setting (where the mean of each arm's distribution is fixed over time) and the adversarial reward setting (where means can vary over time). Further, we show that these protocols can approximately optimize convex functions over the simplex when the reward distributions are generated from a stochastic gradient oracle.

Differentially Private Maximal Information Coefficients

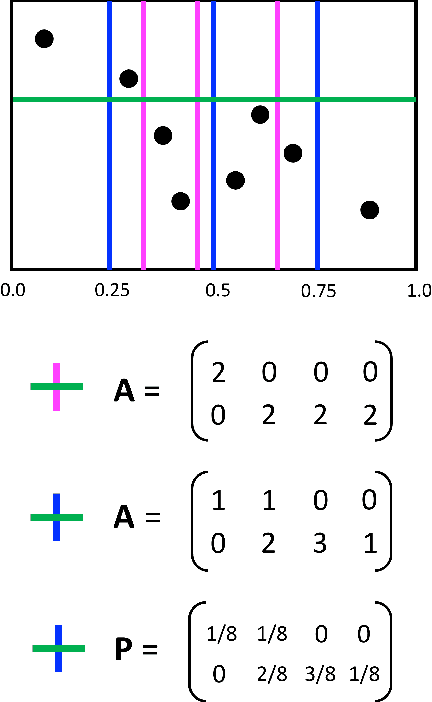
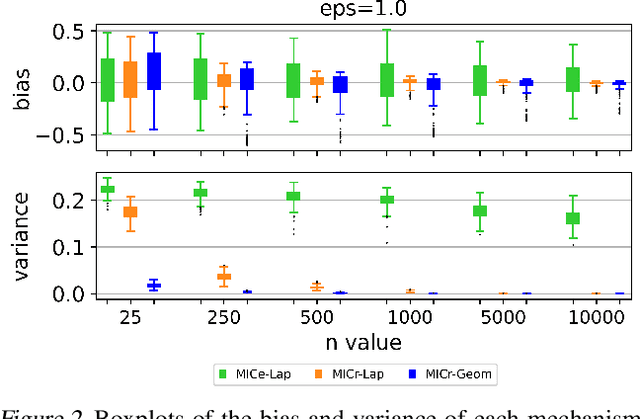
The Maximal Information Coefficient (MIC) is a powerful statistic to identify dependencies between variables. However, it may be applied to sensitive data, and publishing it could leak private information. As a solution, we present algorithms to approximate MIC in a way that provides differential privacy. We show that the natural application of the classic Laplace mechanism yields insufficient accuracy. We therefore introduce the MICr statistic, which is a new MIC approximation that is more compatible with differential privacy. We prove MICr is a consistent estimator for MIC, and we provide two differentially private versions of it. We perform experiments on a variety of real and synthetic datasets. The results show that the private MICr statistics significantly outperform direct application of the Laplace mechanism. Moreover, experiments on real-world datasets show accuracy that is usable when the sample size is at least moderately large.

Consistency of the Maximal Information Coefficient Estimator

The Maximal Information Coefficient (MIC) of Reshef et al. (Science, 2011) is a statistic for measuring dependence between variable pairs in large datasets. In this note, we prove that MIC is a consistent estimator of the corresponding population statistic MIC$_*$. This corrects an error in an argument of Reshef et al. (JMLR, 2016), which we describe.