Differentially Private Maximal Information Coefficients

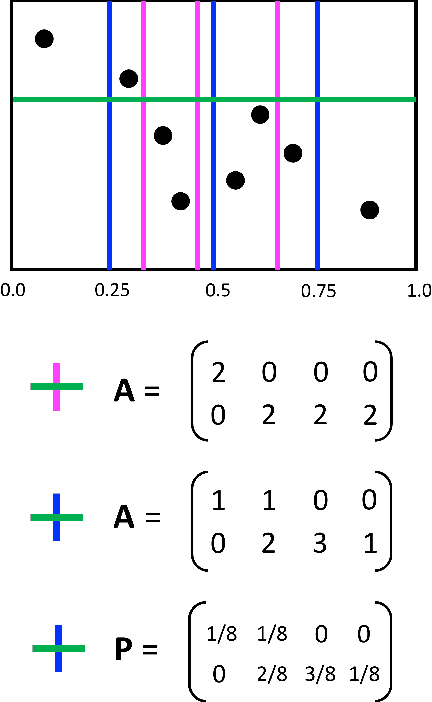
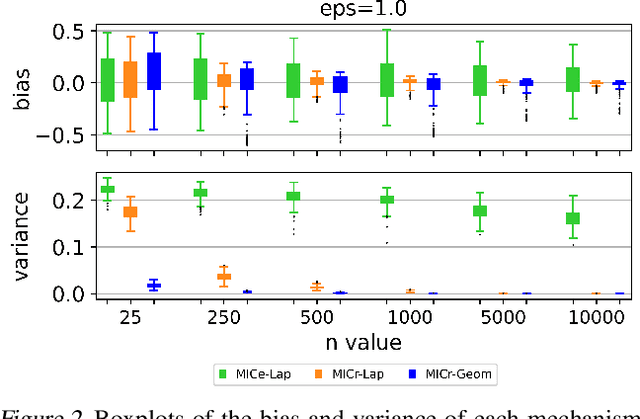
The Maximal Information Coefficient (MIC) is a powerful statistic to identify dependencies between variables. However, it may be applied to sensitive data, and publishing it could leak private information. As a solution, we present algorithms to approximate MIC in a way that provides differential privacy. We show that the natural application of the classic Laplace mechanism yields insufficient accuracy. We therefore introduce the MICr statistic, which is a new MIC approximation that is more compatible with differential privacy. We prove MICr is a consistent estimator for MIC, and we provide two differentially private versions of it. We perform experiments on a variety of real and synthetic datasets. The results show that the private MICr statistics significantly outperform direct application of the Laplace mechanism. Moreover, experiments on real-world datasets show accuracy that is usable when the sample size is at least moderately large.

Consistency of the Maximal Information Coefficient Estimator

The Maximal Information Coefficient (MIC) of Reshef et al. (Science, 2011) is a statistic for measuring dependence between variable pairs in large datasets. In this note, we prove that MIC is a consistent estimator of the corresponding population statistic MIC$_*$. This corrects an error in an argument of Reshef et al. (JMLR, 2016), which we describe.