John Lafferty
University of Chicago
Sequential Nonparametric Regression
Jun 27, 2012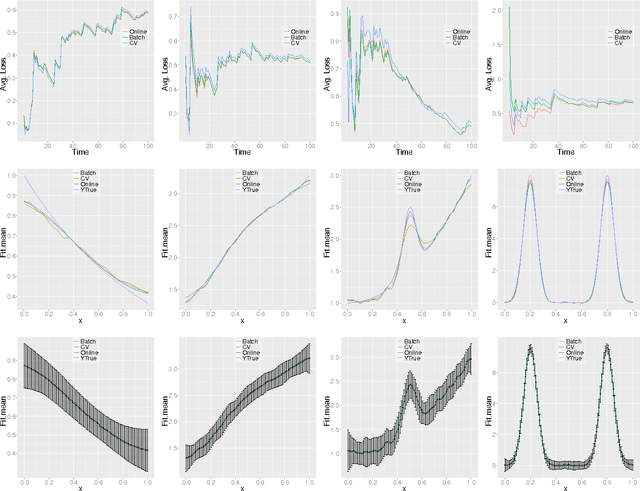

Abstract:We present algorithms for nonparametric regression in settings where the data are obtained sequentially. While traditional estimators select bandwidths that depend upon the sample size, for sequential data the effective sample size is dynamically changing. We propose a linear time algorithm that adjusts the bandwidth for each new data point, and show that the estimator achieves the optimal minimax rate of convergence. We also propose the use of online expert mixing algorithms to adapt to unknown smoothness of the regression function. We provide simulations that confirm the theoretical results, and demonstrate the effectiveness of the methods.
The Nonparanormal SKEPTIC
Jun 27, 2012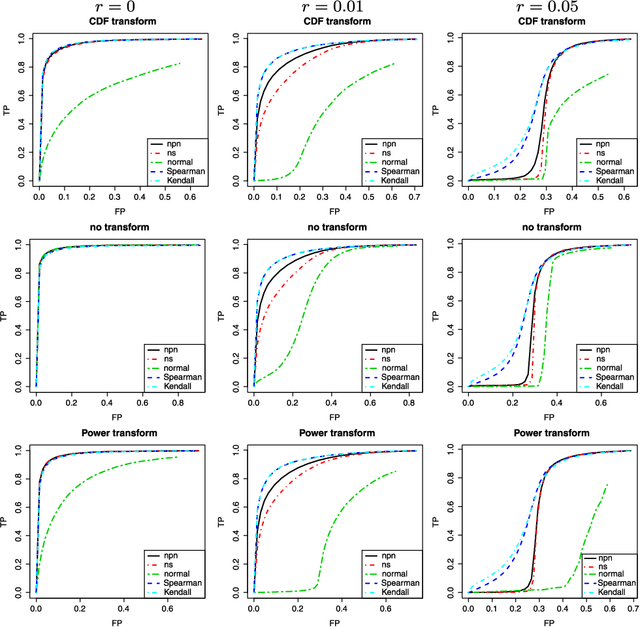
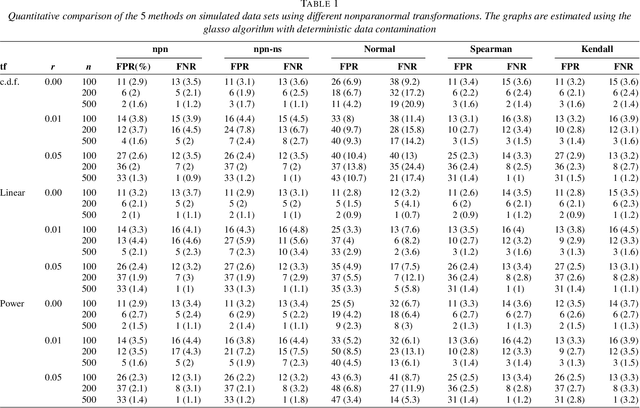
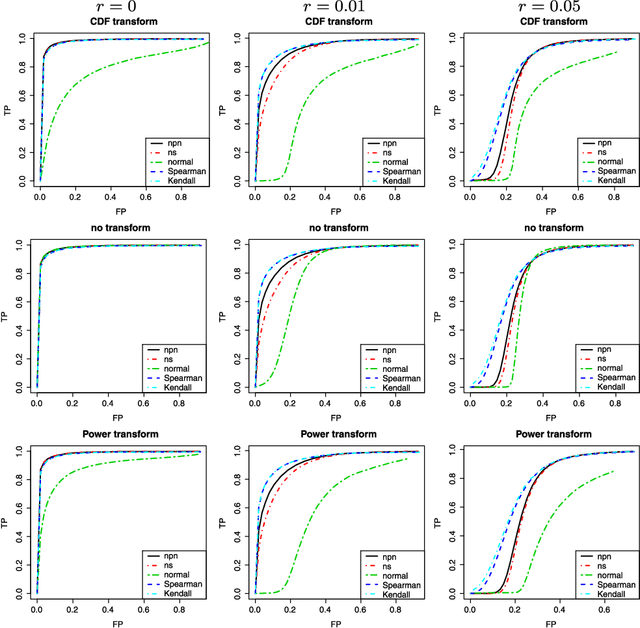
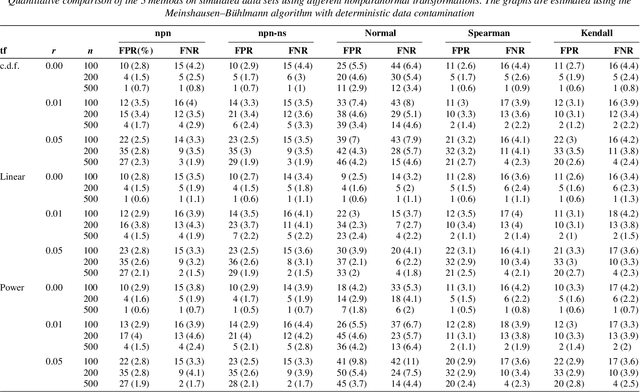
Abstract:We propose a semiparametric approach, named nonparanormal skeptic, for estimating high dimensional undirected graphical models. In terms of modeling, we consider the nonparanormal family proposed by Liu et al (2009). In terms of estimation, we exploit nonparametric rank-based correlation coefficient estimators including the Spearman's rho and Kendall's tau. In high dimensional settings, we prove that the nonparanormal skeptic achieves the optimal parametric rate of convergence in both graph and parameter estimation. This result suggests that the nonparanormal graphical models are a safe replacement of the Gaussian graphical models, even when the data are Gaussian.
Sparse Additive Functional and Kernel CCA
Jun 18, 2012
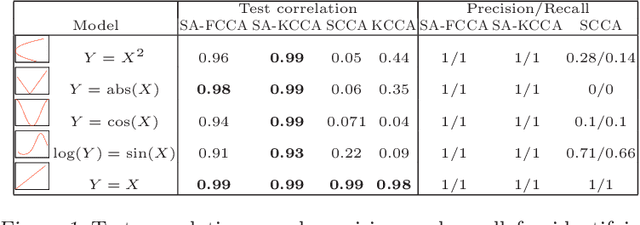
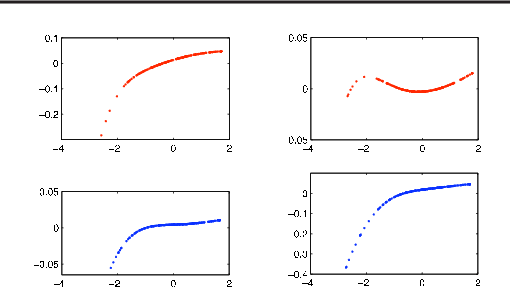
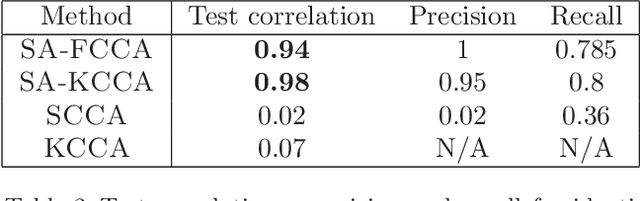
Abstract:Canonical Correlation Analysis (CCA) is a classical tool for finding correlations among the components of two random vectors. In recent years, CCA has been widely applied to the analysis of genomic data, where it is common for researchers to perform multiple assays on a single set of patient samples. Recent work has proposed sparse variants of CCA to address the high dimensionality of such data. However, classical and sparse CCA are based on linear models, and are thus limited in their ability to find general correlations. In this paper, we present two approaches to high-dimensional nonparametric CCA, building on recent developments in high-dimensional nonparametric regression. We present estimation procedures for both approaches, and analyze their theoretical properties in the high-dimensional setting. We demonstrate the effectiveness of these procedures in discovering nonlinear correlations via extensive simulations, as well as through experiments with genomic data.
Forest Density Estimation
Oct 20, 2010


Abstract:We study graph estimation and density estimation in high dimensions, using a family of density estimators based on forest structured undirected graphical models. For density estimation, we do not assume the true distribution corresponds to a forest; rather, we form kernel density estimates of the bivariate and univariate marginals, and apply Kruskal's algorithm to estimate the optimal forest on held out data. We prove an oracle inequality on the excess risk of the resulting estimator relative to the risk of the best forest. For graph estimation, we consider the problem of estimating forests with restricted tree sizes. We prove that finding a maximum weight spanning forest with restricted tree size is NP-hard, and develop an approximation algorithm for this problem. Viewing the tree size as a complexity parameter, we then select a forest using data splitting, and prove bounds on excess risk and structure selection consistency of the procedure. Experiments with simulated data and microarray data indicate that the methods are a practical alternative to Gaussian graphical models.
Union Support Recovery in Multi-task Learning
Aug 31, 2010
Abstract:We sharply characterize the performance of different penalization schemes for the problem of selecting the relevant variables in the multi-task setting. Previous work focuses on the regression problem where conditions on the design matrix complicate the analysis. A clearer and simpler picture emerges by studying the Normal means model. This model, often used in the field of statistics, is a simplified model that provides a laboratory for studying complex procedures.
Graph-Valued Regression
Jun 21, 2010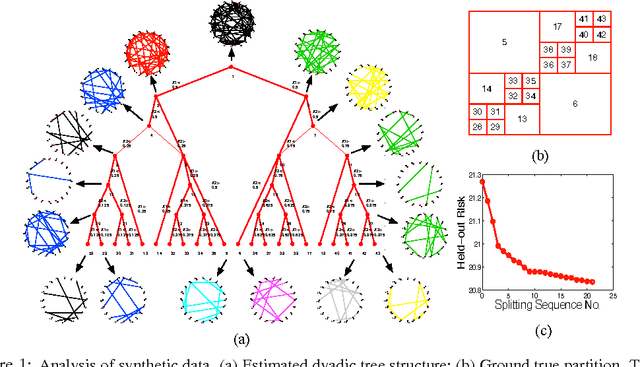

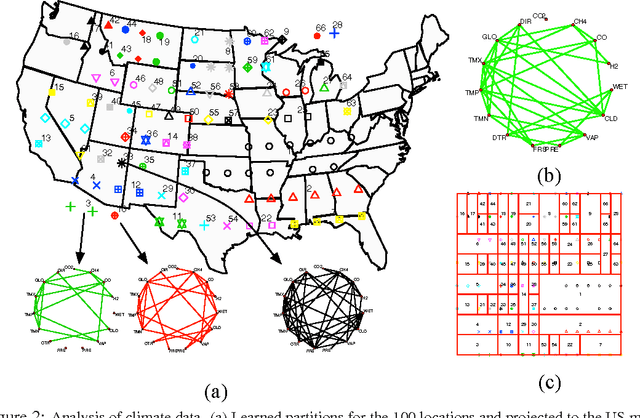
Abstract:Undirected graphical models encode in a graph $G$ the dependency structure of a random vector $Y$. In many applications, it is of interest to model $Y$ given another random vector $X$ as input. We refer to the problem of estimating the graph $G(x)$ of $Y$ conditioned on $X=x$ as ``graph-valued regression.'' In this paper, we propose a semiparametric method for estimating $G(x)$ that builds a tree on the $X$ space just as in CART (classification and regression trees), but at each leaf of the tree estimates a graph. We call the method ``Graph-optimized CART,'' or Go-CART. We study the theoretical properties of Go-CART using dyadic partitioning trees, establishing oracle inequalities on risk minimization and tree partition consistency. We also demonstrate the application of Go-CART to a meteorological dataset, showing how graph-valued regression can provide a useful tool for analyzing complex data.
The Nonparanormal: Semiparametric Estimation of High Dimensional Undirected Graphs
Mar 03, 2009
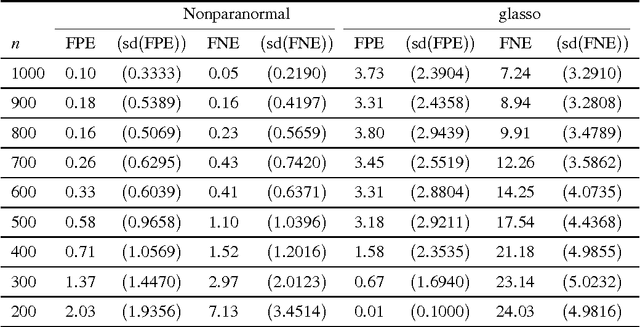
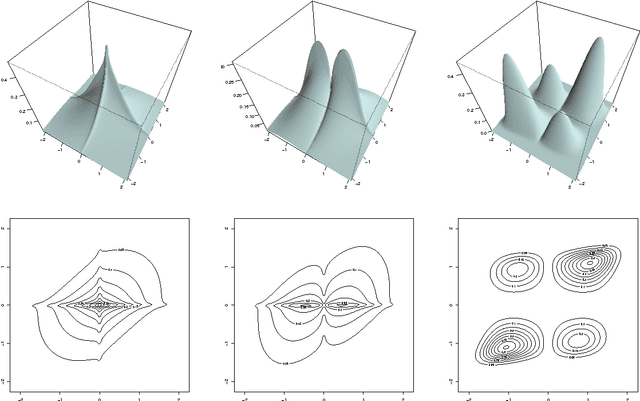
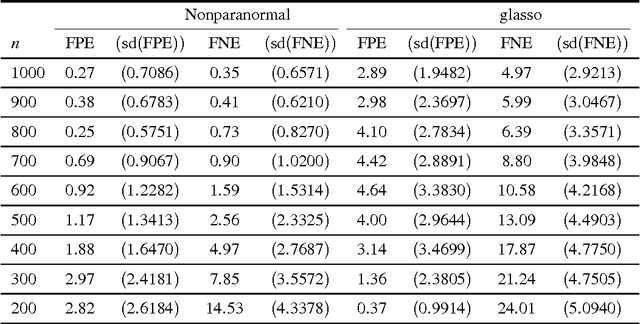
Abstract:Recent methods for estimating sparse undirected graphs for real-valued data in high dimensional problems rely heavily on the assumption of normality. We show how to use a semiparametric Gaussian copula--or "nonparanormal"--for high dimensional inference. Just as additive models extend linear models by replacing linear functions with a set of one-dimensional smooth functions, the nonparanormal extends the normal by transforming the variables by smooth functions. We derive a method for estimating the nonparanormal, study the method's theoretical properties, and show that it works well in many examples.
Time Varying Undirected Graphs
Apr 29, 2008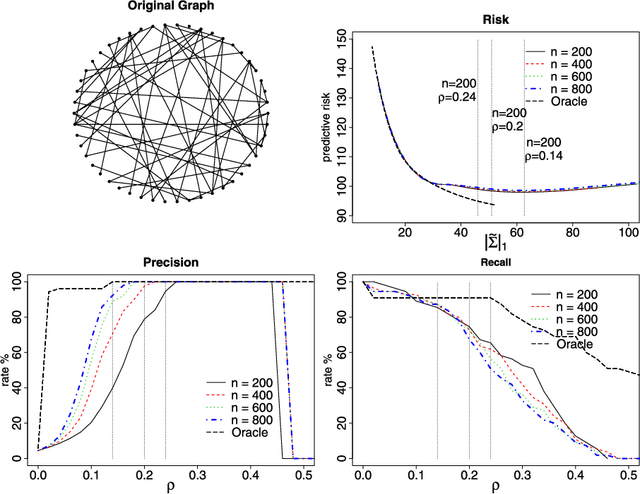
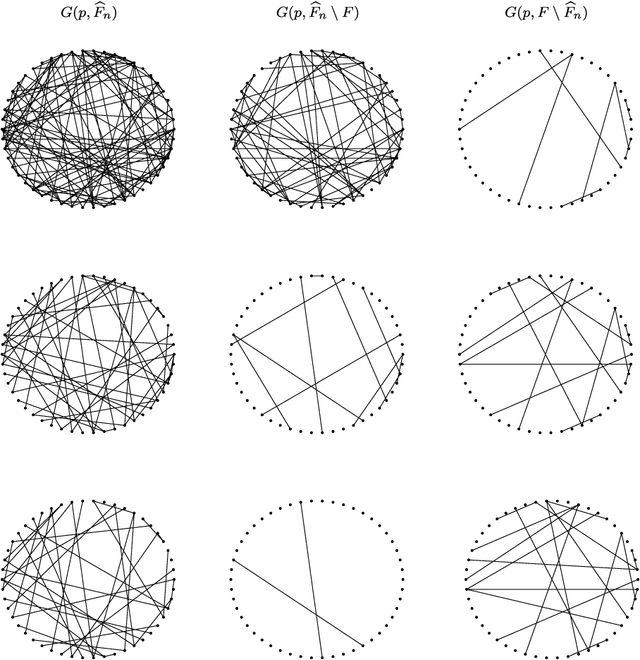
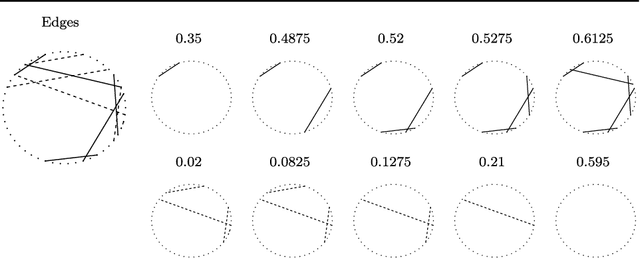
Abstract:Undirected graphs are often used to describe high dimensional distributions. Under sparsity conditions, the graph can be estimated using $\ell_1$ penalization methods. However, current methods assume that the data are independent and identically distributed. If the distribution, and hence the graph, evolves over time then the data are not longer identically distributed. In this paper, we show how to estimate the sequence of graphs for non-identically distributed data, where the distribution evolves over time.
* 12 pages, 3 figures, to appear in COLT 2008
Compressed Regression
Jan 11, 2008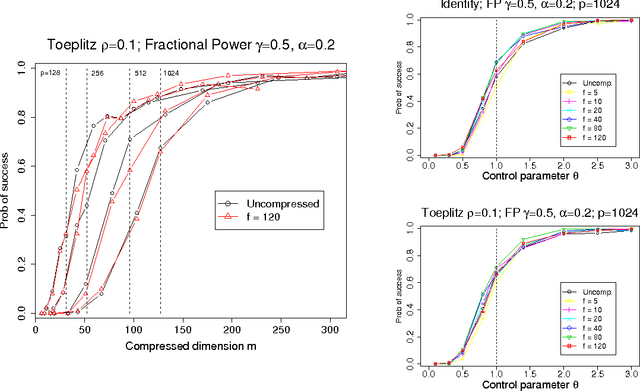
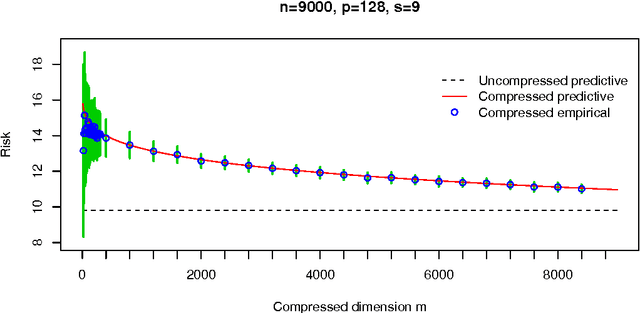
Abstract:Recent research has studied the role of sparsity in high dimensional regression and signal reconstruction, establishing theoretical limits for recovering sparse models from sparse data. This line of work shows that $\ell_1$-regularized least squares regression can accurately estimate a sparse linear model from $n$ noisy examples in $p$ dimensions, even if $p$ is much larger than $n$. In this paper we study a variant of this problem where the original $n$ input variables are compressed by a random linear transformation to $m \ll n$ examples in $p$ dimensions, and establish conditions under which a sparse linear model can be successfully recovered from the compressed data. A primary motivation for this compression procedure is to anonymize the data and preserve privacy by revealing little information about the original data. We characterize the number of random projections that are required for $\ell_1$-regularized compressed regression to identify the nonzero coefficients in the true model with probability approaching one, a property called ``sparsistence.'' In addition, we show that $\ell_1$-regularized compressed regression asymptotically predicts as well as an oracle linear model, a property called ``persistence.'' Finally, we characterize the privacy properties of the compression procedure in information-theoretic terms, establishing upper bounds on the mutual information between the compressed and uncompressed data that decay to zero.
* 59 pages, 5 figure, Submitted for review
A Model of Lexical Attraction and Repulsion
Jun 16, 1997
Abstract:This paper introduces new methods based on exponential families for modeling the correlations between words in text and speech. While previous work assumed the effects of word co-occurrence statistics to be constant over a window of several hundred words, we show that their influence is nonstationary on a much smaller time scale. Empirical data drawn from English and Japanese text, as well as conversational speech, reveals that the ``attraction'' between words decays exponentially, while stylistic and syntactic contraints create a ``repulsion'' between words that discourages close co-occurrence. We show that these characteristics are well described by simple mixture models based on two-stage exponential distributions which can be trained using the EM algorithm. The resulting distance distributions can then be incorporated as penalizing features in an exponential language model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge