Learning Regularization Functionals for Inverse Problems: A Comparative Study

In recent years, a variety of learned regularization frameworks for solving inverse problems in imaging have emerged. These offer flexible modeling together with mathematical insights. The proposed methods differ in their architectural design and training strategies, making direct comparison challenging due to non-modular implementations. We address this gap by collecting and unifying the available code into a common framework. This unified view allows us to systematically compare the approaches and highlight their strengths and limitations, providing valuable insights into their future potential. We also provide concise descriptions of each method, complemented by practical guidelines.

Training NTK to Generalize with KARE

The performance of the data-dependent neural tangent kernel (NTK; Jacot et al. (2018)) associated with a trained deep neural network (DNN) often matches or exceeds that of the full network. This implies that DNN training via gradient descent implicitly performs kernel learning by optimizing the NTK. In this paper, we propose instead to optimize the NTK explicitly. Rather than minimizing empirical risk, we train the NTK to minimize its generalization error using the recently developed Kernel Alignment Risk Estimator (KARE; Jacot et al. (2020)). Our simulations and real data experiments show that NTKs trained with KARE consistently match or significantly outperform the original DNN and the DNN- induced NTK (the after-kernel). These results suggest that explicitly trained kernels can outperform traditional end-to-end DNN optimization in certain settings, challenging the conventional dominance of DNNs. We argue that explicit training of NTK is a form of over-parametrized feature learning.

Noisier2Inverse: Self-Supervised Learning for Image Reconstruction with Correlated Noise

We propose Noisier2Inverse, a correction-free self-supervised deep learning approach for general inverse prob- lems. The proposed method learns a reconstruction function without the need for ground truth samples and is ap- plicable in cases where measurement noise is statistically correlated. This includes computed tomography, where detector imperfections or photon scattering create correlated noise patterns, as well as microscopy and seismic imaging, where physical interactions during measurement introduce dependencies in the noise structure. Similar to Noisier2Noise, a key step in our approach is the generation of noisier data from which the reconstruction net- work learns. However, unlike Noisier2Noise, the proposed loss function operates in measurement space and is trained to recover an extrapolated image instead of the original noisy one. This eliminates the need for an extrap- olation step during inference, which would otherwise suffer from ill-posedness. We numerically demonstrate that our method clearly outperforms previous self-supervised approaches that account for correlated noise.

Sparse2Inverse: Self-supervised inversion of sparse-view CT data

Sparse-view computed tomography (CT) enables fast and low-dose CT imaging, an essential feature for patient-save medical imaging and rapid non-destructive testing. In sparse-view CT, only a few projection views are acquired, causing standard reconstructions to suffer from severe artifacts and noise. To address these issues, we propose a self-supervised image reconstruction strategy. Specifically, in contrast to the established Noise2Inverse, our proposed training strategy uses a loss function in the projection domain, thereby bypassing the otherwise prescribed nullspace component. We demonstrate the effectiveness of the proposed method in reducing stripe-artifacts and noise, even from highly sparse data.

Single-Image based unsupervised joint segmentation and denoising

In this work, we develop an unsupervised method for the joint segmentation and denoising of a single image. To this end, we combine the advantages of a variational segmentation method with the power of a self-supervised, single-image based deep learning approach. One major strength of our method lies in the fact, that in contrast to data-driven methods, where huge amounts of labeled samples are necessary, our model can segment an image into multiple meaningful regions without any training database. Further, we introduce a novel energy functional in which denoising and segmentation are coupled in a way that both tasks benefit from each other. The limitations of existing single-image based variational segmentation methods, which are not capable of dealing with high noise or generic texture, are tackled by this specific combination with self-supervised image denoising. We propose a unified optimisation strategy and show that, especially for very noisy images available in microscopy, our proposed joint approach outperforms its sequential counterpart as well as alternative methods focused purely on denoising or segmentation. Another comparison is conducted with a supervised deep learning approach designed for the same application, highlighting the good performance of our approach.

Variational multichannel multiclass segmentation\endgraf using unsupervised lifting with CNNs

We propose an unsupervised image segmentation approach, that combines a variational energy functional and deep convolutional neural networks. The variational part is based on a recent multichannel multiphase Chan-Vese model, which is capable to extract useful information from multiple input images simultaneously. We implement a flexible multiclass segmentation method that divides a given image into $K$ different regions. We use convolutional neural networks (CNNs) targeting a pre-decomposition of the image. By subsequently minimising the segmentation functional, the final segmentation is obtained in a fully unsupervised manner. Special emphasis is given to the extraction of informative feature maps serving as a starting point for the segmentation. The initial results indicate that the proposed method is able to decompose and segment the different regions of various types of images, such as texture and medical images and compare its performance with another multiphase segmentation method.

A Joint Variational Multichannel Multiphase Segmentation Framework

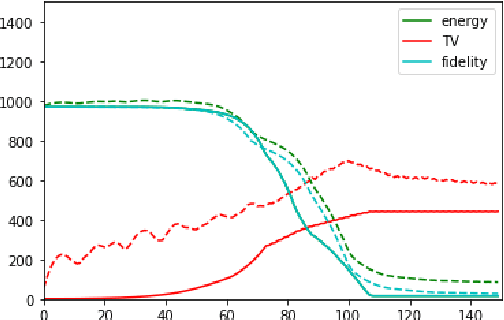
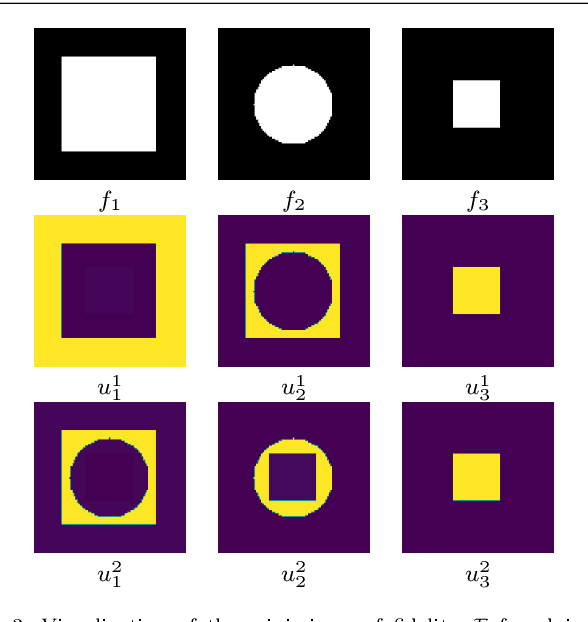
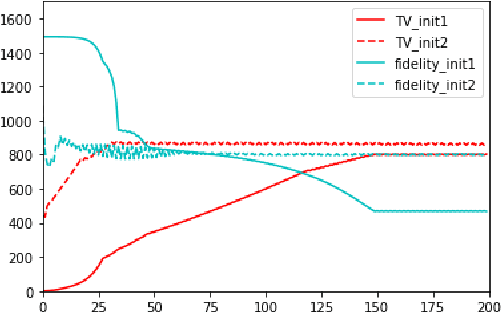
In this paper, we propose a variational image segmentation framework for multichannel multiphase image segmentation based on the Chan-Vese active contour model. The core of our method lies in finding a variable u encoding the segmentation, by minimizing a multichannel energy functional that combines the information of multiple images. We create a decomposition of the input, either by multichannel filtering, or simply by using plain natural RGB, or medical images, which already consist of several channels. Subsequently we minimize the proposed functional for each of the channels simultaneously. Our model meets the necessary assumptions such that it can be solved efficiently by optimization techniques like the Chambolle-Pock method. We prove that the proposed energy functional has global minimizers, and show its stability and convergence with respect to noisy inputs. Experimental results show that the proposed method performs well in single- and multichannel segmentation tasks, and can be employed to the segmentation of various types of images, such as natural and texture images as well as medical images.

Sparse aNETT for Solving Inverse Problems with Deep Learning

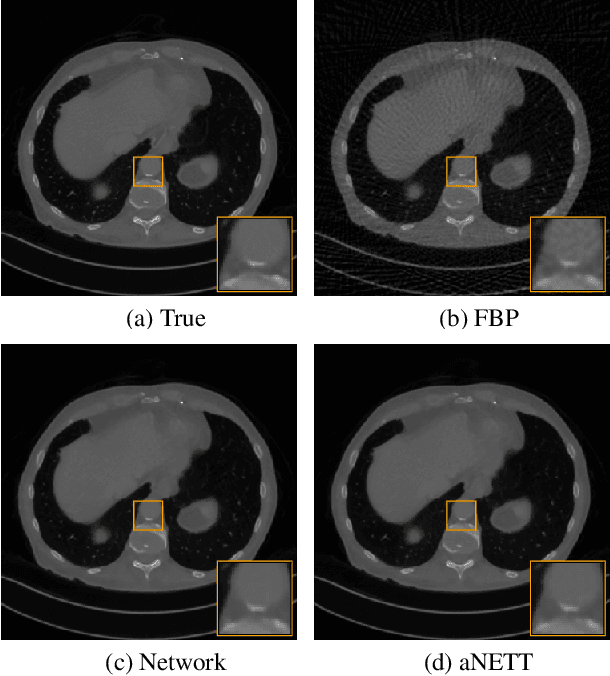
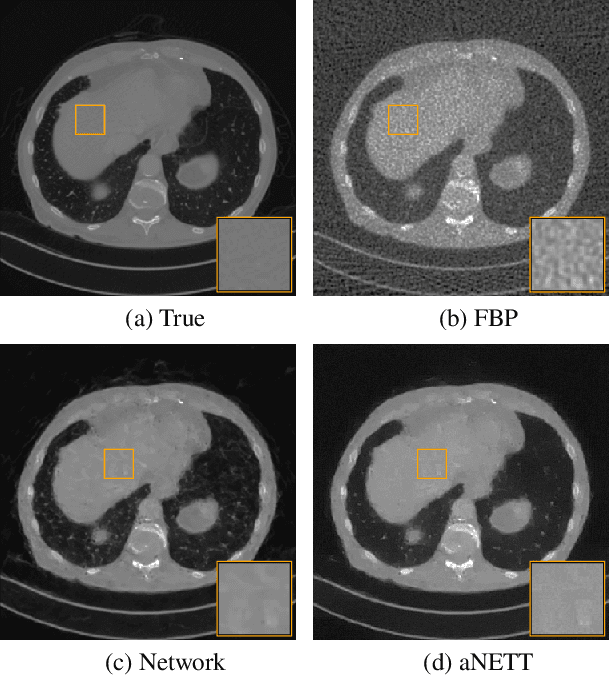
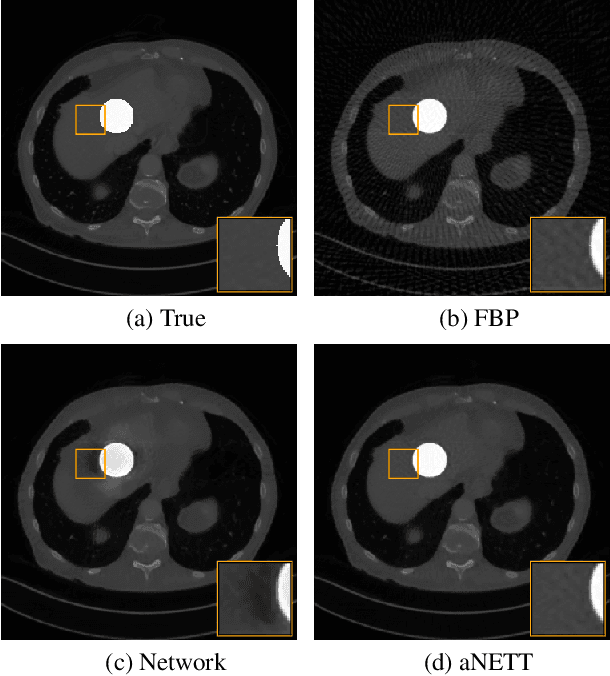
We propose a sparse reconstruction framework (aNETT) for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an autoencoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform and minimize a Tikhonov functional with learned regularizer formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. We propose a strategy for training an autoencoder based on a sample set of the underlying image class such that the autoencoder is independent of the forward operator and is subsequently adapted to the specific forward model. Numerical results are presented for sparse view CT, which clearly demonstrate the feasibility, robustness and the improved generalization capability and stability of aNETT over post-processing networks.

Deep synthesis regularization of inverse problems

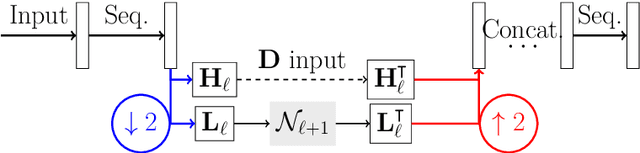
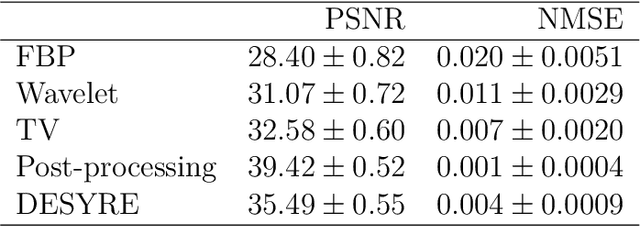
Recently, a large number of efficient deep learning methods for solving inverse problems have been developed and show outstanding numerical performance. For these deep learning methods, however, a solid theoretical foundation in the form of reconstruction guarantees is missing. In contrast, for classical reconstruction methods, such as convex variational and frame-based regularization, theoretical convergence and convergence rate results are well established. In this paper, we introduce deep synthesis regularization (DESYRE) using neural networks as nonlinear synthesis operator bridging the gap between these two worlds. The proposed method allows to exploit the deep learning benefits of being well adjustable to available training data and on the other hand comes with a solid mathematical foundation. We present a complete convergence analysis with convergence rates for the proposed deep synthesis regularization. We present a strategy for constructing a synthesis network as part of an analysis-synthesis sequence together with an appropriate training strategy. Numerical results show the plausibility of our approach.

Sparse $\ell^q$-regularization of inverse problems with deep learning

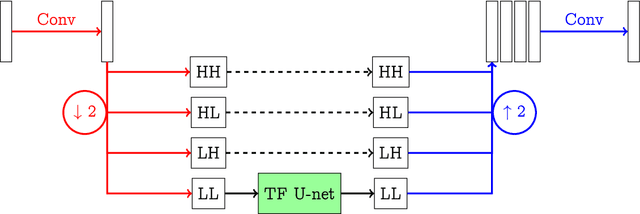
We propose a sparse reconstruction framework for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an encoder-decoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform. We minimize a Tikhonov functional which used a learned regularization term formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. For this augmented sparse $\ell^q$-approach, we present a full convergence analysis, derive convergence rates and describe a training strategy. As a main ingredient for the analysis we establish the coercivity of the augmented regularization term.