Training NTK to Generalize with KARE

The performance of the data-dependent neural tangent kernel (NTK; Jacot et al. (2018)) associated with a trained deep neural network (DNN) often matches or exceeds that of the full network. This implies that DNN training via gradient descent implicitly performs kernel learning by optimizing the NTK. In this paper, we propose instead to optimize the NTK explicitly. Rather than minimizing empirical risk, we train the NTK to minimize its generalization error using the recently developed Kernel Alignment Risk Estimator (KARE; Jacot et al. (2020)). Our simulations and real data experiments show that NTKs trained with KARE consistently match or significantly outperform the original DNN and the DNN- induced NTK (the after-kernel). These results suggest that explicitly trained kernels can outperform traditional end-to-end DNN optimization in certain settings, challenging the conventional dominance of DNNs. We argue that explicit training of NTK is a form of over-parametrized feature learning.

A Simple Algorithm For Scaling Up Kernel Methods

The recent discovery of the equivalence between infinitely wide neural networks (NNs) in the lazy training regime and Neural Tangent Kernels (NTKs) (Jacot et al., 2018) has revived interest in kernel methods. However, conventional wisdom suggests kernel methods are unsuitable for large samples due to their computational complexity and memory requirements. We introduce a novel random feature regression algorithm that allows us (when necessary) to scale to virtually infinite numbers of random features. We illustrate the performance of our method on the CIFAR-10 dataset.

Benign Autoencoders

The success of modern machine learning algorithms depends crucially on efficient data representation and compression through dimensionality reduction. This practice seemingly contradicts the conventional intuition suggesting that data processing always leads to information loss. We prove that this intuition is wrong. For any non-convex problem, there exists an optimal, benign auto-encoder (BAE) extracting a lower-dimensional data representation that is strictly beneficial: Compressing model inputs improves model performance. We prove that BAE projects data onto a manifold whose dimension is the compressibility dimension of the learning model. We develop and implement an efficient algorithm for computing BAE and show that BAE improves model performance in every dataset we consider. Furthermore, by compressing "malignant" data dimensions, BAE makes learning more stable and robust.

Deep Regression Ensembles

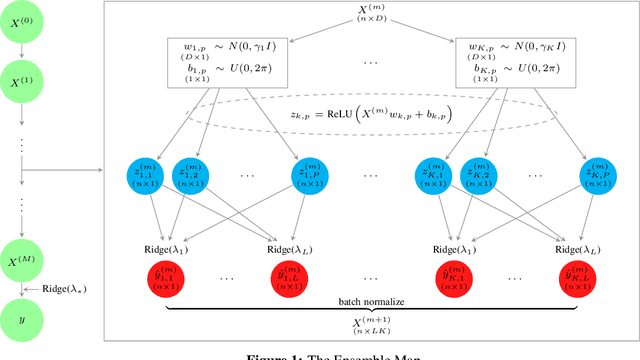
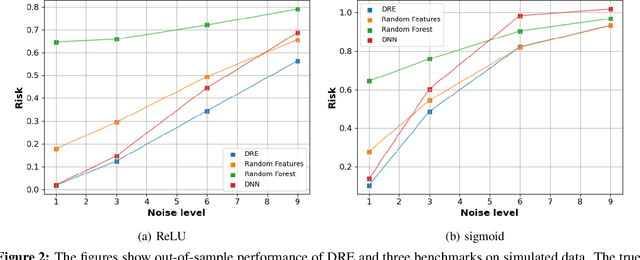
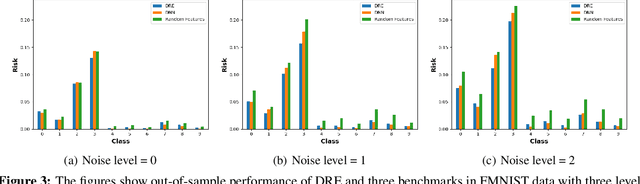
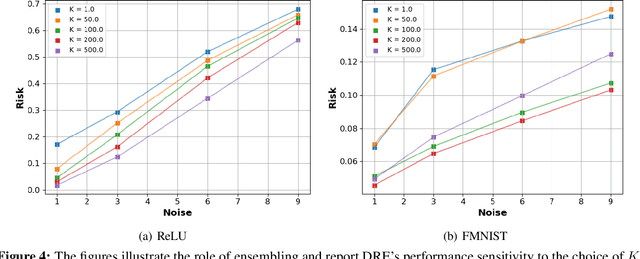
We introduce a methodology for designing and training deep neural networks (DNN) that we call "Deep Regression Ensembles" (DRE). It bridges the gap between DNN and two-layer neural networks trained with random feature regression. Each layer of DRE has two components, randomly drawn input weights and output weights trained myopically (as if the final output layer) using linear ridge regression. Within a layer, each neuron uses a different subset of inputs and a different ridge penalty, constituting an ensemble of random feature ridge regressions. Our experiments show that a single DRE architecture is at par with or exceeds state-of-the-art DNN in many data sets. Yet, because DRE neural weights are either known in closed-form or randomly drawn, its computational cost is orders of magnitude smaller than DNN.

Persuasion by Dimension Reduction

How should an agent (the sender) observing multi-dimensional data (the state vector) persuade another agent to take the desired action? We show that it is always optimal for the sender to perform a (non-linear) dimension reduction by projecting the state vector onto a lower-dimensional object that we call the "optimal information manifold." We characterize geometric properties of this manifold and link them to the sender's preferences. Optimal policy splits information into "good" and "bad" components. When the sender's marginal utility is linear, revealing the full magnitude of good information is always optimal. In contrast, with concave marginal utility, optimal information design conceals the extreme realizations of good information and only reveals its direction (sign). We illustrate these effects by explicitly solving several multi-dimensional Bayesian persuasion problems.