Facets in Argumentation: A Formal Approach to Argument Significance

Argumentation is a central subarea of Artificial Intelligence (AI) for modeling and reasoning about arguments. The semantics of abstract argumentation frameworks (AFs) is given by sets of arguments (extensions) and conditions on the relationship between them, such as stable or admissible. Today's solvers implement tasks such as finding extensions, deciding credulous or skeptical acceptance, counting, or enumerating extensions. While these tasks are well charted, the area between decision, counting/enumeration and fine-grained reasoning requires expensive reasoning so far. We introduce a novel concept (facets) for reasoning between decision and enumeration. Facets are arguments that belong to some extensions (credulous) but not to all extensions (skeptical). They are most natural when a user aims to navigate, filter, or comprehend the significance of specific arguments, according to their needs. We study the complexity and show that tasks involving facets are much easier than counting extensions. Finally, we provide an implementation, and conduct experiments to demonstrate feasibility.

Proceedings of the twelfth Workshop on Answer Set Programming and Other Computing Paradigms 2019

This is the Proceedings of the twelfth Workshop on Answer Set Programming and Other Computing Paradigms (ASPOCP) 2019, which was held in Philadelphia, USA, June 3rd , 2019.

Proceedings of the elevent Workshop on Answer Set Programming and Other Computing Paradigms 2018

This is the Proceedings of the elevent Workshop on Answer Set Programming and Other Computing Paradigms (ASPOCP) 2018, which was held in Oxford, UK, July 18th, 2018.

Answer Set Solving with Bounded Treewidth Revisited

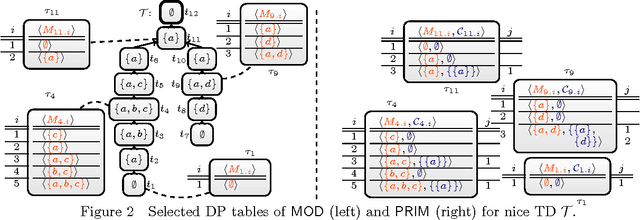
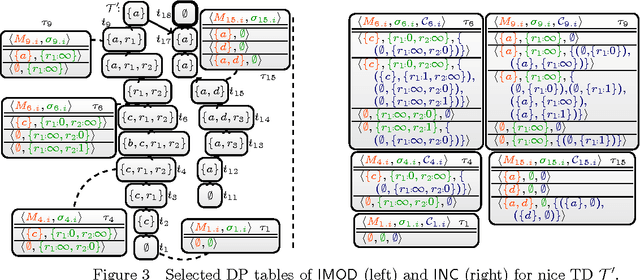
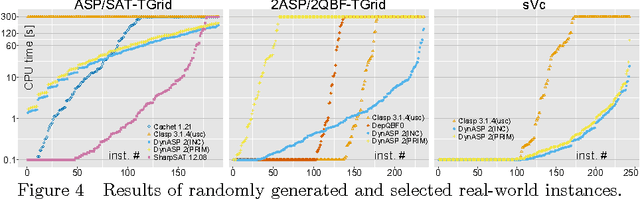
Parameterized algorithms are a way to solve hard problems more efficiently, given that a specific parameter of the input is small. In this paper, we apply this idea to the field of answer set programming (ASP). To this end, we propose two kinds of graph representations of programs to exploit their treewidth as a parameter. Treewidth roughly measures to which extent the internal structure of a program resembles a tree. Our main contribution is the design of parameterized dynamic programming algorithms, which run in linear time if the treewidth and weights of the given program are bounded. Compared to previous work, our algorithms handle the full syntax of ASP. Finally, we report on an empirical evaluation that shows good runtime behaviour for benchmark instances of low treewidth, especially for counting answer sets.

Counting Answer Sets via Dynamic Programming

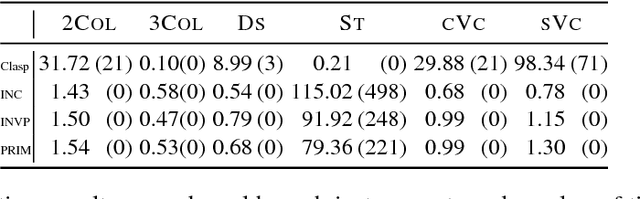
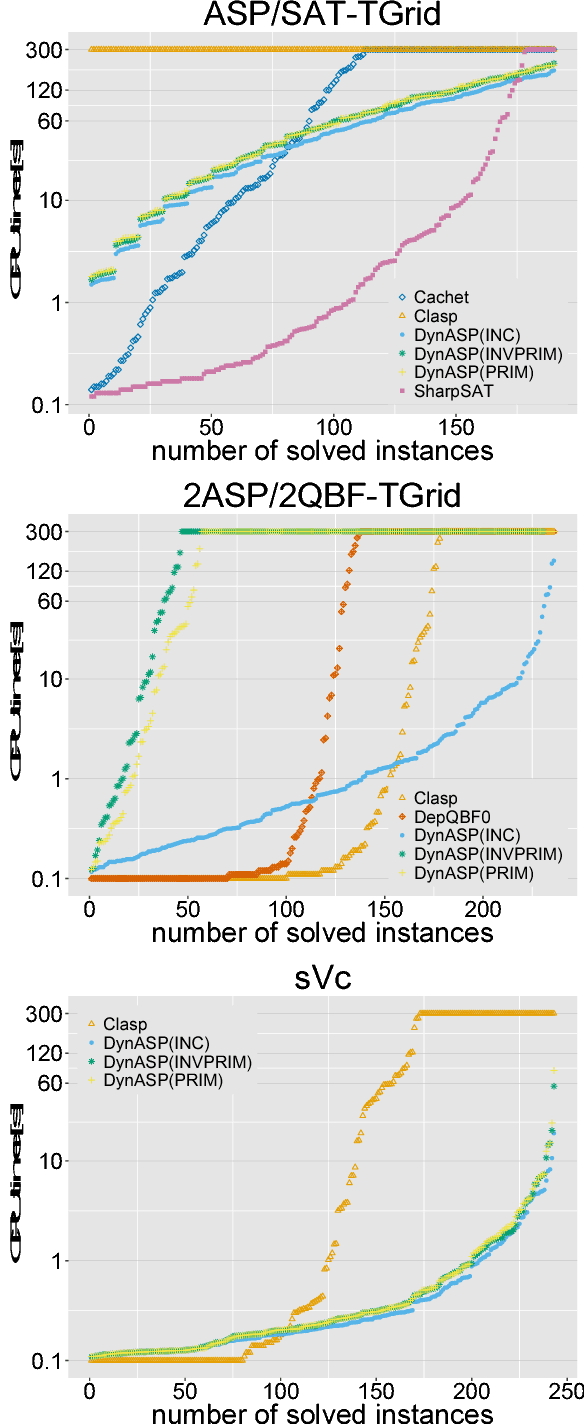
While the solution counting problem for propositional satisfiability (#SAT) has received renewed attention in recent years, this research trend has not affected other AI solving paradigms like answer set programming (ASP). Although ASP solvers are designed to enumerate all solutions, and counting can therefore be easily done, the involved materialization of all solutions is a clear bottleneck for the counting problem of ASP (#ASP). In this paper we propose dynamic programming-based #ASP algorithms that exploit the structure of the underlying (ground) ASP program. Experimental results for a prototype implementation show promise when compared to existing solvers.