Sobolev Training of End-to-End Optimization Proxies

Optimization proxies - machine learning models trained to approximate the solution mapping of parametric optimization problems in a single forward pass - offer dramatic reductions in inference time compared to traditional iterative solvers. This work investigates the integration of solver sensitivities into such end to end proxies via a Sobolev training paradigm and does so in two distinct settings: (i) fully supervised proxies, where exact solver outputs and sensitivities are available, and (ii) self supervised proxies that rely only on the objective and constraint structure of the underlying optimization problem. By augmenting the standard training loss with directional derivative information extracted from the solver, the proxy aligns both its predicted solutions and local derivatives with those of the optimizer. Under Lipschitz continuity assumptions on the true solution mapping, matching first order sensitivities is shown to yield uniform approximation error proportional to the training set covering radius. Empirically, different impacts are observed in each studied setting. On three large Alternating Current Optimal Power Flow benchmarks, supervised Sobolev training cuts mean squared error by up to 56 percent and the median worst case constraint violation by up to 400 percent while keeping the optimality gap below 0.22 percent. For a mean variance portfolio task trained without labeled solutions, self supervised Sobolev training halves the average optimality gap in the medium risk region (standard deviation above 10 percent of budget) and matches the baseline elsewhere. Together, these results highlight Sobolev training whether supervised or self supervised as a path to fast reliable surrogates for safety critical large scale optimization workloads.

Regularization and Global Optimization in Model-Based Clustering

Due to their conceptual simplicity, k-means algorithm variants have been extensively used for unsupervised cluster analysis. However, one main shortcoming of these algorithms is that they essentially fit a mixture of identical spherical Gaussians to data that vastly deviates from such a distribution. In comparison, general Gaussian Mixture Models (GMMs) can fit richer structures but require estimating a quadratic number of parameters per cluster to represent the covariance matrices. This poses two main issues: (i) the underlying optimization problems are challenging due to their larger number of local minima, and (ii) their solutions can overfit the data. In this work, we design search strategies that circumvent both issues. We develop efficient global optimization algorithms for general GMMs, and we combine these algorithms with regularization strategies that avoid overfitting. Through extensive computational analyses, we observe that global optimization or regularization in isolation does not substantially improve cluster recovery. However, combining these techniques permits a completely new level of performance previously unachieved by k-means algorithm variants, unraveling vastly different cluster structures. These results shed new light on the current status quo between GMM and k-means methods and suggest the more frequent use of general GMMs for data exploration. To facilitate such applications, we provide open-source code as well as Julia packages ("UnsupervisedClustering.jl" and "RegularizedCovarianceMatrices.jl") implementing the proposed techniques.

Flexible Differentiable Optimization via Model Transformations

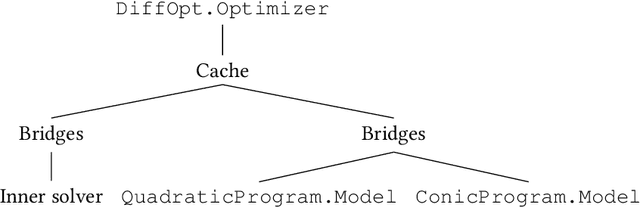
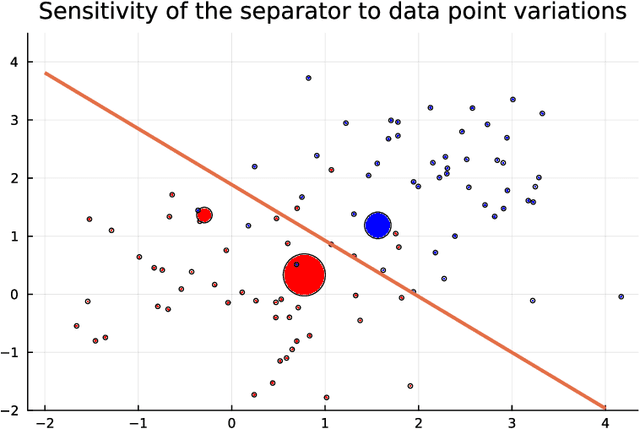
We introduce DiffOpt.jl, a Julia library to differentiate through the solution of convex optimization problems with respect to arbitrary parameters present in the objective and/or constraints. The library builds upon MathOptInterface, thus leveraging the rich ecosystem of solvers and composing well with modelling languages like JuMP. DiffOpt offers both forward and reverse differentiation modes, enabling multiple use cases from hyperparameter optimization to backpropagation and sensitivity analysis, bridging constrained optimization with end-to-end differentiable programming.

Community Detection for Power Systems Network Aggregation Considering Renewable Variability

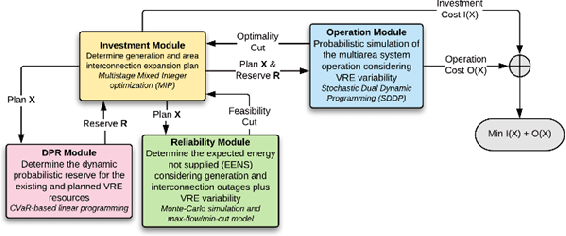
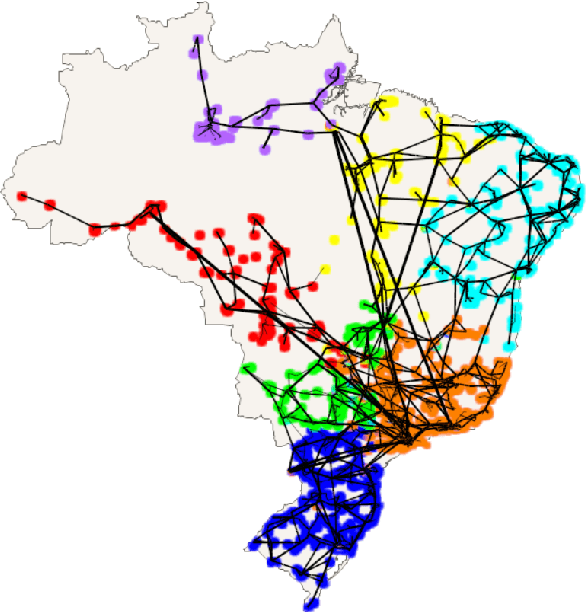
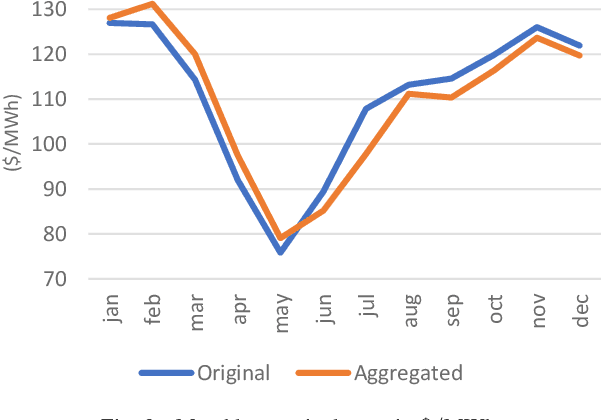
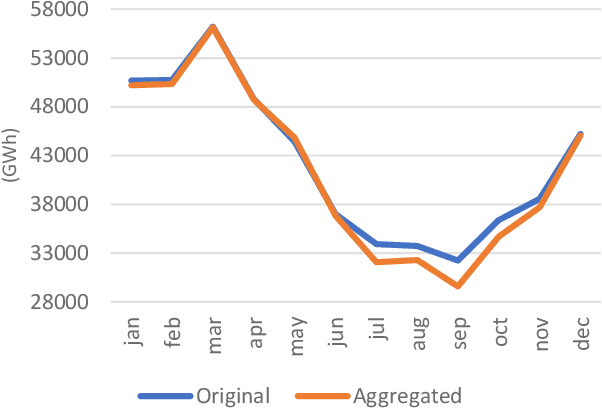
The increasing penetration of variable renewable energy (VRE) has brought significant challenges for power systems planning and operation. These highly variable sources are typically distributed in the grid; therefore, a detailed representation of transmission bottlenecks is fundamental to approximate the impact of the transmission network on the dispatch with VRE resources. The fine grain temporal scale of short term and day-ahead dispatch, taking into account the network constraints, also mandatory for mid-term planning studies, combined with the high variability of the VRE has brought the need to represent these uncertainties in stochastic optimization models while taking into account the transmission system. These requirements impose a computational burden to solve the planning and operation models. We propose a methodology based on community detection to aggregate the network representation, capable of preserving the locational marginal price (LMP) differences in multiple VRE scenarios, and describe a real-world operational planning study. The optimal expected cost solution considering aggregated networks is compared with the full network representation. Both representations were embedded in an operation model relying on Stochastic Dual Dynamic Programming (SDDP) to deal with the random variables in a multi-stage problem.