Benoît Legat
A General and Streamlined Differentiable Optimization Framework
Oct 29, 2025Abstract:Differentiating through constrained optimization problems is increasingly central to learning, control, and large-scale decision-making systems, yet practical integration remains challenging due to solver specialization and interface mismatches. This paper presents a general and streamlined framework-an updated DiffOpt.jl-that unifies modeling and differentiation within the Julia optimization stack. The framework computes forward - and reverse-mode solution and objective sensitivities for smooth, potentially nonconvex programs by differentiating the KKT system under standard regularity assumptions. A first-class, JuMP-native parameter-centric API allows users to declare named parameters and obtain derivatives directly with respect to them - even when a parameter appears in multiple constraints and objectives - eliminating brittle bookkeeping from coefficient-level interfaces. We illustrate these capabilities on convex and nonconvex models, including economic dispatch, mean-variance portfolio selection with conic risk constraints, and nonlinear robot inverse kinematics. Two companion studies further demonstrate impact at scale: gradient-based iterative methods for strategic bidding in energy markets and Sobolev-style training of end-to-end optimization proxies using solver-accurate sensitivities. Together, these results demonstrate that differentiable optimization can be deployed as a routine tool for experimentation, learning, calibration, and design-without deviating from standard JuMP modeling practices and while retaining access to a broad ecosystem of solvers.
Flexible Differentiable Optimization via Model Transformations
Jun 10, 2022
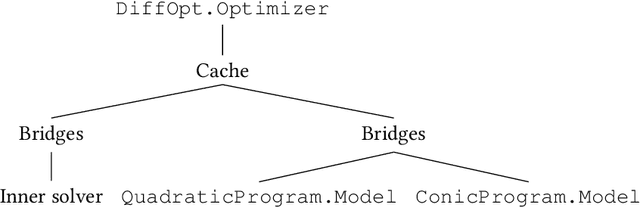

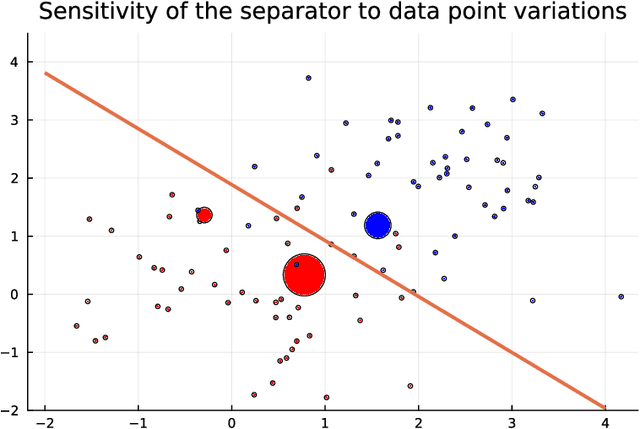
Abstract:We introduce DiffOpt.jl, a Julia library to differentiate through the solution of convex optimization problems with respect to arbitrary parameters present in the objective and/or constraints. The library builds upon MathOptInterface, thus leveraging the rich ecosystem of solvers and composing well with modelling languages like JuMP. DiffOpt offers both forward and reverse differentiation modes, enabling multiple use cases from hyperparameter optimization to backpropagation and sensitivity analysis, bridging constrained optimization with end-to-end differentiable programming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge