LCA-on-the-Line: Benchmarking Out-of-Distribution Generalization with Class Taxonomies

We tackle the challenge of predicting models' Out-of-Distribution (OOD) performance using in-distribution (ID) measurements without requiring OOD data. Existing evaluations with "Effective Robustness", which use ID accuracy as an indicator of OOD accuracy, encounter limitations when models are trained with diverse supervision and distributions, such as class labels (Vision Models, VMs, on ImageNet) and textual descriptions (Visual-Language Models, VLMs, on LAION). VLMs often generalize better to OOD data than VMs despite having similar or lower ID performance. To improve the prediction of models' OOD performance from ID measurements, we introduce the Lowest Common Ancestor (LCA)-on-the-Line framework. This approach revisits the established concept of LCA distance, which measures the hierarchical distance between labels and predictions within a predefined class hierarchy, such as WordNet. We assess 75 models using ImageNet as the ID dataset and five significantly shifted OOD variants, uncovering a strong linear correlation between ID LCA distance and OOD top-1 accuracy. Our method provides a compelling alternative for understanding why VLMs tend to generalize better. Additionally, we propose a technique to construct a taxonomic hierarchy on any dataset using K-means clustering, demonstrating that LCA distance is robust to the constructed taxonomic hierarchy. Moreover, we demonstrate that aligning model predictions with class taxonomies, through soft labels or prompt engineering, can enhance model generalization. Open source code in our Project Page: https://elvishelvis.github.io/papers/lca/.

Contrasting the landscape of contrastive and non-contrastive learning

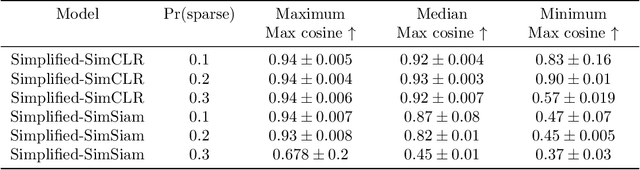
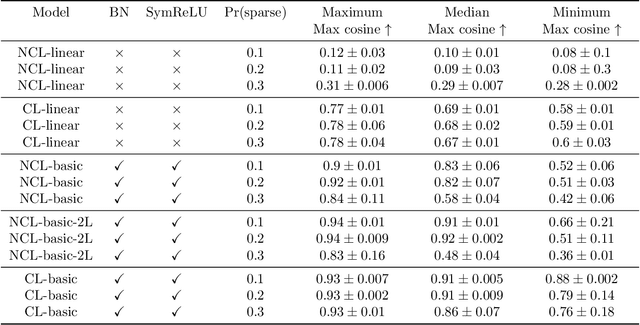
A lot of recent advances in unsupervised feature learning are based on designing features which are invariant under semantic data augmentations. A common way to do this is contrastive learning, which uses positive and negative samples. Some recent works however have shown promising results for non-contrastive learning, which does not require negative samples. However, the non-contrastive losses have obvious "collapsed" minima, in which the encoders output a constant feature embedding, independent of the input. A folk conjecture is that so long as these collapsed solutions are avoided, the produced feature representations should be good. In our paper, we cast doubt on this story: we show through theoretical results and controlled experiments that even on simple data models, non-contrastive losses have a preponderance of non-collapsed bad minima. Moreover, we show that the training process does not avoid these minima.

Online control of the familywise error rate

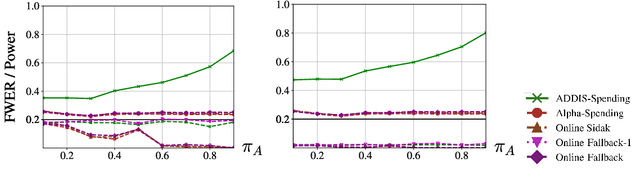
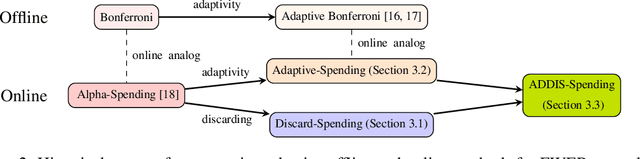
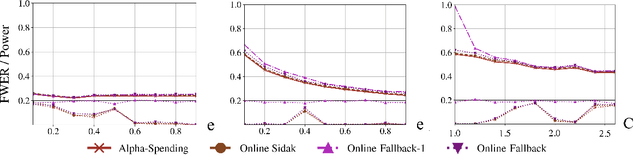
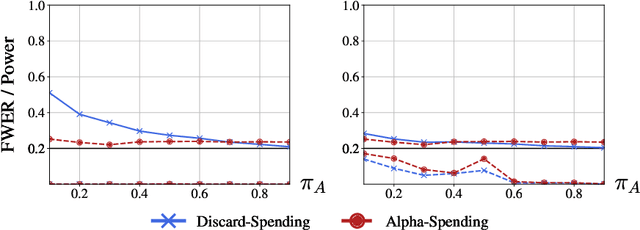
Suppose an analyst wishes to test an infinite sequence of hypotheses one by one over time in such a way that the familywise error rate (FWER) is controlled at level $\alpha$. Specifically, without knowing the future $p$-values, the analyst must irrevocably decide at each step whether to reject the null, such that with probability at least $1-\alpha$, there are no false rejections in the entire sequence. This paper unifies algorithm design concepts developed for offline FWER control and for online false discovery rate (FDR) control. Though Bonferroni, fallback procedures and Sidak's method can trivially be extended to the online setting, our main contribution is the design of new, adaptive online algorithms that control the FWER and per-family error rate (PFER) when the $p$-values are independent or locally dependent in time. Our experiments demonstrate substantial gains in power, also formally proved in an idealized Gaussian model.

ADDIS: an adaptive discarding algorithm for online FDR control with conservative nulls

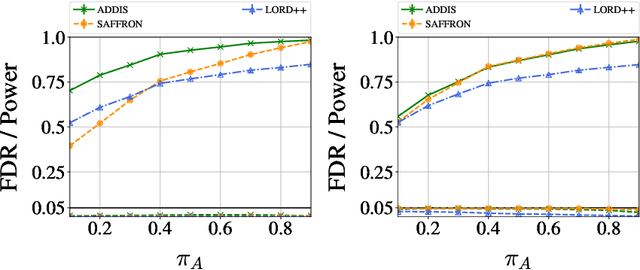
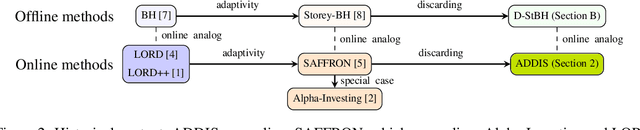
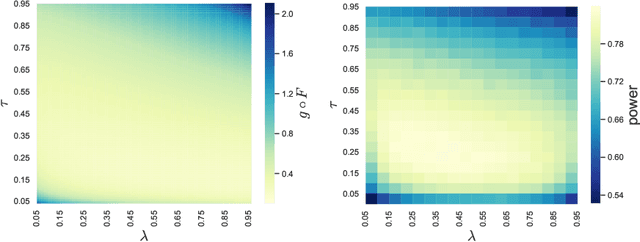
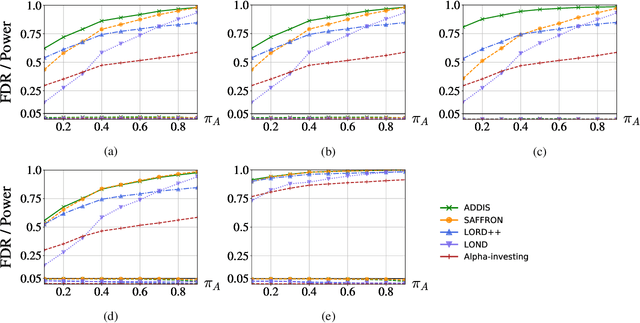
Major internet companies routinely perform tens of thousands of A/B tests each year. Such large-scale sequential experimentation has resulted in a recent spurt of new algorithms that can provably control the false discovery rate (FDR) in a fully online fashion. However, current state-of-the-art adaptive algorithms can suffer from a significant loss in power if null p-values are conservative (stochastically larger than the uniform distribution), a situation that occurs frequently in practice. In this work, we introduce a new adaptive discarding method called ADDIS that provably controls the FDR and achieves the best of both worlds: it enjoys appreciable power increase over all existing methods if nulls are conservative (the practical case), and rarely loses power if nulls are exactly uniformly distributed (the ideal case). We provide several practical insights on robust choices of tuning parameters, and extend the idea to asynchronous and offline settings as well.