Seismic Acoustic Impedance Inversion Framework Based on Conditional Latent Generative Diffusion Model

Seismic acoustic impedance plays a crucial role in lithological identification and subsurface structure interpretation. However, due to the inherently ill-posed nature of the inversion problem, directly estimating impedance from post-stack seismic data remains highly challenging. Recently, diffusion models have shown great potential in addressing such inverse problems due to their strong prior learning and generative capabilities. Nevertheless, most existing methods operate in the pixel domain and require multiple iterations, limiting their applicability to field data. To alleviate these limitations, we propose a novel seismic acoustic impedance inversion framework based on a conditional latent generative diffusion model, where the inversion process is made in latent space. To avoid introducing additional training overhead when embedding conditional inputs, we design a lightweight wavelet-based module into the framework to project seismic data and reuse an encoder trained on impedance to embed low-frequency impedance into the latent space. Furthermore, we propose a model-driven sampling strategy during the inversion process of this framework to enhance accuracy and reduce the number of required diffusion steps. Numerical experiments on a synthetic model demonstrate that the proposed method achieves high inversion accuracy and strong generalization capability within only a few diffusion steps. Moreover, application to field data reveals enhanced geological detail and higher consistency with well-log measurements, validating the effectiveness and practicality of the proposed approach.

High-resolution chirplet transform: from parameters analysis to parameters combination

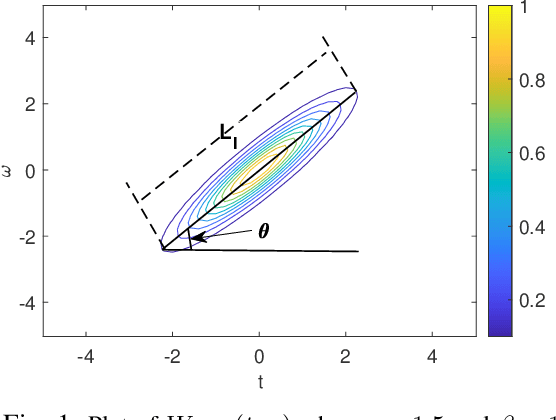
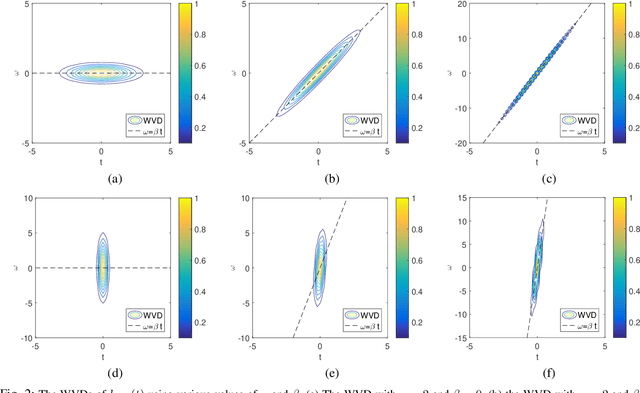
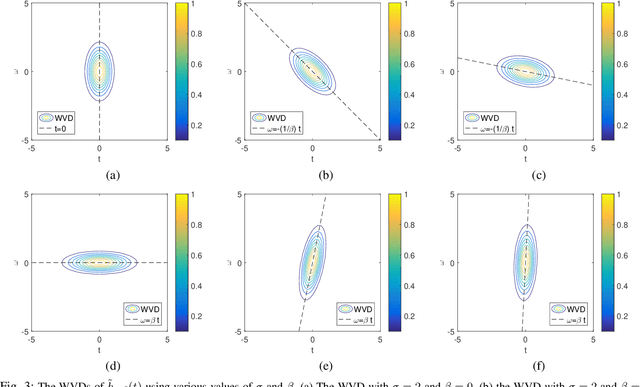
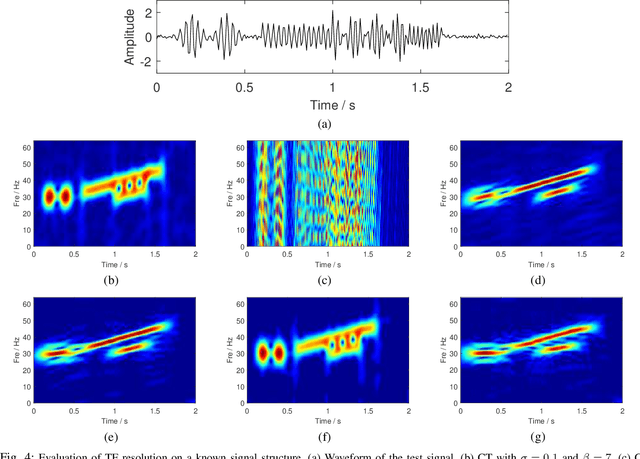
The standard chirplet transform (CT) with a chirp-modulated Gaussian window provides a valuable tool for analyzing linear chirp signals. The parameters present in the window determine the performance of CT and play a very important role in high-resolution time-frequency (TF) analysis. In this paper, we first give the window shape analysis of CT and compare it with the extension that employs a rotating Gaussian window by fractional Fourier transform. The given parameters analysis provides certain theoretical guidance for developing high-resolution CT. We then propose a multi-resolution chirplet transform (MrCT) by combining multiple CTs with different parameter combinations. These are combined geometrically to obtain an improved TF resolution by overcoming the limitations of any single representation of the CT. By deriving the combined instantaneous frequency equation, we further develop a high-concentration TF post-processing approach to improve the readability of the MrCT. Numerical experiments on simulated and real signals verify its effectiveness.