STF-GCN: A Multi-Domain Graph Convolution Network Method for Automatic Modulation Recognition via Adaptive Correlation

Automatic Modulation Recognition (AMR) is an essential part of Intelligent Transportation System (ITS) dynamic spectrum allocation. However, current deep learning-based AMR (DL-AMR) methods are challenged to extract discriminative and robust features at low signal-to-noise ratios (SNRs), where the representation of modulation symbols is highly interfered by noise. Furthermore, current research on GNN methods for AMR tasks generally suffers from issues related to graph structure construction and computational complexity. In this paper, we propose a Spatial-Temporal-Frequency Graph Convolution Network (STF-GCN) framework, with the temporal domain as the anchor point, to fuse spatial and frequency domain features embedded in the graph structure nodes. On this basis, an adaptive correlation-based adjacency matrix construction method is proposed, which significantly enhances the graph structure's capacity to aggregate local information into individual nodes. In addition, a PoolGAT layer is proposed to coarsen and compress the global key features of the graph, significantly reducing the computational complexity. The results of the experiments confirm that STF-GCN is able to achieve recognition performance far beyond the state-of-the-art DL-AMR algorithms, with overall accuracies of 64.35%, 66.04% and 70.95% on the RML2016.10a, RML2016.10b and RML22 datasets, respectively. Furthermore, the average recognition accuracies under low SNR conditions from -14dB to 0dB outperform the state-of-the-art (SOTA) models by 1.20%, 1.95% and 1.83%, respectively.

Neural Operator based Reinforcement Learning for Control of first-order PDEs with Spatially-Varying State Delay

Control of distributed parameter systems affected by delays is a challenging task, particularly when the delays depend on spatial variables. The idea of integrating analytical control theory with learning-based control within a unified control scheme is becoming increasingly promising and advantageous. In this paper, we address the problem of controlling an unstable first-order hyperbolic PDE with spatially-varying delays by combining PDE backstepping control strategies and deep reinforcement learning (RL). To eliminate the assumption on the delay function required for the backstepping design, we propose a soft actor-critic (SAC) architecture incorporating a DeepONet to approximate the backstepping controller. The DeepONet extracts features from the backstepping controller and feeds them into the policy network. In simulations, our algorithm outperforms the baseline SAC without prior backstepping knowledge and the analytical controller.

Adaptive Line-Of-Sight guidance law based on vector fields path following for underactuated unmanned surface vehicle

The focus of this paper is to develop a methodology that enables an unmanned surface vehicle (USV) to efficiently track a planned path. The introduction of a vector field-based adaptive line of-sight guidance law (VFALOS) for accurate trajectory tracking and minimizing the overshoot response time during USV tracking of curved paths improves the overall line-of-sight (LOS) guidance method. These improvements contribute to faster convergence to the desired path, reduce oscillations, and can mitigate the effects of persistent external disturbances. It is shown that the proposed guidance law exhibits k-exponential stability when converging to the desired path consisting of straight and curved lines. The results in the paper show that the proposed method effectively improves the accuracy of the USV tracking the desired path while ensuring the safety of the USV work.

Neural Operators for Delay-Compensating Control of Hyperbolic PIDEs

The recently introduced DeepONet operator-learning framework for PDE control is extended from the results for basic hyperbolic and parabolic PDEs to an advanced hyperbolic class that involves delays on both the state and the system output or input. The PDE backstepping design produces gain functions that are outputs of a nonlinear operator, mapping functions on a spatial domain into functions on a spatial domain, and where this gain-generating operator's inputs are the PDE's coefficients. The operator is approximated with a DeepONet neural network to a degree of accuracy that is provably arbitrarily tight. Once we produce this approximation-theoretic result in infinite dimension, with it we establish stability in closed loop under feedback that employs approximate gains. In addition to supplying such results under full-state feedback, we also develop DeepONet-approximated observers and output-feedback laws and prove their own stabilizing properties under neural operator approximations. With numerical simulations we illustrate the theoretical results and quantify the numerical effort savings, which are of two orders of magnitude, thanks to replacing the numerical PDE solving with the DeepONet.

Proximal Policy Optimization Learning based Control of Congested Freeway Traffic

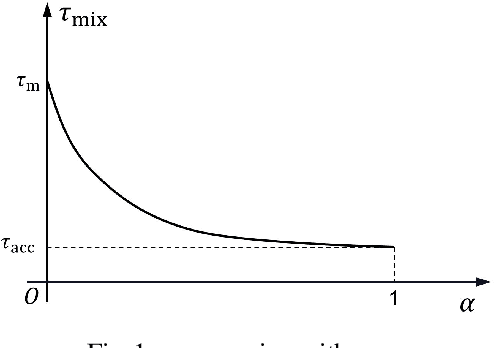
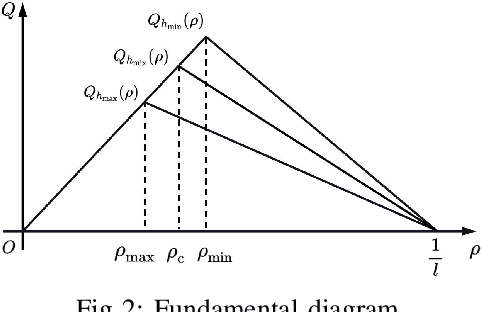
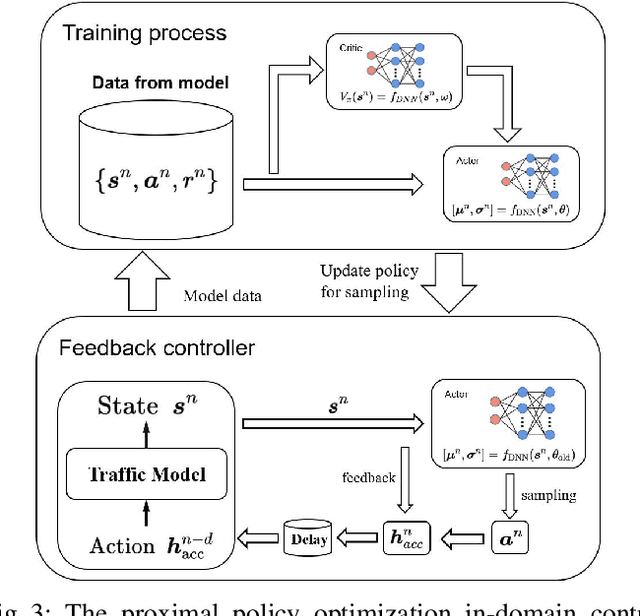
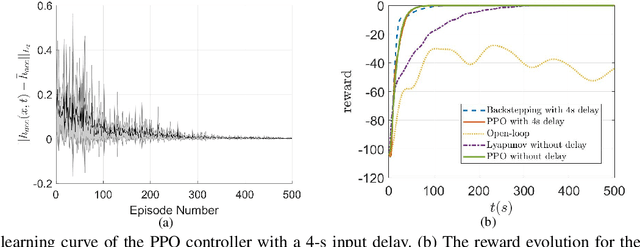
This study proposes a delay-compensated feedback controller based on proximal policy optimization (PPO) reinforcement learning to stabilize traffic flow in the congested regime by manipulating the time-gap of adaptive cruise control-equipped (ACC-equipped) vehicles.The traffic dynamics on a freeway segment are governed by an Aw-Rascle-Zhang (ARZ) model, consisting of $2\times 2$ nonlinear first-order partial differential equations (PDEs).Inspired by the backstepping delay compensator [18] but different from whose complex segmented control scheme, the PPO control is composed of three feedbacks, namely the current traffic flow velocity, the current traffic flow density and previous one step control input. The control gains for the three feedbacks are learned from the interaction between the PPO and the numerical simulator of the traffic system without knowing the system dynamics. Numerical simulation experiments are designed to compare the Lyapunov control, the backstepping control and the PPO control. The results show that for a delay-free system, the PPO control has faster convergence rate and less control effort than the Lyapunov control. For a traffic system with input delay, the performance of the PPO controller is comparable to that of the Backstepping controller, even for the situation that the delay value does not match. However, the PPO is robust to parameter perturbations, while the Backstepping controller cannot stabilize a system where one of the parameters is disturbed by Gaussian noise.