CloSE: A Compact Shape- and Orientation-Agnostic Cloth State Representation

Cloth manipulation is a difficult problem mainly because of the non-rigid nature of cloth, which makes a good representation of deformation essential. We present a new representation for the deformation-state of clothes. First, we propose the dGLI disk representation, based on topological indices computed for segments on the edges of the cloth mesh border that are arranged on a circular grid. The heat-map of the dGLI disk uncovers patterns that correspond to features of the cloth state that are consistent for different shapes, sizes of positions of the cloth, like the corners and the fold locations. We then abstract these important features from the dGLI disk onto a circle, calling it the Cloth StatE representation (CloSE). This representation is compact, continuous, and general for different shapes. Finally, we show the strengths of this representation in two relevant applications: semantic labeling and high- and low-level planning. The code, the dataset and the video can be accessed from : https://jaykamat99.github.io/close-representation

BITKOMO: Combining Sampling and Optimization for Fast Convergence in Optimal Motion Planning

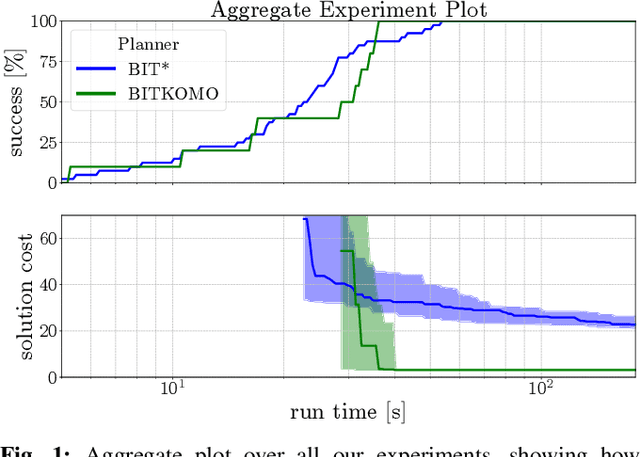
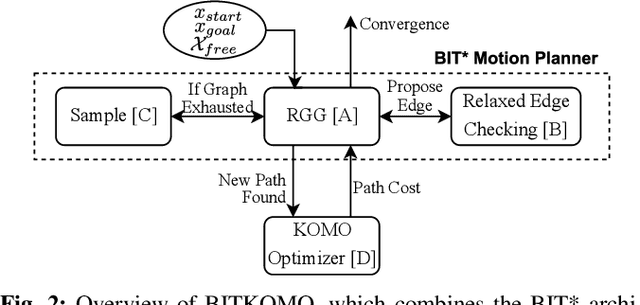
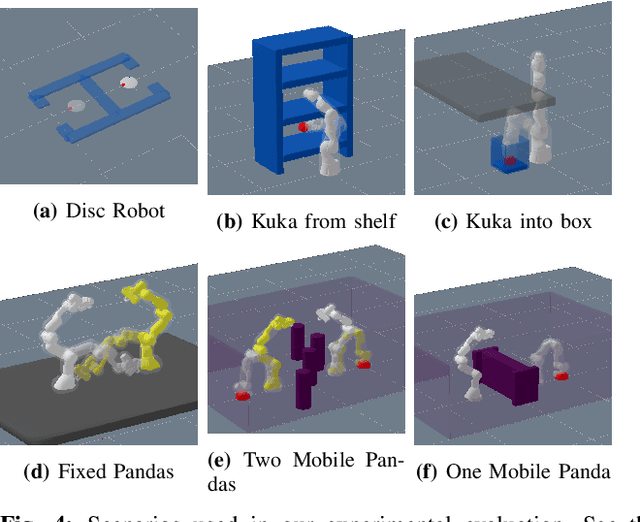
Optimal sampling based motion planning and trajectory optimization are two competing frameworks to generate optimal motion plans. Both frameworks have complementary properties: Sampling based planners are typically slow to converge, but provide optimality guarantees. Trajectory optimizers, however, are typically fast to converge, but do not provide global optimality guarantees in nonconvex problems, e.g. scenarios with obstacles. To achieve the best of both worlds, we introduce a new planner, BITKOMO, which integrates the asymptotically optimal Batch Informed Trees (BIT*) planner with the K-Order Markov Optimization (KOMO) trajectory optimization framework. Our planner is anytime and maintains the same asymptotic optimality guarantees provided by BIT*, while also exploiting the fast convergence of the KOMO trajectory optimizer. We experimentally evaluate our planner on manipulation scenarios that involve high dimensional configuration spaces, with up to two 7-DoF manipulators, obstacles and narrow passages. BITKOMO performs better than KOMO by succeeding even when KOMO fails, and it outperforms BIT* in terms of convergence to the optimal solution.