Inferring response times of perceptual decisions with Poisson variational autoencoders

Many properties of perceptual decision making are well-modeled by deep neural networks. However, such architectures typically treat decisions as instantaneous readouts, overlooking the temporal dynamics of the decision process. We present an image-computable model of perceptual decision making in which choices and response times arise from efficient sensory encoding and Bayesian decoding of neural spiking activity. We use a Poisson variational autoencoder to learn unsupervised representations of visual stimuli in a population of rate-coded neurons, modeled as independent homogeneous Poisson processes. A task-optimized decoder then continually infers an approximate posterior over actions conditioned on incoming spiking activity. Combining these components with an entropy-based stopping rule yields a principled and image-computable model of perceptual decisions capable of generating trial-by-trial patterns of choices and response times. Applied to MNIST digit classification, the model reproduces key empirical signatures of perceptual decision making, including stochastic variability, right-skewed response time distributions, logarithmic scaling of response times with the number of alternatives (Hick's law), and speed-accuracy trade-offs.

A prescriptive theory for brain-like inference

The Evidence Lower Bound (ELBO) is a widely used objective for training deep generative models, such as Variational Autoencoders (VAEs). In the neuroscience literature, an identical objective is known as the variational free energy, hinting at a potential unified framework for brain function and machine learning. Despite its utility in interpreting generative models, including diffusion models, ELBO maximization is often seen as too broad to offer prescriptive guidance for specific architectures in neuroscience or machine learning. In this work, we show that maximizing ELBO under Poisson assumptions for general sequence data leads to a spiking neural network that performs Bayesian posterior inference through its membrane potential dynamics. The resulting model, the iterative Poisson VAE (iP-VAE), has a closer connection to biological neurons than previous brain-inspired predictive coding models based on Gaussian assumptions. Compared to amortized and iterative VAEs, iP-VAElearns sparser representations and exhibits superior generalization to out-of-distribution samples. These findings suggest that optimizing ELBO, combined with Poisson assumptions, provides a solid foundation for developing prescriptive theories in NeuroAI.

Poisson Variational Autoencoder

Variational autoencoders (VAE) employ Bayesian inference to interpret sensory inputs, mirroring processes that occur in primate vision across both ventral (Higgins et al., 2021) and dorsal (Vafaii et al., 2023) pathways. Despite their success, traditional VAEs rely on continuous latent variables, which deviates sharply from the discrete nature of biological neurons. Here, we developed the Poisson VAE (P-VAE), a novel architecture that combines principles of predictive coding with a VAE that encodes inputs into discrete spike counts. Combining Poisson-distributed latent variables with predictive coding introduces a metabolic cost term in the model loss function, suggesting a relationship with sparse coding which we verify empirically. Additionally, we analyze the geometry of learned representations, contrasting the P-VAE to alternative VAE models. We find that the P-VAEencodes its inputs in relatively higher dimensions, facilitating linear separability of categories in a downstream classification task with a much better (5x) sample efficiency. Our work provides an interpretable computational framework to study brain-like sensory processing and paves the way for a deeper understanding of perception as an inferential process.

Efficient non-conjugate Gaussian process factor models for spike count data using polynomial approximations

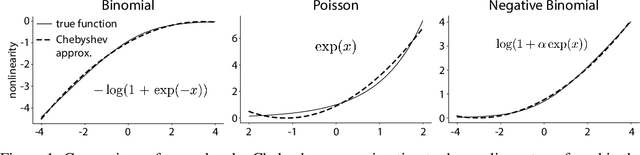
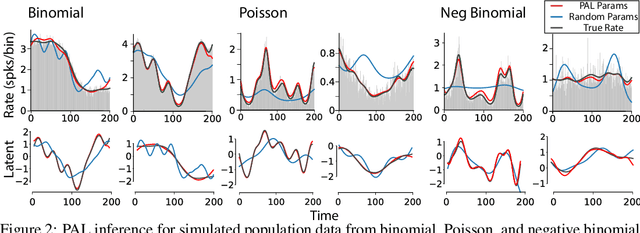
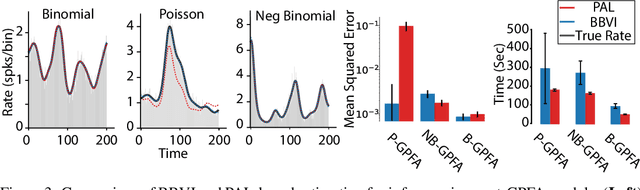
Gaussian Process Factor Analysis (GPFA) has been broadly applied to the problem of identifying smooth, low-dimensional temporal structure underlying large-scale neural recordings. However, spike trains are non-Gaussian, which motivates combining GPFA with discrete observation models for binned spike count data. The drawback to this approach is that GPFA priors are not conjugate to count model likelihoods, which makes inference challenging. Here we address this obstacle by introducing a fast, approximate inference method for non-conjugate GPFA models. Our approach uses orthogonal second-order polynomials to approximate the nonlinear terms in the non-conjugate log-likelihood, resulting in a method we refer to as polynomial approximate log-likelihood (PAL) estimators. This approximation allows for accurate closed-form evaluation of marginal likelihood and fast numerical optimization for parameters and hyperparameters. We derive PAL estimators for GPFA models with binomial, Poisson, and negative binomial observations, and additionally show that the parameters obtained can be used to initialize black-box variational inference, which significantly speeds up and stabilizes the inference procedure for these factor analytic models. We apply these methods to data from mouse visual cortex and monkey higher-order visual and parietal cortices, and compare GPFA under three different spike count observation models to traditional GPFA. We demonstrate that PAL estimators achieve fast and accurate extraction of latent structure from multi-neuron spike train data.