Spatially relaxed inference on high-dimensional linear models

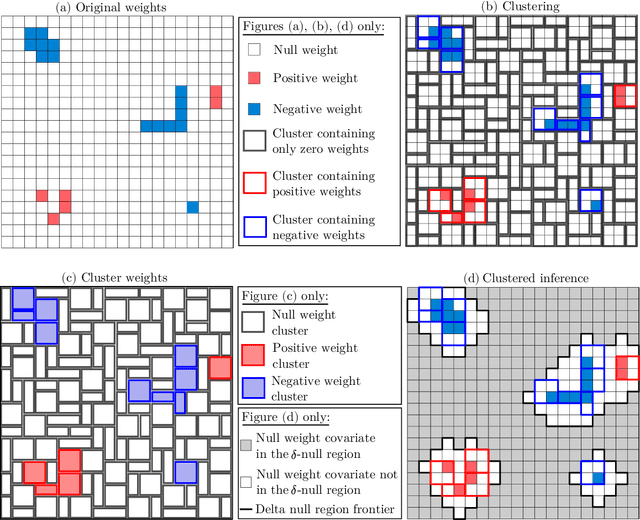
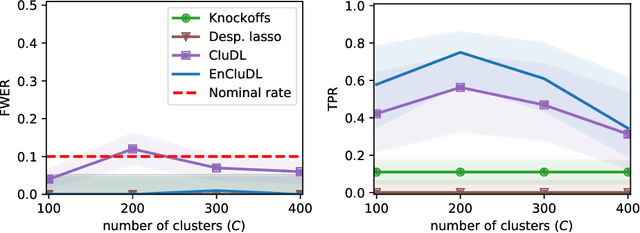
We consider the inference problem for high-dimensional linear models, when covariates have an underlying spatial organization reflected in their correlation. A typical example of such a setting is high-resolution imaging, in which neighboring pixels are usually very similar. Accurate point and confidence intervals estimation is not possible in this context with many more covariates than samples, furthermore with high correlation between covariates. This calls for a reformulation of the statistical inference problem, that takes into account the underlying spatial structure: if covariates are locally correlated, it is acceptable to detect them up to a given spatial uncertainty. We thus propose to rely on the $\delta$-FWER, that is the probability of making a false discovery at a distance greater than $\delta$ from any true positive. With this target measure in mind, we study the properties of ensembled clustered inference algorithms which combine three techniques: spatially constrained clustering, statistical inference, and ensembling to aggregate several clustered inference solutions. We show that ensembled clustered inference algorithms control the $\delta$-FWER under standard assumptions for $\delta$ equal to the largest cluster diameter. We complement the theoretical analysis with empirical results, demonstrating accurate $\delta$-FWER control and decent power achieved by such inference algorithms.

Statistical control for spatio-temporal MEG/EEG source imaging with desparsified multi-task Lasso

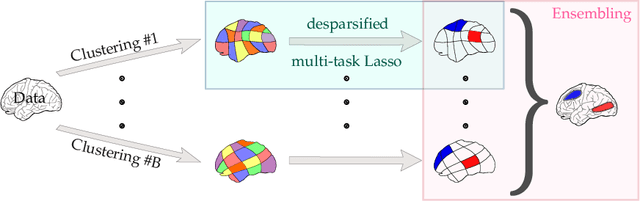
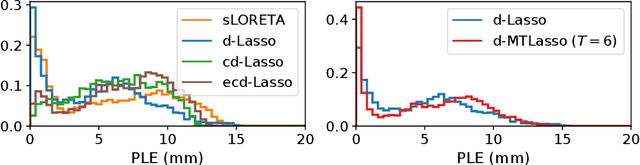
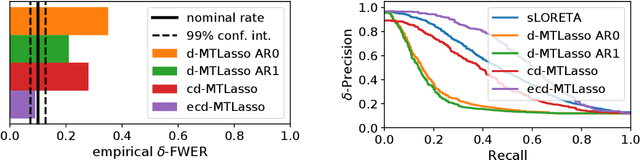
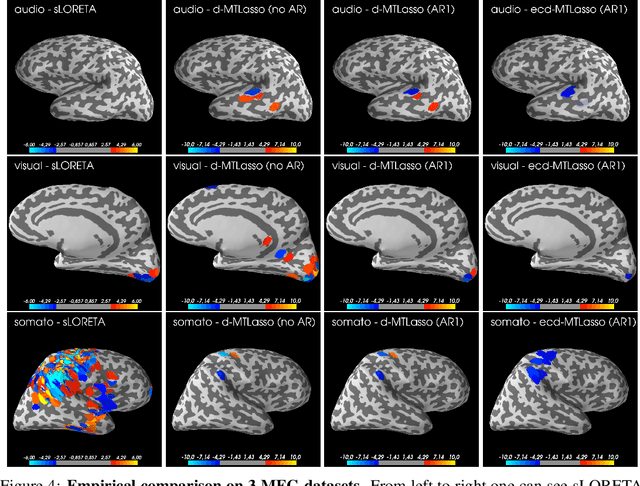
Detecting where and when brain regions activate in a cognitive task or in a given clinical condition is the promise of non-invasive techniques like magnetoencephalography (MEG) or electroencephalography (EEG). This problem, referred to as source localization, or source imaging, poses however a high-dimensional statistical inference challenge. While sparsity promoting regularizations have been proposed to address the regression problem, it remains unclear how to ensure statistical control of false detections. Moreover, M/EEG source imaging requires to work with spatio-temporal data and autocorrelated noise. To deal with this, we adapt the desparsified Lasso estimator -- an estimator tailored for high dimensional linear model that asymptotically follows a Gaussian distribution under sparsity and moderate feature correlation assumptions -- to temporal data corrupted with autocorrelated noise. We call it the desparsified multi-task Lasso (d-MTLasso). We combine d-MTLasso with spatially constrained clustering to reduce data dimension and with ensembling to mitigate the arbitrary choice of clustering; the resulting estimator is called ensemble of clustered desparsified multi-task Lasso (ecd-MTLasso). With respect to the current procedures, the two advantages of ecd-MTLasso are that i)it offers statistical guarantees and ii)it allows to trade spatial specificity for sensitivity, leading to a powerful adaptive method. Extensive simulations on realistic head geometries, as well as empirical results on various MEG datasets, demonstrate the high recovery performance of ecd-MTLasso and its primary practical benefit: offer a statistically principled way to threshold MEG/EEG source maps.

Aggregation of Multiple Knockoffs

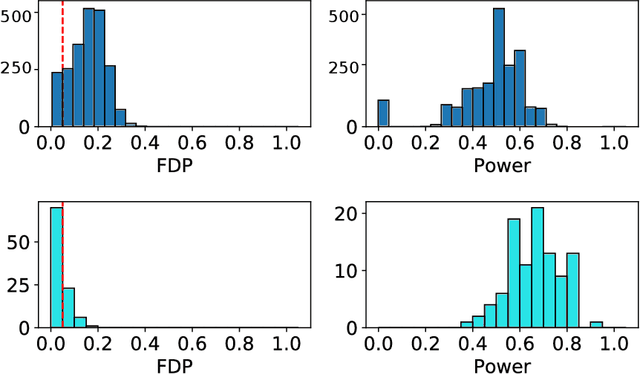
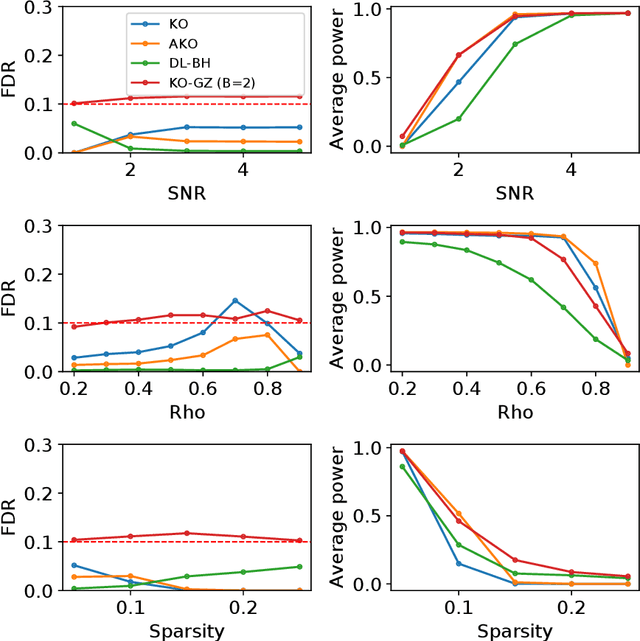
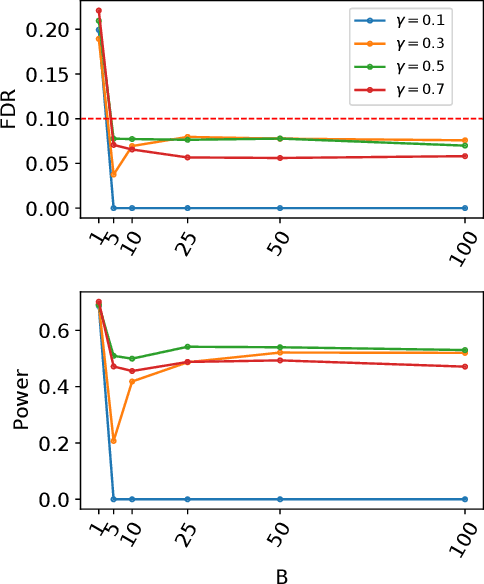
We develop an extension of the Knockoff Inference procedure, introduced by Barber and Candes (2015). This new method, called Aggregation of Multiple Knockoffs (AKO), addresses the instability inherent to the random nature of Knockoff-based inference. Specifically, AKO improves both the stability and power compared with the original Knockoff algorithm while still maintaining guarantees for False Discovery Rate control. We provide a new inference procedure, prove its core properties, and demonstrate its benefits in a set of experiments on synthetic and real datasets.