MALT Powers Up Adversarial Attacks

Current adversarial attacks for multi-class classifiers choose the target class for a given input naively, based on the classifier's confidence levels for various target classes. We present a novel adversarial targeting method, \textit{MALT - Mesoscopic Almost Linearity Targeting}, based on medium-scale almost linearity assumptions. Our attack wins over the current state of the art AutoAttack on the standard benchmark datasets CIFAR-100 and ImageNet and for a variety of robust models. In particular, our attack is \emph{five times faster} than AutoAttack, while successfully matching all of AutoAttack's successes and attacking additional samples that were previously out of reach. We then prove formally and demonstrate empirically that our targeting method, although inspired by linear predictors, also applies to standard non-linear models.

Polynomial Time Cryptanalytic Extraction of Neural Network Models

Billions of dollars and countless GPU hours are currently spent on training Deep Neural Networks (DNNs) for a variety of tasks. Thus, it is essential to determine the difficulty of extracting all the parameters of such neural networks when given access to their black-box implementations. Many versions of this problem have been studied over the last 30 years, and the best current attack on ReLU-based deep neural networks was presented at Crypto 2020 by Carlini, Jagielski, and Mironov. It resembles a differential chosen plaintext attack on a cryptosystem, which has a secret key embedded in its black-box implementation and requires a polynomial number of queries but an exponential amount of time (as a function of the number of neurons). In this paper, we improve this attack by developing several new techniques that enable us to extract with arbitrarily high precision all the real-valued parameters of a ReLU-based DNN using a polynomial number of queries and a polynomial amount of time. We demonstrate its practical efficiency by applying it to a full-sized neural network for classifying the CIFAR10 dataset, which has 3072 inputs, 8 hidden layers with 256 neurons each, and over million neuronal parameters. An attack following the approach by Carlini et al. requires an exhaustive search over 2 to the power 256 possibilities. Our attack replaces this with our new techniques, which require only 30 minutes on a 256-core computer.

Facial Misrecognition Systems: Simple Weight Manipulations Force DNNs to Err Only on Specific Persons

In this paper we describe how to plant novel types of backdoors in any facial recognition model based on the popular architecture of deep Siamese neural networks, by mathematically changing a small fraction of its weights (i.e., without using any additional training or optimization). These backdoors force the system to err only on specific persons which are preselected by the attacker. For example, we show how such a backdoored system can take any two images of a particular person and decide that they represent different persons (an anonymity attack), or take any two images of a particular pair of persons and decide that they represent the same person (a confusion attack), with almost no effect on the correctness of its decisions for other persons. Uniquely, we show that multiple backdoors can be independently installed by multiple attackers who may not be aware of each other's existence with almost no interference. We have experimentally verified the attacks on a FaceNet-based facial recognition system, which achieves SOTA accuracy on the standard LFW dataset of $99.35\%$. When we tried to individually anonymize ten celebrities, the network failed to recognize two of their images as being the same person in $96.97\%$ to $98.29\%$ of the time. When we tried to confuse between the extremely different looking Morgan Freeman and Scarlett Johansson, for example, their images were declared to be the same person in $91.51 \%$ of the time. For each type of backdoor, we sequentially installed multiple backdoors with minimal effect on the performance of each one (for example, anonymizing all ten celebrities on the same model reduced the success rate for each celebrity by no more than $0.91\%$). In all of our experiments, the benign accuracy of the network on other persons was degraded by no more than $0.48\%$ (and in most cases, it remained above $99.30\%$).

The Dimpled Manifold Model of Adversarial Examples in Machine Learning

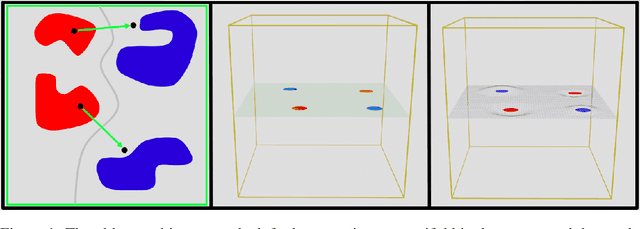
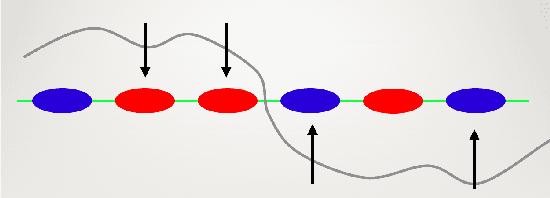
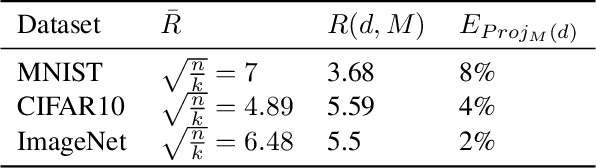
The extreme fragility of deep neural networks when presented with tiny perturbations in their inputs was independently discovered by several research groups in 2013, but in spite of enormous effort these adversarial examples remained a baffling phenomenon with no clear explanation. In this paper we introduce a new conceptual framework (which we call the Dimpled Manifold Model) which provides a simple explanation for why adversarial examples exist, why their perturbations have such tiny norms, why these perturbations look like random noise, and why a network which was adversarially trained with incorrectly labeled images can still correctly classify test images. In the last part of the paper we describe the results of numerous experiments which strongly support this new model, and in particular our assertion that adversarial perturbations are roughly perpendicular to the low dimensional manifold which contains all the training examples.

A Simple Explanation for the Existence of Adversarial Examples with Small Hamming Distance

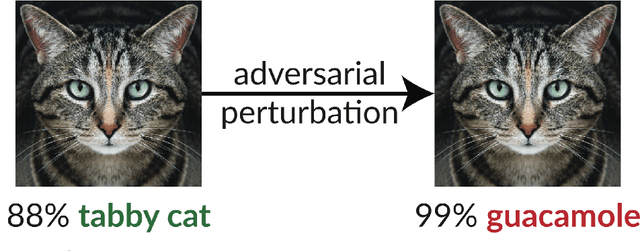
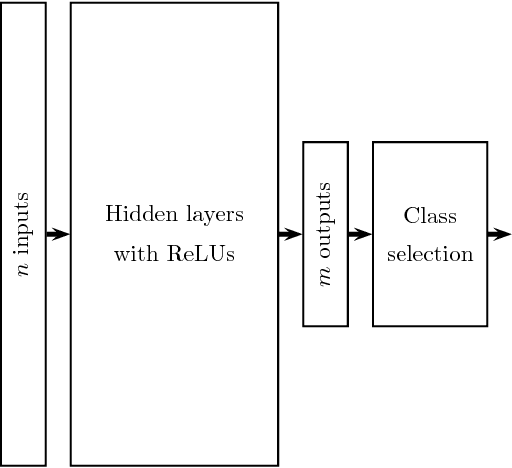
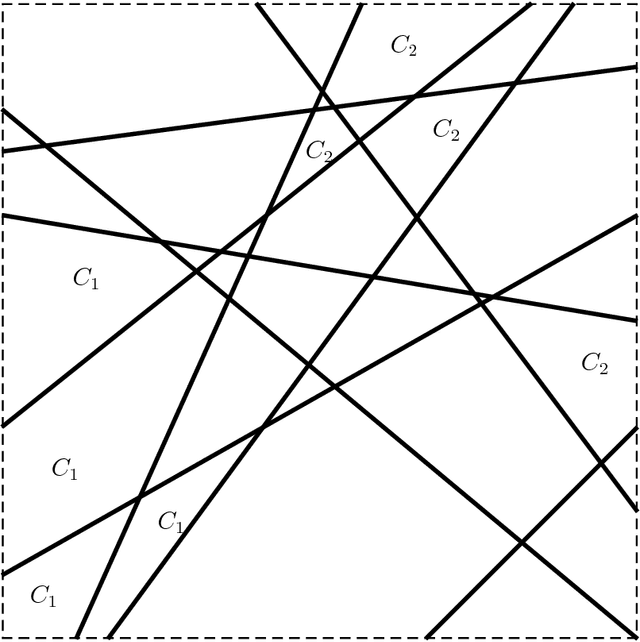
The existence of adversarial examples in which an imperceptible change in the input can fool well trained neural networks was experimentally discovered by Szegedy et al in 2013, who called them "Intriguing properties of neural networks". Since then, this topic had become one of the hottest research areas within machine learning, but the ease with which we can switch between any two decisions in targeted attacks is still far from being understood, and in particular it is not clear which parameters determine the number of input coordinates we have to change in order to mislead the network. In this paper we develop a simple mathematical framework which enables us to think about this baffling phenomenon from a fresh perspective, turning it into a natural consequence of the geometry of $\mathbb{R}^n$ with the $L_0$ (Hamming) metric, which can be quantitatively analyzed. In particular, we explain why we should expect to find targeted adversarial examples with Hamming distance of roughly $m$ in arbitrarily deep neural networks which are designed to distinguish between $m$ input classes.