Linear Convergence of Diffusion Models Under the Manifold Hypothesis

Score-matching generative models have proven successful at sampling from complex high-dimensional data distributions. In many applications, this distribution is believed to concentrate on a much lower $d$-dimensional manifold embedded into $D$-dimensional space; this is known as the manifold hypothesis. The current best-known convergence guarantees are either linear in $D$ or polynomial (superlinear) in $d$. The latter exploits a novel integration scheme for the backward SDE. We take the best of both worlds and show that the number of steps diffusion models require in order to converge in Kullback-Leibler~(KL) divergence is linear (up to logarithmic terms) in the intrinsic dimension $d$. Moreover, we show that this linear dependency is sharp.

Convergence of Diffusion Models Under the Manifold Hypothesis in High-Dimensions

Denoising Diffusion Probabilistic Models (DDPM) are powerful state-of-the-art methods used to generate synthetic data from high-dimensional data distributions and are widely used for image, audio and video generation as well as many more applications in science and beyond. The manifold hypothesis states that high-dimensional data often lie on lower-dimensional manifolds within the ambient space, and is widely believed to hold in provided examples. While recent results has provided invaluable insight into how diffusion models adapt to the manifold hypothesis, they do not capture the great empirical success of these models, making this a very fruitful research direction. In this work, we study DDPMs under the manifold hypothesis and prove that they achieve rates independent of the ambient dimension in terms of learning the score. In terms of sampling, we obtain rates independent of the ambient dimension w.r.t. the Kullback-Leibler divergence, and $O(\sqrt{D})$ w.r.t. the Wasserstein distance. We do this by developing a new framework connecting diffusion models to the well-studied theory of extrema of Gaussian Processes.

The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs

Kernels are a fundamental technical primitive in machine learning. In recent years, kernel-based methods such as Gaussian processes are becoming increasingly important in applications where quantifying uncertainty is of key interest. In settings that involve structured data defined on graphs, meshes, manifolds, or other related spaces, defining kernels with good uncertainty-quantification behavior, and computing their value numerically, is less straightforward than in the Euclidean setting. To address this difficulty, we present GeometricKernels, a software package which implements the geometric analogs of classical Euclidean squared exponential - also known as heat - and Mat\'ern kernels, which are widely-used in settings where uncertainty is of key interest. As a byproduct, we obtain the ability to compute Fourier-feature-type expansions, which are widely used in their own right, on a wide set of geometric spaces. Our implementation supports automatic differentiation in every major current framework simultaneously via a backend-agnostic design. In this companion paper to the package and its documentation, we outline the capabilities of the package and present an illustrated example of its interface. We also include a brief overview of the theory the package is built upon and provide some historic context in the appendix.

Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces II: non-compact symmetric spaces

Gaussian processes are arguably the most important class of spatiotemporal models within machine learning. They encode prior information about the modeled function and can be used for exact or approximate Bayesian learning. In many applications, particularly in physical sciences and engineering, but also in areas such as geostatistics and neuroscience, invariance to symmetries is one of the most fundamental forms of prior information one can consider. The invariance of a Gaussian process' covariance to such symmetries gives rise to the most natural generalization of the concept of stationarity to such spaces. In this work, we develop constructive and practical techniques for building stationary Gaussian processes on a very large class of non-Euclidean spaces arising in the context of symmetries. Our techniques make it possible to (i) calculate covariance kernels and (ii) sample from prior and posterior Gaussian processes defined on such spaces, both in a practical manner. This work is split into two parts, each involving different technical considerations: part I studies compact spaces, while part II studies non-compact spaces possessing certain structure. Our contributions make the non-Euclidean Gaussian process models we study compatible with well-understood computational techniques available in standard Gaussian process software packages, thereby making them accessible to practitioners.

On power sum kernels on symmetric groups

In this note, we introduce a family of "power sum" kernels and the corresponding Gaussian processes on symmetric groups $\mathrm{S}_n$. Such processes are bi-invariant: the action of $\mathrm{S}_n$ on itself from both sides does not change their finite-dimensional distributions. We show that the values of power sum kernels can be efficiently calculated, and we also propose a method enabling approximate sampling of the corresponding Gaussian processes with polynomial computational complexity. By doing this we provide the tools that are required to use the introduced family of kernels and the respective processes for statistical modeling and machine learning.

Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I: the Compact Case

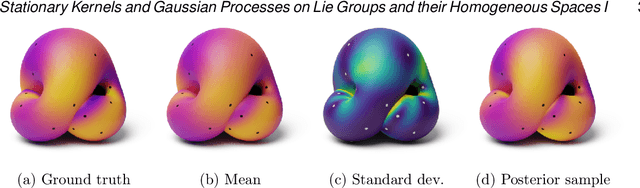
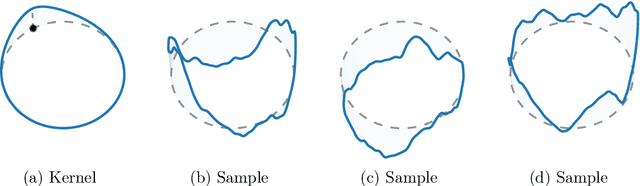
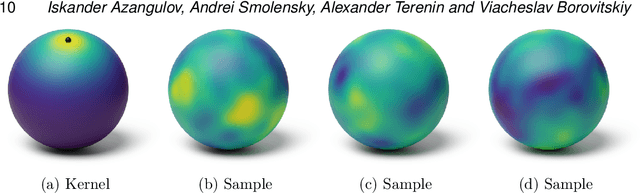
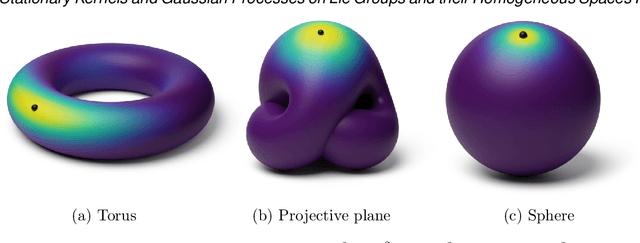
Gaussian processes are arguably the most important model class in spatial statistics. They encode prior information about the modeled function and can be used for exact or approximate Bayesian inference. In many applications, particularly in physical sciences and engineering, but also in areas such as geostatistics and neuroscience, invariance to symmetries is one of the most fundamental forms of prior information one can consider. The invariance of a Gaussian process' covariance to such symmetries gives rise to the most natural generalization of the concept of stationarity to such spaces. In this work, we develop constructive and practical techniques for building stationary Gaussian processes on a very large class of non-Euclidean spaces arising in the context of symmetries. Our techniques make it possible to (i) calculate covariance kernels and (ii) sample from prior and posterior Gaussian processes defined on such spaces, both in a practical manner. This work is split into two parts, each involving different technical considerations: part I studies compact spaces, while part II studies non-compact spaces possessing certain structure. Our contributions make the non-Euclidean Gaussian process models we study compatible with well-understood computational techniques available in standard Gaussian process software packages, thereby making them accessible to practitioners.

Matern Gaussian Processes on Graphs

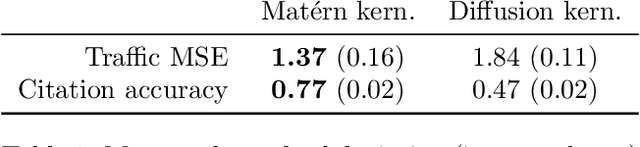
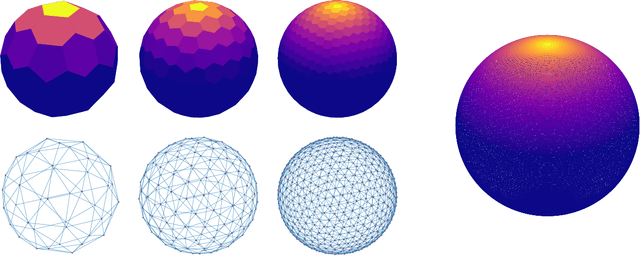
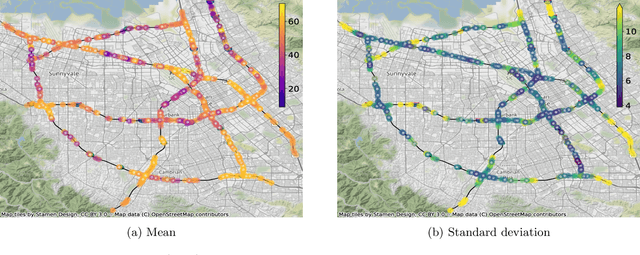
Gaussian processes are a versatile framework for learning unknown functions in a manner that permits one to utilize prior information about their properties. Although many different Gaussian process models are readily available when the input space is Euclidean, the choice is much more limited for Gaussian processes whose input space is an undirected graph. In this work, we leverage the stochastic partial differential equation characterization of Mat\'{e}rn Gaussian processes - a widely-used model class in the Euclidean setting - to study their analog for undirected graphs. We show that the resulting Gaussian processes inherit various attractive properties of their Euclidean and Riemannian analogs and provide techniques that allow them to be trained using standard methods, such as inducing points. This enables graph Mat\'{e}rn Gaussian processes to be employed in mini-batch and non-conjugate settings, thereby making them more accessible to practitioners and easier to deploy within larger learning frameworks.