Irina Cristali
Using Embeddings for Causal Estimation of Peer Influence in Social Networks
May 17, 2022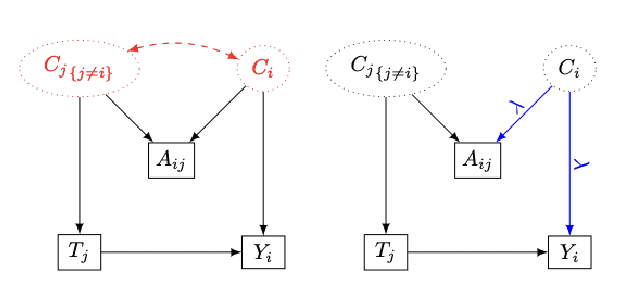
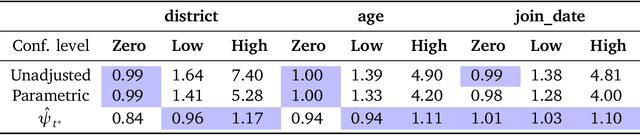

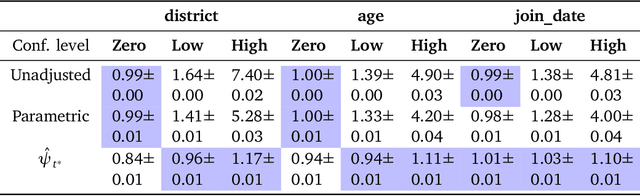
Abstract:We address the problem of using observational data to estimate peer contagion effects, the influence of treatments applied to individuals in a network on the outcomes of their neighbors. A main challenge to such estimation is that homophily - the tendency of connected units to share similar latent traits - acts as an unobserved confounder for contagion effects. Informally, it's hard to tell whether your friends have similar outcomes because they were influenced by your treatment, or whether it's due to some common trait that caused you to be friends in the first place. Because these common causes are not usually directly observed, they cannot be simply adjusted for. We describe an approach to perform the required adjustment using node embeddings learned from the network itself. The main aim is to perform this adjustment nonparametrically, without functional form assumptions on either the process that generated the network or the treatment assignment and outcome processes. The key contributions are to nonparametrically formalize the causal effect in a way that accounts for homophily, and to show how embedding methods can be used to identify and estimate this effect. Code is available at https://github.com/IrinaCristali/Peer-Contagion-on-Networks.
Adaptive Differentially Private Empirical Risk Minimization
Oct 25, 2021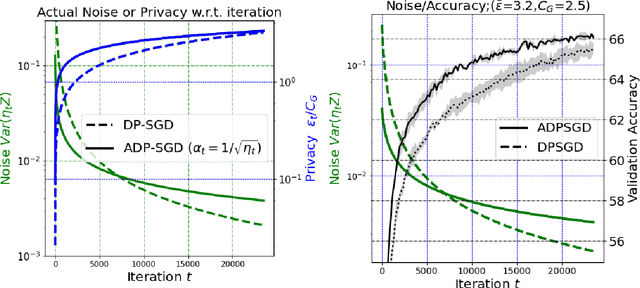
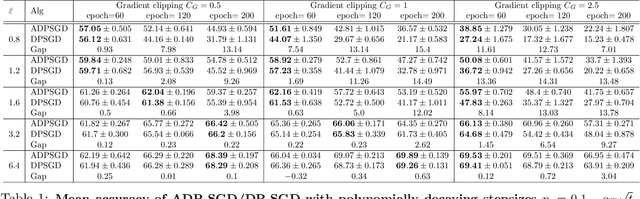
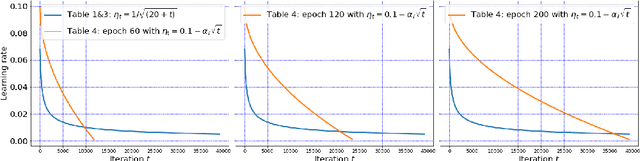
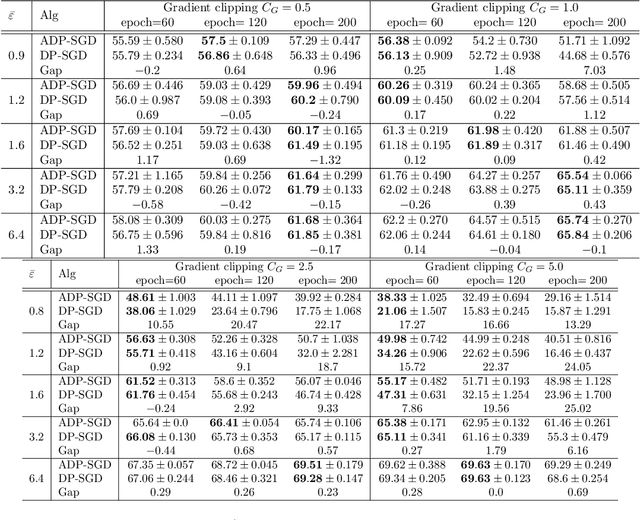
Abstract:We propose an adaptive (stochastic) gradient perturbation method for differentially private empirical risk minimization. At each iteration, the random noise added to the gradient is optimally adapted to the stepsize; we name this process adaptive differentially private (ADP) learning. Given the same privacy budget, we prove that the ADP method considerably improves the utility guarantee compared to the standard differentially private method in which vanilla random noise is added. Our method is particularly useful for gradient-based algorithms with time-varying learning rates, including variants of AdaGrad (Duchi et al., 2011). We provide extensive numerical experiments to demonstrate the effectiveness of the proposed adaptive differentially private algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge