An Asynchronous Decentralised Optimisation Algorithm for Nonconvex Problems

In this paper, we consider nonconvex decentralised optimisation and learning over a network of distributed agents. We develop an ADMM algorithm based on the Randomised Block Coordinate Douglas-Rachford splitting method which enables agents in the network to distributedly and asynchronously compute a set of first-order stationary solutions of the problem. To the best of our knowledge, this is the first decentralised and asynchronous algorithm for solving nonconvex optimisation problems with convergence proof. The numerical examples demonstrate the efficiency of the proposed algorithm for distributed Phase Retrieval and sparse Principal Component Analysis problems.

ZORMS-LfD: Learning from Demonstrations with Zeroth-Order Random Matrix Search

We propose Zeroth-Order Random Matrix Search for Learning from Demonstrations (ZORMS-LfD). ZORMS-LfD enables the costs, constraints, and dynamics of constrained optimal control problems, in both continuous and discrete time, to be learned from expert demonstrations without requiring smoothness of the learning-loss landscape. In contrast, existing state-of-the-art first-order methods require the existence and computation of gradients of the costs, constraints, dynamics, and learning loss with respect to states, controls and/or parameters. Most existing methods are also tailored to discrete time, with constrained problems in continuous time receiving only cursory attention. We demonstrate that ZORMS-LfD matches or surpasses the performance of state-of-the-art methods in terms of both learning loss and compute time across a variety of benchmark problems. On unconstrained continuous-time benchmark problems, ZORMS-LfD achieves similar loss performance to state-of-the-art first-order methods with an over $80$\% reduction in compute time. On constrained continuous-time benchmark problems where there is no specialized state-of-the-art method, ZORMS-LfD is shown to outperform the commonly used gradient-free Nelder-Mead optimization method.

Minimisation of Quasar-Convex Functions Using Random Zeroth-Order Oracles

This study explores the performance of a random Gaussian smoothing zeroth-order (ZO) scheme for minimising quasar-convex (QC) and strongly quasar-convex (SQC) functions in both unconstrained and constrained settings. For the unconstrained problem, we establish the ZO algorithm's convergence to a global minimum along with its complexity when applied to both QC and SQC functions. For the constrained problem, we introduce the new notion of proximal-quasar-convexity and prove analogous results to the unconstrained case. Specifically, we show the complexity bounds and the convergence of the algorithm to a neighbourhood of a global minimum whose size can be controlled under a variance reduction scheme. Theoretical findings are illustrated through investigating the performance of the algorithm applied to a range of problems in machine learning and optimisation. Specifically, we observe scenarios where the ZO method outperforms gradient descent. We provide a possible explanation for this phenomenon.

Interior Point Differential Dynamic Programming, Redux

We present IPDDP2, a structure-exploiting algorithm for solving discrete-time, finite horizon optimal control problems with nonlinear constraints. Inequality constraints are handled using a primal-dual interior point formulation and step acceptance for equality constraints follows a line-search filter approach. The iterates of the algorithm are derived under the Differential Dynamic Programming (DDP) framework. Our numerical experiments evaluate IPDDP2 on four robotic motion planning problems. IPDDP2 reliably converges to low optimality error and exhibits local quadratic and global convergence from remote starting points. Notably, we showcase the robustness of IPDDP2 by using it to solve a contact-implicit, joint limited acrobot swing-up problem involving complementarity constraints from a range of initial conditions. We provide a full implementation of IPDDP2 in the Julia programming language.

Min-Max Optimisation for Nonconvex-Nonconcave Functions Using a Random Zeroth-Order Extragradient Algorithm

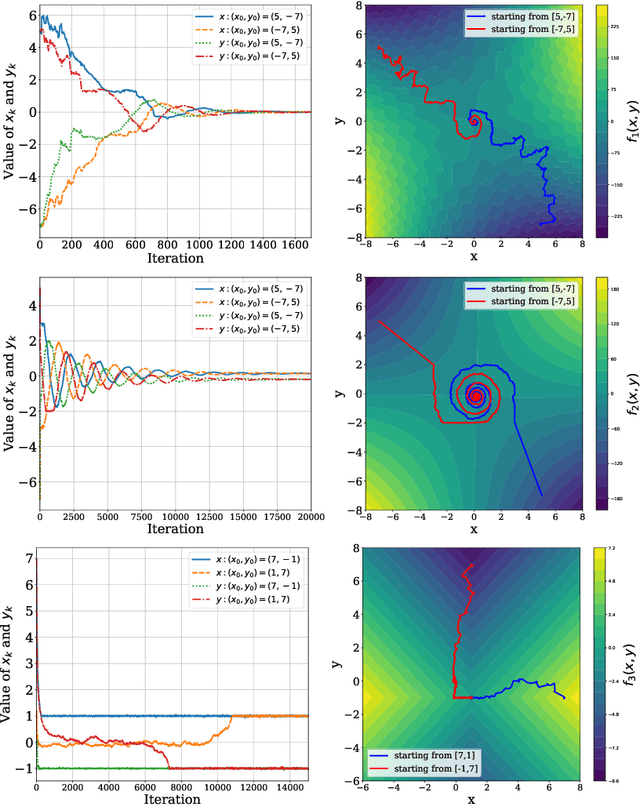
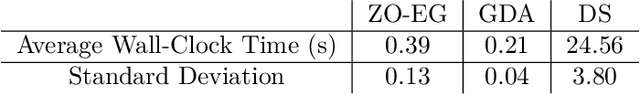
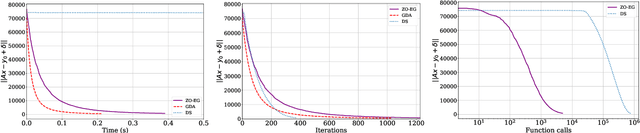
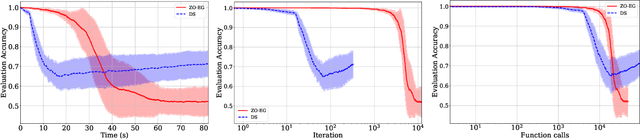
This study explores the performance of the random Gaussian smoothing Zeroth-Order ExtraGradient (ZO-EG) scheme considering min-max optimisation problems with possibly NonConvex-NonConcave (NC-NC) objective functions. We consider both unconstrained and constrained, differentiable and non-differentiable settings. We discuss the min-max problem from the point of view of variational inequalities. For the unconstrained problem, we establish the convergence of the ZO-EG algorithm to the neighbourhood of an $\epsilon$-stationary point of the NC-NC objective function, whose radius can be controlled under a variance reduction scheme, along with its complexity. For the constrained problem, we introduce the new notion of proximal variational inequalities and give examples of functions satisfying this property. Moreover, we prove analogous results to the unconstrained case for the constrained problem. For the non-differentiable case, we prove the convergence of the ZO-EG algorithm to a neighbourhood of an $\epsilon$-stationary point of the smoothed version of the objective function, where the radius of the neighbourhood can be controlled, which can be related to the ($\delta,\epsilon$)-Goldstein stationary point of the original objective function.

Properties of Fixed Points of Generalised Extra Gradient Methods Applied to Min-Max Problems

This paper studies properties of fixed points of generalised Extra-gradient (GEG) algorithms applied to min-max problems. We discuss connections between saddle points of the objective function of the min-max problem and GEG fixed points. We show that, under appropriate step-size selections, the set of saddle points (Nash equilibria) is a subset of stable fixed points of GEG. Convergence properties of the GEG algorithm are obtained through a stability analysis of a discrete-time dynamical system. The results and benefits when compared to existing methods are illustrated through numerical examples.

Joint State and Noise Covariance Estimation

This paper tackles the problem of jointly estimating the noise covariance matrix alongside primary parameters (such as poses and points) from measurements corrupted by Gaussian noise. In such settings, the noise covariance matrix determines the weights assigned to individual measurements in the least squares problem. We show that the joint problem exhibits a convex structure and provide a full characterization of the optimal noise covariance estimate (with analytical solutions) within joint maximum a posteriori and likelihood frameworks and several variants. Leveraging this theoretical result, we propose two novel algorithms that jointly estimate the primary parameters and the noise covariance matrix. To validate our approach, we conduct extensive experiments across diverse scenarios and offer practical insights into their application in robotics and computer vision estimation problems with a particular focus on SLAM.

A Behavior Tree-inspired programming language for autonomous agents

We propose a design for a functional programming language for autonomous agents, built off the ideas and motivations of Behavior Trees (BTs). BTs are a popular model for designing agents behavior in robotics and AI. However, as their growth has increased dramatically, the simple model of BTs has come to be limiting. There is a growing push to increase the functionality of BTs, with the end goal of BTs evolving into a programming language in their own right, centred around the defining BT properties of modularity and reactiveness. In this paper, we examine how the BT model must be extended in order to grow into such a language. We identify some fundamental problems which must be solved: implementing `reactive' selection, 'monitoring' safety-critical conditions, and passing data between actions. We provide a variety of small examples which demonstrate that these problems are complex, and that current BT approaches do not handle them in a manner consistent with modularity. We instead provide a simple set of modular programming primitives for handling these use cases, and show how they can be combined to build complex programs. We present a full specification for our BT-inspired language, and give an implementation in the functional programming language Haskell. Finally, we demonstrate our language by translating a large and complex BT into a simple, unambiguous program.

Improving Visual Place Recognition Based Robot Navigation Through Verification of Localization Estimates

Visual Place Recognition (VPR) systems often have imperfect performance, which affects robot navigation decisions. This research introduces a novel Multi-Layer Perceptron (MLP) integrity monitor for VPR which demonstrates improved performance and generalizability over the previous state-of-the-art SVM approach, removing per-environment training and reducing manual tuning requirements. We test our proposed system in extensive real-world experiments, where we also present two real-time integrity-based VPR verification methods: an instantaneous rejection method for a robot navigating to a goal zone (Experiment 1); and a historical method that takes a best, verified, match from its recent trajectory and uses an odometer to extrapolate forwards to a current position estimate (Experiment 2). Noteworthy results for Experiment 1 include a decrease in aggregate mean along-track goal error from ~9.8m to ~3.1m in missions the robot pursued to completion, and an increase in the aggregate rate of successful mission completion from ~41% to ~55%. Experiment 2 showed a decrease in aggregate mean along-track localization error from ~2.0m to ~0.5m, and an increase in the aggregate precision of localization attempts from ~97% to ~99%. Overall, our results demonstrate the practical usefulness of a VPR integrity monitor in real-world robotics to improve VPR localization and consequent navigation performance.

Online Non-Stationary Stochastic Quasar-Convex Optimization

Recent research has shown that quasar-convexity can be found in applications such as identification of linear dynamical systems and generalized linear models. Such observations have in turn spurred exciting developments in design and analysis algorithms that exploit quasar-convexity. In this work, we study the online stochastic quasar-convex optimization problems in a dynamic environment. We establish regret bounds of online gradient descent in terms of cumulative path variation and cumulative gradient variance for losses satisfying quasar-convexity and strong quasar-convexity. We then apply the results to generalized linear models (GLM) when the underlying parameter is time-varying. We establish regret bounds of online gradient descent when applying to GLMs with leaky ReLU activation function, logistic activation function, and ReLU activation function. Numerical results are presented to corroborate our findings.