Comment on "Blessings of Multiple Causes"

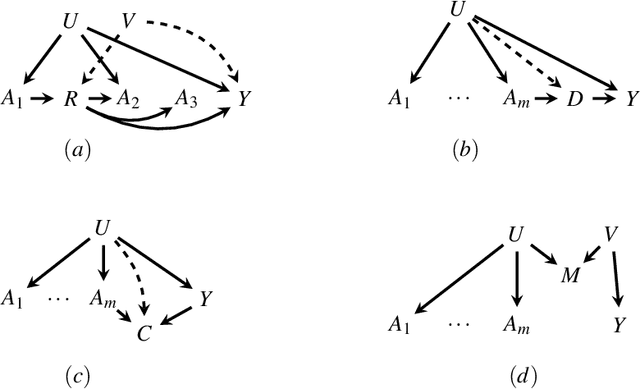
(This comment has been updated to respond to Wang and Blei's rejoinder [arXiv:1910.07320].) The premise of the deconfounder method proposed in "Blessings of Multiple Causes" by Wang and Blei [arXiv:1805.06826], namely that a variable that renders multiple causes conditionally independent also controls for unmeasured multi-cause confounding, is incorrect. This can be seen by noting that no fact about the observed data alone can be informative about ignorability, since ignorability is compatible with any observed data distribution. Methods to control for unmeasured confounding may be valid with additional assumptions in specific settings, but they cannot, in general, provide a checkable approach to causal inference, and they do not, in general, require weaker assumptions than the assumptions that are commonly used for causal inference. While this is outside the scope of this comment, we note that much recent work on applying ideas from latent variable modeling to causal inference problems suffers from similar issues.

Optimal Training of Fair Predictive Models

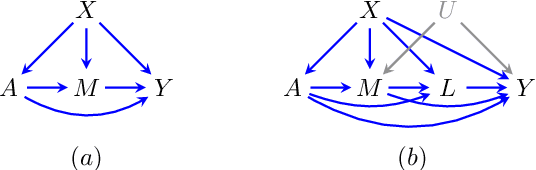
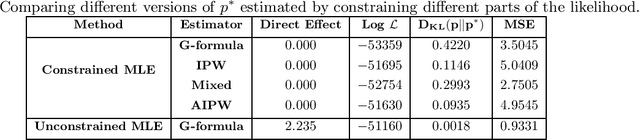
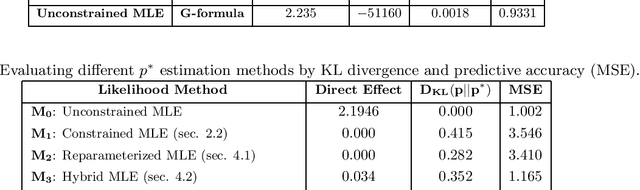
Recently there has been sustained interest in modifying prediction algorithms to satisfy fairness constraints. These constraints are typically complex nonlinear functionals of the observed data distribution. Focusing on the causal constraints proposed by Nabi and Shpitser (2018), we introduce new theoretical results and optimization techniques to make model training easier and more accurate. Specifically, we show how to reparameterize the observed data likelihood such that fairness constraints correspond directly to parameters that appear in the likelihood, transforming a complex constrained optimization objective into a simple optimization problem with box constraints. We also exploit methods from empirical likelihood theory in statistics to improve predictive performance, without requiring parametric models for high-dimensional feature vectors.

Identification In Missing Data Models Represented By Directed Acyclic Graphs

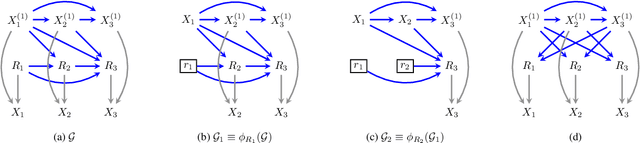
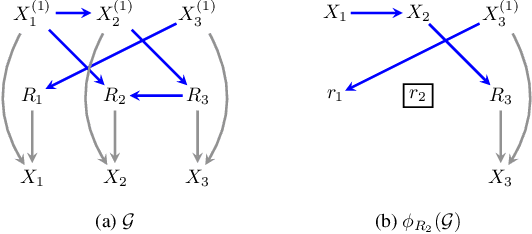
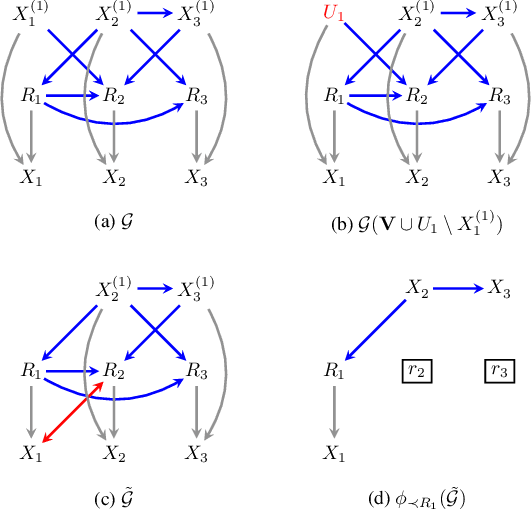
Missing data is a pervasive problem in data analyses, resulting in datasets that contain censored realizations of a target distribution. Many approaches to inference on the target distribution using censored observed data, rely on missing data models represented as a factorization with respect to a directed acyclic graph. In this paper we consider the identifiability of the target distribution within this class of models, and show that the most general identification strategies proposed so far retain a significant gap in that they fail to identify a wide class of identifiable distributions. To address this gap, we propose a new algorithm that significantly generalizes the types of manipulations used in the ID algorithm, developed in the context of causal inference, in order to obtain identification.

Causal Inference Under Interference And Network Uncertainty

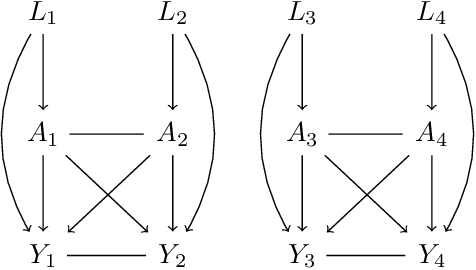
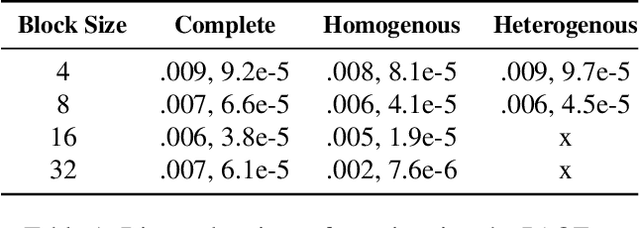
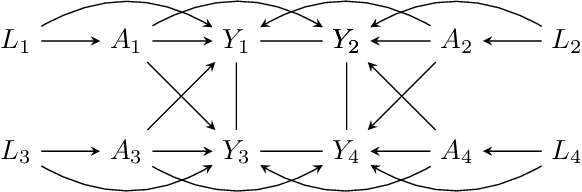
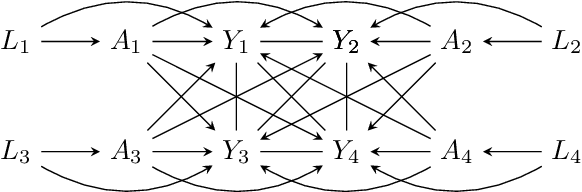
Classical causal and statistical inference methods typically assume the observed data consists of independent realizations. However, in many applications this assumption is inappropriate due to a network of dependences between units in the data. Methods for estimating causal effects have been developed in the setting where the structure of dependence between units is known exactly, but in practice there is often substantial uncertainty about the precise network structure. This is true, for example, in trial data drawn from vulnerable communities where social ties are difficult to query directly. In this paper we combine techniques from the structure learning and interference literatures in causal inference, proposing a general method for estimating causal effects under data dependence when the structure of this dependence is not known a priori. We demonstrate the utility of our method on synthetic datasets which exhibit network dependence.

Conditionally-additive-noise Models for Structure Learning

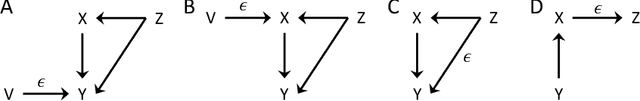
Constraint-based structure learning algorithms infer the causal structure of multivariate systems from observational data by determining an equivalent class of causal structures compatible with the conditional independencies in the data. Methods based on additive-noise (AN) models have been proposed to further discriminate between causal structures that are equivalent in terms of conditional independencies. These methods rely on a particular form of the generative functional equations, with an additive noise structure, which allows inferring the directionality of causation by testing the independence between the residuals of a nonlinear regression and the predictors (nrr-independencies). Full causal structure identifiability has been proven for systems that contain only additive-noise equations and have no hidden variables. We extend the AN framework in several ways. We introduce alternative regression-free tests of independence based on conditional variances (cv-independencies). We consider conditionally-additive-noise (CAN) models, in which the equations may have the AN form only after conditioning. We exploit asymmetries in nrr-independencies or cv-independencies resulting from the CAN form to derive a criterion that infers the causal relation between a pair of variables in a multivariate system without any assumption about the form of the equations or the presence of hidden variables.

Challenges of Using Text Classifiers for Causal Inference

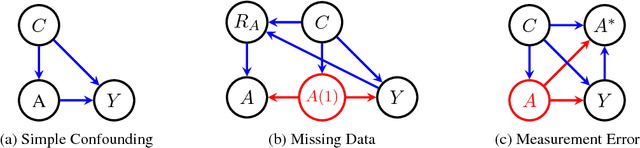
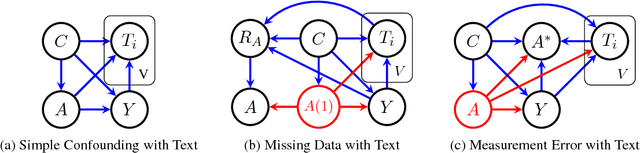
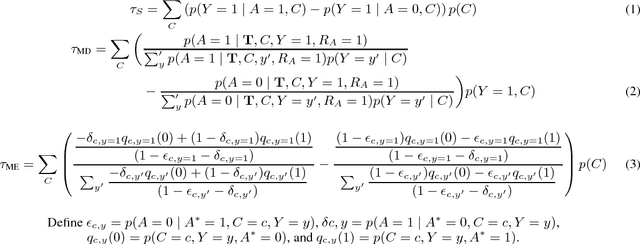
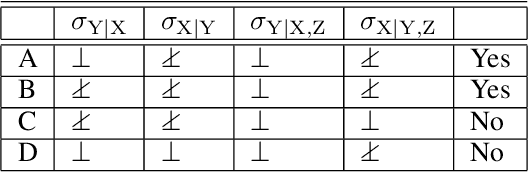
Causal understanding is essential for many kinds of decision-making, but causal inference from observational data has typically only been applied to structured, low-dimensional datasets. While text classifiers produce low-dimensional outputs, their use in causal inference has not previously been studied. To facilitate causal analyses based on language data, we consider the role that text classifiers can play in causal inference through established modeling mechanisms from the causality literature on missing data and measurement error. We demonstrate how to conduct causal analyses using text classifiers on simulated and Yelp data, and discuss the opportunities and challenges of future work that uses text data in causal inference.

Estimation of Personalized Effects Associated With Causal Pathways

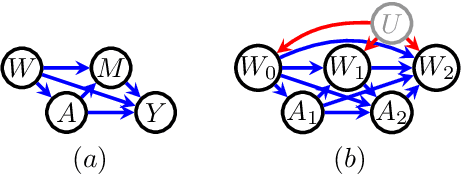
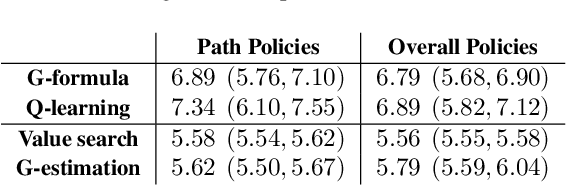
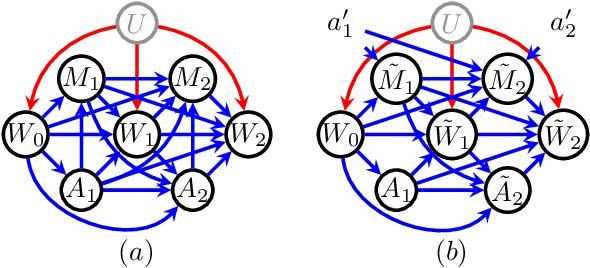
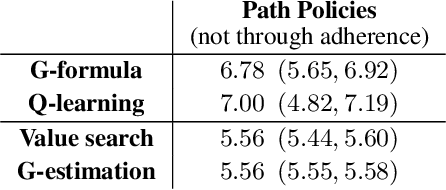
The goal of personalized decision making is to map a unit's characteristics to an action tailored to maximize the expected outcome for that unit. Obtaining high-quality mappings of this type is the goal of the dynamic regime literature. In healthcare settings, optimizing policies with respect to a particular causal pathway may be of interest as well. For example, we may wish to maximize the chemical effect of a drug given data from an observational study where the chemical effect of the drug on the outcome is entangled with the indirect effect mediated by differential adherence. In such cases, we may wish to optimize the direct effect of a drug, while keeping the indirect effect to that of some reference treatment. [16] shows how to combine mediation analysis and dynamic treatment regime ideas to defines policies associated with causal pathways and counterfactual responses to these policies. In this paper, we derive a variety of methods for learning high quality policies of this type from data, in a causal model corresponding to a longitudinal setting of practical importance. We illustrate our methods via a dataset of HIV patients undergoing therapy, gathered in the Nigerian PEPFAR program.

Learning Optimal Fair Policies

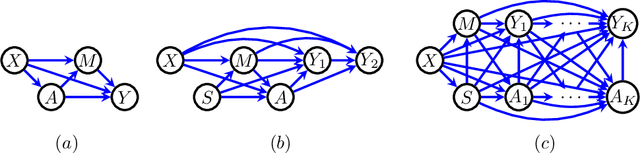
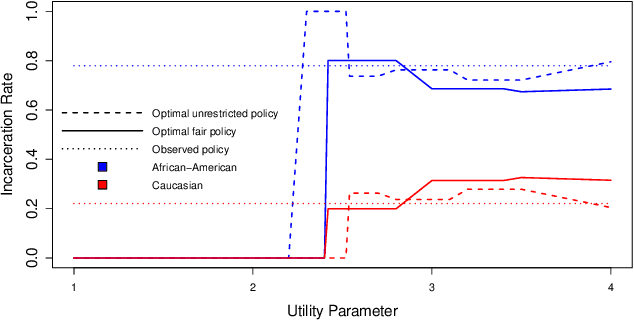
We consider the problem of learning optimal policies from observational data in a way that satisfies certain fairness criteria. The issue of fairness arises where some covariates used in decision making are sensitive features, or are correlated with sensitive features. (Nabi and Shpitser 2018) formalized fairness in the context of regression problems as constraining the causal effects of sensitive features along certain disallowed causal pathways. The existence of these causal effects may be called retrospective unfairness in the sense of already being present in the data before analysis begins, and may be due to discriminatory practices or the biased way in which variables are defined or recorded. In the context of learning policies, what we call prospective bias, i.e., the inappropriate dependence of learned policies on sensitive features, is also possible. In this paper, we use methods from causal and semiparametric inference to learn optimal policies in a way that addresses both retrospective bias in the data, and prospective bias due to the policy. In addition, our methods appropriately address statistical bias due to model misspecification and confounding bias, which are important in the estimation of path-specific causal effects from observational data. We apply our methods to both synthetic data and real criminal justice data.

Fair Inference On Outcomes

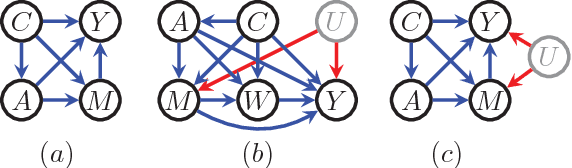
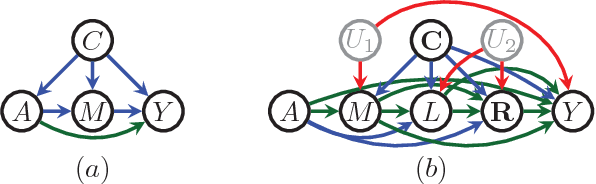
In this paper, we consider the problem of fair statistical inference involving outcome variables. Examples include classification and regression problems, and estimating treatment effects in randomized trials or observational data. The issue of fairness arises in such problems where some covariates or treatments are "sensitive," in the sense of having potential of creating discrimination. In this paper, we argue that the presence of discrimination can be formalized in a sensible way as the presence of an effect of a sensitive covariate on the outcome along certain causal pathways, a view which generalizes (Pearl, 2009). A fair outcome model can then be learned by solving a constrained optimization problem. We discuss a number of complications that arise in classical statistical inference due to this view and provide workarounds based on recent work in causal and semi-parametric inference.

Sparse Nested Markov models with Log-linear Parameters

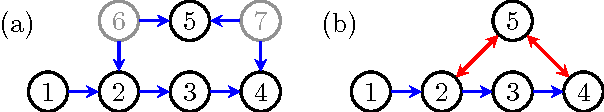
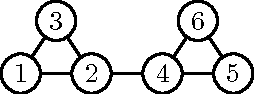
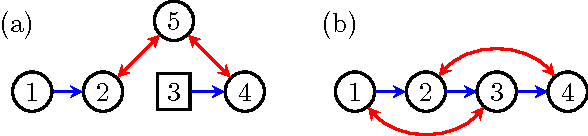
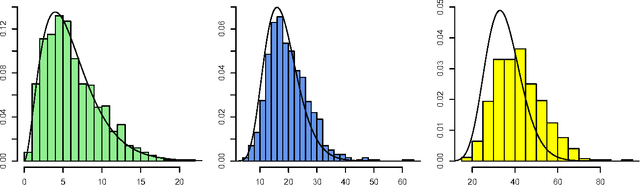
Hidden variables are ubiquitous in practical data analysis, and therefore modeling marginal densities and doing inference with the resulting models is an important problem in statistics, machine learning, and causal inference. Recently, a new type of graphical model, called the nested Markov model, was developed which captures equality constraints found in marginals of directed acyclic graph (DAG) models. Some of these constraints, such as the so called `Verma constraint', strictly generalize conditional independence. To make modeling and inference with nested Markov models practical, it is necessary to limit the number of parameters in the model, while still correctly capturing the constraints in the marginal of a DAG model. Placing such limits is similar in spirit to sparsity methods for undirected graphical models, and regression models. In this paper, we give a log-linear parameterization which allows sparse modeling with nested Markov models. We illustrate the advantages of this parameterization with a simulation study.