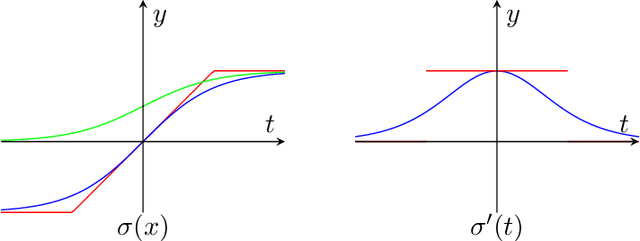
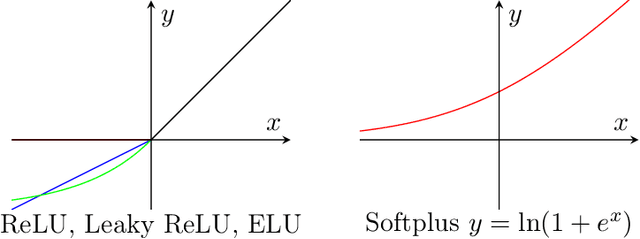
Learning a Single Neuron with Adversarial Label Noise via Gradient Descent

We study the fundamental problem of learning a single neuron, i.e., a function of the form $\mathbf{x}\mapsto\sigma(\mathbf{w}\cdot\mathbf{x})$ for monotone activations $\sigma:\mathbb{R}\mapsto\mathbb{R}$, with respect to the $L_2^2$-loss in the presence of adversarial label noise. Specifically, we are given labeled examples from a distribution $D$ on $(\mathbf{x}, y)\in\mathbb{R}^d \times \mathbb{R}$ such that there exists $\mathbf{w}^\ast\in\mathbb{R}^d$ achieving $F(\mathbf{w}^\ast)=\epsilon$, where $F(\mathbf{w})=\mathbf{E}_{(\mathbf{x},y)\sim D}[(\sigma(\mathbf{w}\cdot \mathbf{x})-y)^2]$. The goal of the learner is to output a hypothesis vector $\mathbf{w}$ such that $F(\mathbb{w})=C\, \epsilon$ with high probability, where $C>1$ is a universal constant. As our main contribution, we give efficient constant-factor approximate learners for a broad class of distributions (including log-concave distributions) and activation functions. Concretely, for the class of isotropic log-concave distributions, we obtain the following important corollaries: For the logistic activation, we obtain the first polynomial-time constant factor approximation (even under the Gaussian distribution). Our algorithm has sample complexity $\widetilde{O}(d/\epsilon)$, which is tight within polylogarithmic factors. For the ReLU activation, we give an efficient algorithm with sample complexity $\tilde{O}(d\, \polylog(1/\epsilon))$. Prior to our work, the best known constant-factor approximate learner had sample complexity $\tilde{\Omega}(d/\epsilon)$. In both of these settings, our algorithms are simple, performing gradient-descent on the (regularized) $L_2^2$-loss. The correctness of our algorithms relies on novel structural results that we establish, showing that (essentially all) stationary points of the underlying non-convex loss are approximately optimal.

List-Decodable Sparse Mean Estimation via Difference-of-Pairs Filtering

We study the problem of list-decodable sparse mean estimation. Specifically, for a parameter $\alpha \in (0, 1/2)$, we are given $m$ points in $\mathbb{R}^n$, $\lfloor \alpha m \rfloor$ of which are i.i.d. samples from a distribution $D$ with unknown $k$-sparse mean $\mu$. No assumptions are made on the remaining points, which form the majority of the dataset. The goal is to return a small list of candidates containing a vector $\widehat \mu$ such that $\| \widehat \mu - \mu \|_2$ is small. Prior work had studied the problem of list-decodable mean estimation in the dense setting. In this work, we develop a novel, conceptually simpler technique for list-decodable mean estimation. As the main application of our approach, we provide the first sample and computationally efficient algorithm for list-decodable sparse mean estimation. In particular, for distributions with ``certifiably bounded'' $t$-th moments in $k$-sparse directions and sufficiently light tails, our algorithm achieves error of $(1/\alpha)^{O(1/t)}$ with sample complexity $m = (k\log(n))^{O(t)}/\alpha$ and running time $\mathrm{poly}(mn^t)$. For the special case of Gaussian inliers, our algorithm achieves the optimal error guarantee of $\Theta (\sqrt{\log(1/\alpha)})$ with quasi-polynomial sample and computational complexity. We complement our upper bounds with nearly-matching statistical query and low-degree polynomial testing lower bounds.

Optimal SQ Lower Bounds for Robustly Learning Discrete Product Distributions and Ising Models

We establish optimal Statistical Query (SQ) lower bounds for robustly learning certain families of discrete high-dimensional distributions. In particular, we show that no efficient SQ algorithm with access to an $\epsilon$-corrupted binary product distribution can learn its mean within $\ell_2$-error $o(\epsilon \sqrt{\log(1/\epsilon)})$. Similarly, we show that no efficient SQ algorithm with access to an $\epsilon$-corrupted ferromagnetic high-temperature Ising model can learn the model to total variation distance $o(\epsilon \log(1/\epsilon))$. Our SQ lower bounds match the error guarantees of known algorithms for these problems, providing evidence that current upper bounds for these tasks are best possible. At the technical level, we develop a generic SQ lower bound for discrete high-dimensional distributions starting from low dimensional moment matching constructions that we believe will find other applications. Additionally, we introduce new ideas to analyze these moment-matching constructions for discrete univariate distributions.

Robust Sparse Mean Estimation via Sum of Squares

We study the problem of high-dimensional sparse mean estimation in the presence of an $\epsilon$-fraction of adversarial outliers. Prior work obtained sample and computationally efficient algorithms for this task for identity-covariance subgaussian distributions. In this work, we develop the first efficient algorithms for robust sparse mean estimation without a priori knowledge of the covariance. For distributions on $\mathbb R^d$ with "certifiably bounded" $t$-th moments and sufficiently light tails, our algorithm achieves error of $O(\epsilon^{1-1/t})$ with sample complexity $m = (k\log(d))^{O(t)}/\epsilon^{2-2/t}$. For the special case of the Gaussian distribution, our algorithm achieves near-optimal error of $\tilde O(\epsilon)$ with sample complexity $m = O(k^4 \mathrm{polylog}(d))/\epsilon^2$. Our algorithms follow the Sum-of-Squares based, proofs to algorithms approach. We complement our upper bounds with Statistical Query and low-degree polynomial testing lower bounds, providing evidence that the sample-time-error tradeoffs achieved by our algorithms are qualitatively the best possible.

Streaming Algorithms for High-Dimensional Robust Statistics

We study high-dimensional robust statistics tasks in the streaming model. A recent line of work obtained computationally efficient algorithms for a range of high-dimensional robust estimation tasks. Unfortunately, all previous algorithms require storing the entire dataset, incurring memory at least quadratic in the dimension. In this work, we develop the first efficient streaming algorithms for high-dimensional robust statistics with near-optimal memory requirements (up to logarithmic factors). Our main result is for the task of high-dimensional robust mean estimation in (a strengthening of) Huber's contamination model. We give an efficient single-pass streaming algorithm for this task with near-optimal error guarantees and space complexity nearly-linear in the dimension. As a corollary, we obtain streaming algorithms with near-optimal space complexity for several more complex tasks, including robust covariance estimation, robust regression, and more generally robust stochastic optimization.

Non-Gaussian Component Analysis via Lattice Basis Reduction

Non-Gaussian Component Analysis (NGCA) is the following distribution learning problem: Given i.i.d. samples from a distribution on $\mathbb{R}^d$ that is non-gaussian in a hidden direction $v$ and an independent standard Gaussian in the orthogonal directions, the goal is to approximate the hidden direction $v$. Prior work \cite{DKS17-sq} provided formal evidence for the existence of an information-computation tradeoff for NGCA under appropriate moment-matching conditions on the univariate non-gaussian distribution $A$. The latter result does not apply when the distribution $A$ is discrete. A natural question is whether information-computation tradeoffs persist in this setting. In this paper, we answer this question in the negative by obtaining a sample and computationally efficient algorithm for NGCA in the regime that $A$ is discrete or nearly discrete, in a well-defined technical sense. The key tool leveraged in our algorithm is the LLL method \cite{LLL82} for lattice basis reduction.

Outlier-Robust Sparse Estimation via Non-Convex Optimization

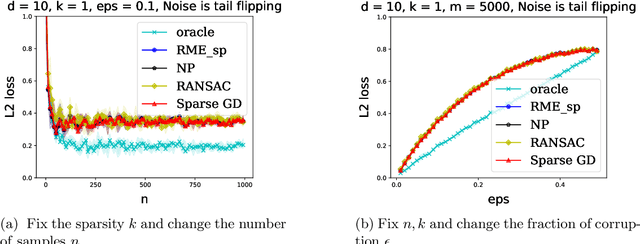
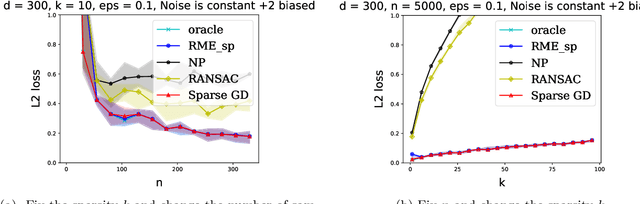
We explore the connection between outlier-robust high-dimensional statistics and non-convex optimization in the presence of sparsity constraints, with a focus on the fundamental tasks of robust sparse mean estimation and robust sparse PCA. We develop novel and simple optimization formulations for these problems such that any approximate stationary point of the associated optimization problem yields a near-optimal solution for the underlying robust estimation task. As a corollary, we obtain that any first-order method that efficiently converges to stationarity yields an efficient algorithm for these tasks. The obtained algorithms are simple, practical, and succeed under broader distributional assumptions compared to prior work.

ReLU Regression with Massart Noise

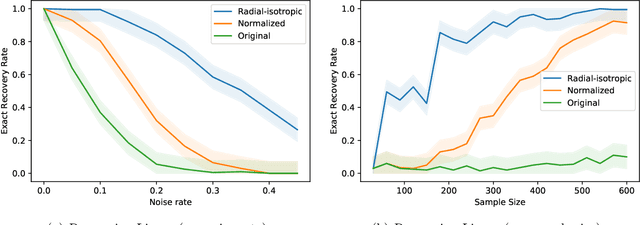
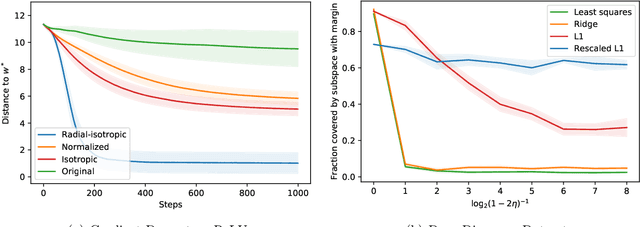
We study the fundamental problem of ReLU regression, where the goal is to fit Rectified Linear Units (ReLUs) to data. This supervised learning task is efficiently solvable in the realizable setting, but is known to be computationally hard with adversarial label noise. In this work, we focus on ReLU regression in the Massart noise model, a natural and well-studied semi-random noise model. In this model, the label of every point is generated according to a function in the class, but an adversary is allowed to change this value arbitrarily with some probability, which is {\em at most} $\eta < 1/2$. We develop an efficient algorithm that achieves exact parameter recovery in this model under mild anti-concentration assumptions on the underlying distribution. Such assumptions are necessary for exact recovery to be information-theoretically possible. We demonstrate that our algorithm significantly outperforms naive applications of $\ell_1$ and $\ell_2$ regression on both synthetic and real data.

Threshold Phenomena in Learning Halfspaces with Massart Noise

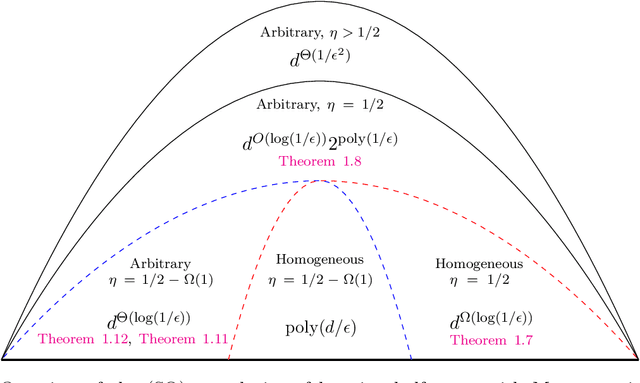
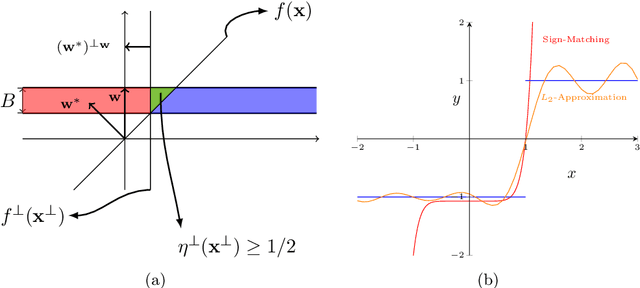
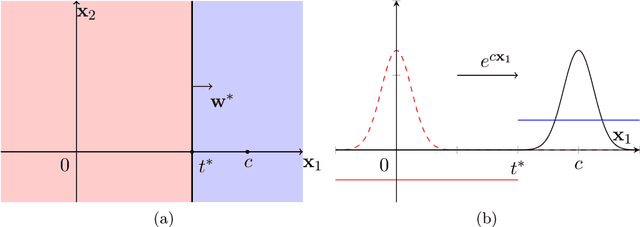
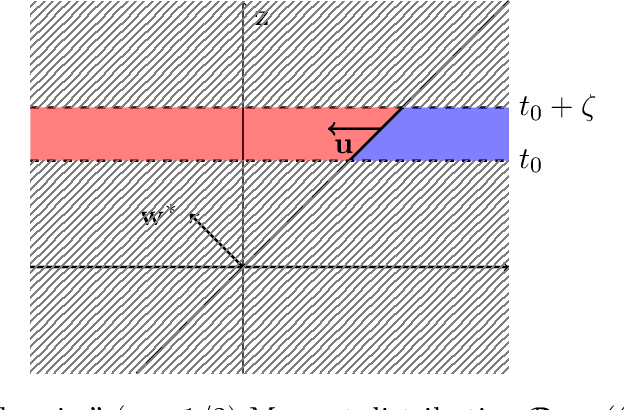
We study the problem of PAC learning halfspaces on $\mathbb{R}^d$ with Massart noise under Gaussian marginals. In the Massart noise model, an adversary is allowed to flip the label of each point $\mathbf{x}$ with probability $\eta(\mathbf{x}) \leq \eta$, for some parameter $\eta \in [0,1/2]$. The goal of the learner is to output a hypothesis with missclassification error $\mathrm{opt} + \epsilon$, where $\mathrm{opt}$ is the error of the target halfspace. Prior work studied this problem assuming that the target halfspace is homogeneous and that the parameter $\eta$ is strictly smaller than $1/2$. We explore how the complexity of the problem changes when either of these assumptions is removed, establishing the following threshold phenomena: For $\eta = 1/2$, we prove a lower bound of $d^{\Omega (\log(1/\epsilon))}$ on the complexity of any Statistical Query (SQ) algorithm for the problem, which holds even for homogeneous halfspaces. On the positive side, we give a new learning algorithm for arbitrary halfspaces in this regime with sample complexity and running time $O_\epsilon(1) \, d^{O(\log(1/\epsilon))}$. For $\eta <1/2$, we establish a lower bound of $d^{\Omega(\log(1/\gamma))}$ on the SQ complexity of the problem, where $\gamma = \max\{\epsilon, \min\{\mathbf{Pr}[f(\mathbf{x}) = 1], \mathbf{Pr}[f(\mathbf{x}) = -1]\} \}$ and $f$ is the target halfspace. In particular, this implies an SQ lower bound of $d^{\Omega (\log(1/\epsilon) )}$ for learning arbitrary Massart halfspaces (even for small constant $\eta$). We complement this lower bound with a new learning algorithm for this regime with sample complexity and runtime $d^{O_{\eta}(\log(1/\gamma))} \mathrm{poly}(1/\epsilon)$. Taken together, our results qualitatively characterize the complexity of learning halfspaces in the Massart model.

Forster Decomposition and Learning Halfspaces with Noise

A Forster transform is an operation that turns a distribution into one with good anti-concentration properties. While a Forster transform does not always exist, we show that any distribution can be efficiently decomposed as a disjoint mixture of few distributions for which a Forster transform exists and can be computed efficiently. As the main application of this result, we obtain the first polynomial-time algorithm for distribution-independent PAC learning of halfspaces in the Massart noise model with strongly polynomial sample complexity, i.e., independent of the bit complexity of the examples. Previous algorithms for this learning problem incurred sample complexity scaling polynomially with the bit complexity, even though such a dependence is not information-theoretically necessary.