Knowledge-based Transfer Learning Explanation

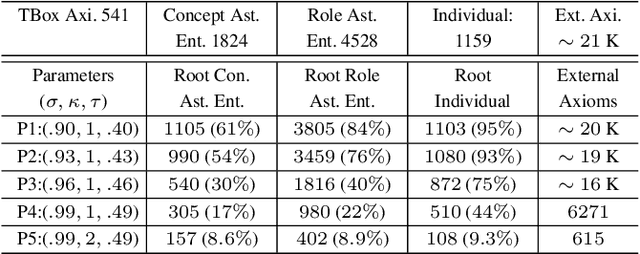
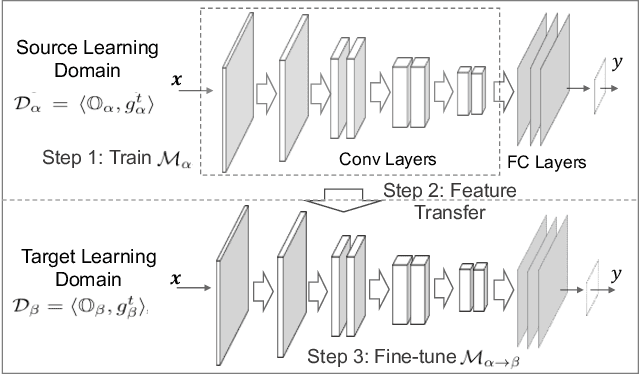
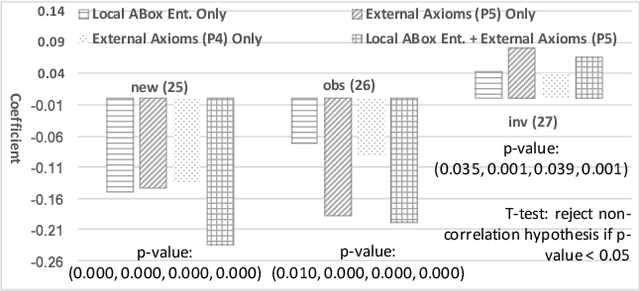
Machine learning explanation can significantly boost machine learning's application in decision making, but the usability of current methods is limited in human-centric explanation, especially for transfer learning, an important machine learning branch that aims at utilizing knowledge from one learning domain (i.e., a pair of dataset and prediction task) to enhance prediction model training in another learning domain. In this paper, we propose an ontology-based approach for human-centric explanation of transfer learning. Three kinds of knowledge-based explanatory evidence, with different granularities, including general factors, particular narrators and core contexts are first proposed and then inferred with both local ontologies and external knowledge bases. The evaluation with US flight data and DBpedia has presented their confidence and availability in explaining the transferability of feature representation in flight departure delay forecasting.

Consequence-based Reasoning for Description Logics with Disjunction, Inverse Roles, Number Restrictions, and Nominals

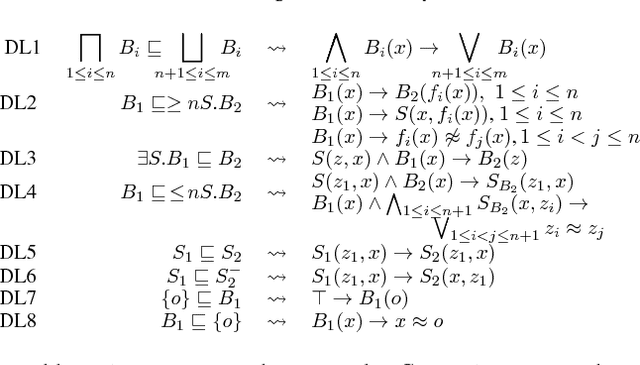
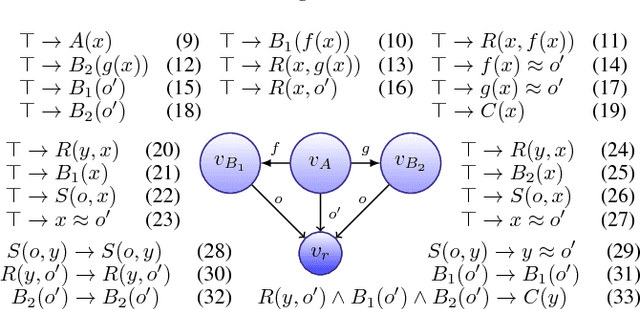
We present a consequence-based calculus for concept subsumption and classification in the description logic ALCHOIQ, which extends ALC with role hierarchies, inverse roles, number restrictions, and nominals. By using standard transformations, our calculus extends to SROIQ, which covers all of OWL 2 DL except for datatypes. A key feature of our calculus is its pay-as-you-go behaviour: unlike existing algorithms, our calculus is worst-case optimal for all the well-known proper fragments of ALCHOIQ, albeit not for the full logic.

Stratified Negation in Limit Datalog Programs

There has recently been an increasing interest in declarative data analysis, where analytic tasks are specified using a logical language, and their implementation and optimisation are delegated to a general-purpose query engine. Existing declarative languages for data analysis can be formalised as variants of logic programming equipped with arithmetic function symbols and/or aggregation, and are typically undecidable. In prior work, the language of $\mathit{limit\ programs}$ was proposed, which is sufficiently powerful to capture many analysis tasks and has decidable entailment problem. Rules in this language, however, do not allow for negation. In this paper, we study an extension of limit programs with stratified negation-as-failure. We show that the additional expressive power makes reasoning computationally more demanding, and provide tight data complexity bounds. We also identify a fragment with tractable data complexity and sufficient expressivity to capture many relevant tasks.

Optimised Maintenance of Datalog Materialisations

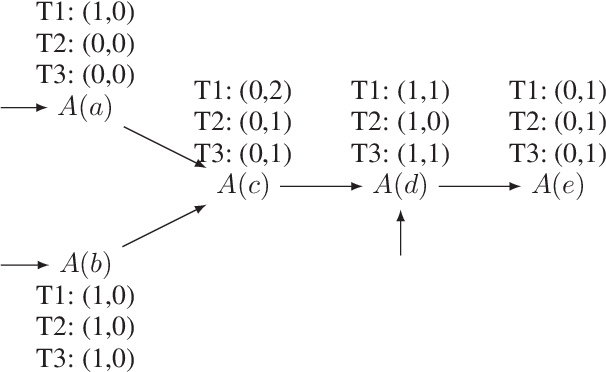
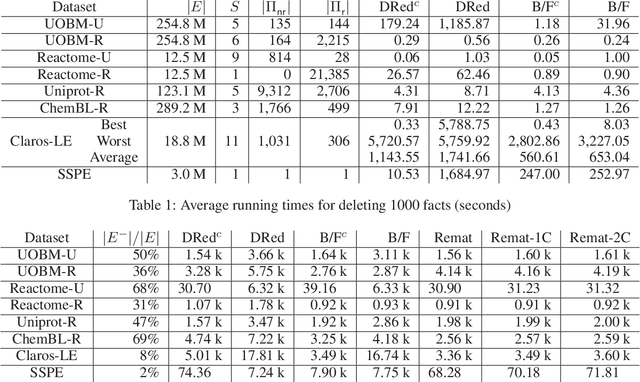
To efficiently answer queries, datalog systems often materialise all consequences of a datalog program, so the materialisation must be updated whenever the input facts change. Several solutions to the materialisation update problem have been proposed. The Delete/Rederive (DRed) and the Backward/Forward (B/F) algorithms solve this problem for general datalog, but both contain steps that evaluate rules 'backwards' by matching their heads to a fact and evaluating the partially instantiated rule bodies as queries. We show that this can be a considerable source of overhead even on very small updates. In contrast, the Counting algorithm does not evaluate the rules 'backwards', but it can handle only nonrecursive rules. We present two hybrid approaches that combine DRed and B/F with Counting so as to reduce or even eliminate 'backward' rule evaluation while still handling arbitrary datalog programs. We show empirically that our hybrid algorithms are usually significantly faster than existing approaches, sometimes by orders of magnitude.

Foundations of Declarative Data Analysis Using Limit Datalog Programs

Motivated by applications in declarative data analysis, we study $\mathit{Datalog}_{\mathbb{Z}}$---an extension of positive Datalog with arithmetic functions over integers. This language is known to be undecidable, so we propose two fragments. In $\mathit{limit}~\mathit{Datalog}_{\mathbb{Z}}$ predicates are axiomatised to keep minimal/maximal numeric values, allowing us to show that fact entailment is coNExpTime-complete in combined, and coNP-complete in data complexity. Moreover, an additional $\mathit{stability}$ requirement causes the complexity to drop to ExpTime and PTime, respectively. Finally, we show that stable $\mathit{Datalog}_{\mathbb{Z}}$ can express many useful data analysis tasks, and so our results provide a sound foundation for the development of advanced information systems.

Stream Reasoning in Temporal Datalog

In recent years, there has been an increasing interest in extending traditional stream processing engines with logical, rule-based, reasoning capabilities. This poses significant theoretical and practical challenges since rules can derive new information and propagate it both towards past and future time points; as a result, streamed query answers can depend on data that has not yet been received, as well as on data that arrived far in the past. Stream reasoning algorithms, however, must be able to stream out query answers as soon as possible, and can only keep a limited number of previous input facts in memory. In this paper, we propose novel reasoning problems to deal with these challenges, and study their computational properties on Datalog extended with a temporal sort and the successor function (a core rule-based language for stream reasoning applications).

The Bag Semantics of Ontology-Based Data Access

Ontology-based data access (OBDA) is a popular approach for integrating and querying multiple data sources by means of a shared ontology. The ontology is linked to the sources using mappings, which assign views over the data to ontology predicates. Motivated by the need for OBDA systems supporting database-style aggregate queries, we propose a bag semantics for OBDA, where duplicate tuples in the views defined by the mappings are retained, as is the case in standard databases. We show that bag semantics makes conjunctive query answering in OBDA coNP-hard in data complexity. To regain tractability, we consider a rather general class of queries and show its rewritability to a generalisation of the relational calculus to bags.

Towards Analytics Aware Ontology Based Access to Static and Streaming Data (Extended Version)

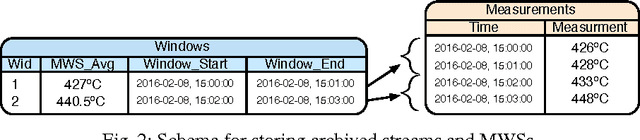
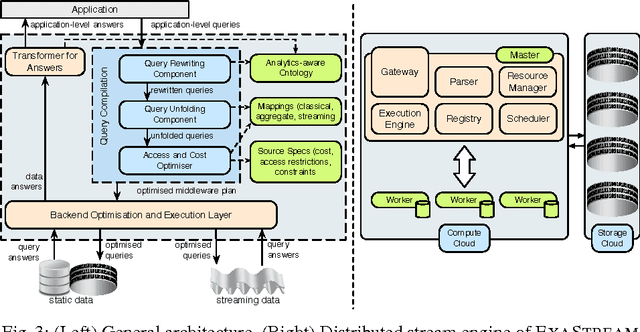
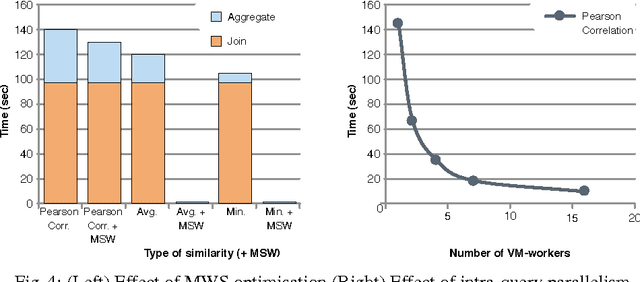
Real-time analytics that requires integration and aggregation of heterogeneous and distributed streaming and static data is a typical task in many industrial scenarios such as diagnostics of turbines in Siemens. OBDA approach has a great potential to facilitate such tasks; however, it has a number of limitations in dealing with analytics that restrict its use in important industrial applications. Based on our experience with Siemens, we argue that in order to overcome those limitations OBDA should be extended and become analytics, source, and cost aware. In this work we propose such an extension. In particular, we propose an ontology, mapping, and query language for OBDA, where aggregate and other analytical functions are first class citizens. Moreover, we develop query optimisation techniques that allow to efficiently process analytical tasks over static and streaming data. We implement our approach in a system and evaluate our system with Siemens turbine data.

Extending Consequence-Based Reasoning to SRIQ

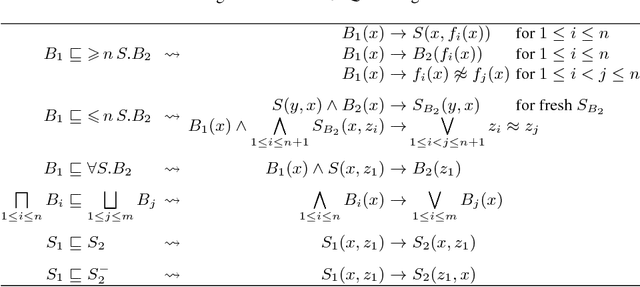
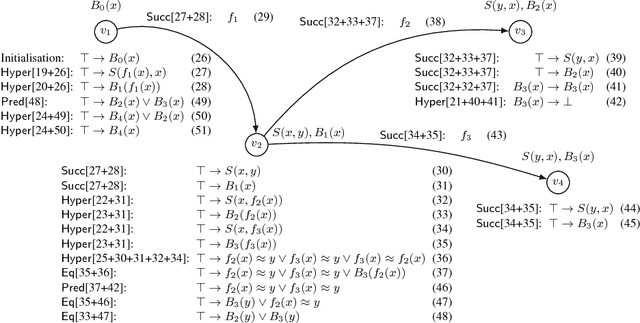
Consequence-based calculi are a family of reasoning algorithms for description logics (DLs), and they combine hypertableau and resolution in a way that often achieves excellent performance in practice. Up to now, however, they were proposed for either Horn DLs (which do not support disjunction), or for DLs without counting quantifiers. In this paper we present a novel consequence-based calculus for SRIQ---a rich DL that supports both features. This extension is non-trivial since the intermediate consequences that need to be derived during reasoning cannot be captured using DLs themselves. The results of our preliminary performance evaluation suggest the feasibility of our approach in practice.

Ontology Module Extraction via Datalog Reasoning

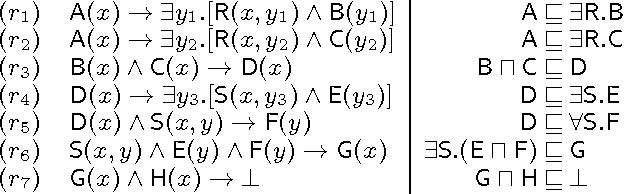
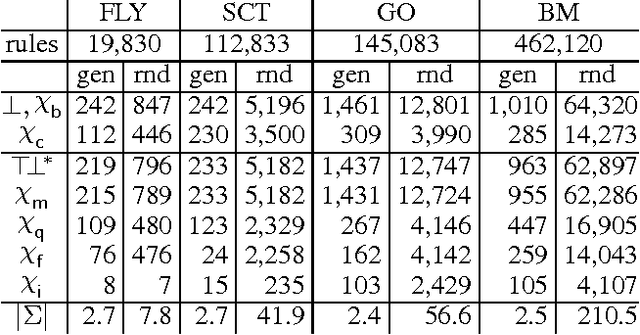
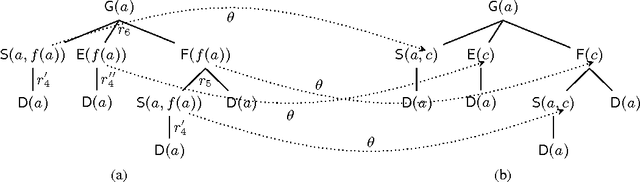
Module extraction - the task of computing a (preferably small) fragment M of an ontology T that preserves entailments over a signature S - has found many applications in recent years. Extracting modules of minimal size is, however, computationally hard, and often algorithmically infeasible. Thus, practical techniques are based on approximations, where M provably captures the relevant entailments, but is not guaranteed to be minimal. Existing approximations, however, ensure that M preserves all second-order entailments of T w.r.t. S, which is stronger than is required in many applications, and may lead to large modules in practice. In this paper we propose a novel approach in which module extraction is reduced to a reasoning problem in datalog. Our approach not only generalises existing approximations in an elegant way, but it can also be tailored to preserve only specific kinds of entailments, which allows us to extract significantly smaller modules. An evaluation on widely-used ontologies has shown very encouraging results.