XLinear: A Lightweight and Accurate MLP-Based Model for Long-Term Time Series Forecasting with Exogenous Inputs

Despite the prevalent assumption of uniform variable importance in long-term time series forecasting models, real world applications often exhibit asymmetric causal relationships and varying data acquisition costs. Specifically, cost-effective exogenous data (e.g., local weather) can unilaterally influence dynamics of endogenous variables, such as lake surface temperature. Exploiting these links enables more effective forecasts when exogenous inputs are readily available. Transformer-based models capture long-range dependencies but incur high computation and suffer from permutation invariance. Patch-based variants improve efficiency yet can miss local temporal patterns. To efficiently exploit informative signals across both the temporal dimension and relevant exogenous variables, this study proposes XLinear, a lightweight time series forecasting model built upon MultiLayer Perceptrons (MLPs). XLinear uses a global token derived from an endogenous variable as a pivotal hub for interacting with exogenous variables, and employs MLPs with sigmoid activation to extract both temporal patterns and variate-wise dependencies. Its prediction head then integrates these signals to forecast the endogenous series. We evaluate XLinear on seven standard benchmarks and five real-world datasets with exogenous inputs. Compared with state-of-the-art models, XLinear delivers superior accuracy and efficiency for both multivariate forecasts and univariate forecasts influenced by exogenous inputs.

A New Local Distance-Based Outlier Detection Approach for Scattered Real-World Data

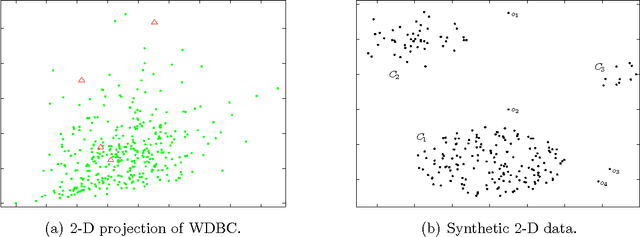
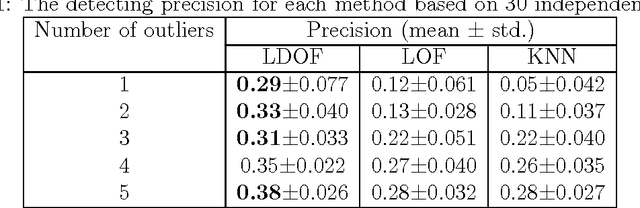
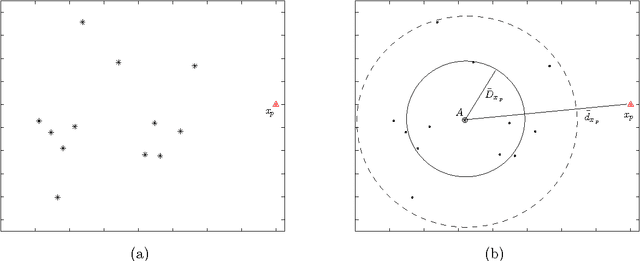
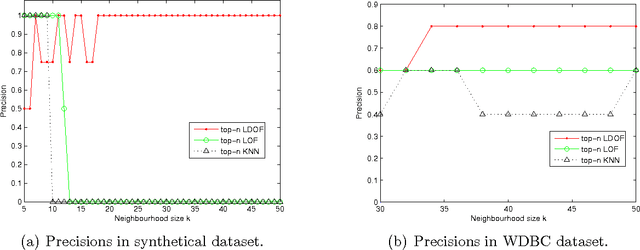
Detecting outliers which are grossly different from or inconsistent with the remaining dataset is a major challenge in real-world KDD applications. Existing outlier detection methods are ineffective on scattered real-world datasets due to implicit data patterns and parameter setting issues. We define a novel "Local Distance-based Outlier Factor" (LDOF) to measure the {outlier-ness} of objects in scattered datasets which addresses these issues. LDOF uses the relative location of an object to its neighbours to determine the degree to which the object deviates from its neighbourhood. Properties of LDOF are theoretically analysed including LDOF's lower bound and its false-detection probability, as well as parameter settings. In order to facilitate parameter settings in real-world applications, we employ a top-n technique in our outlier detection approach, where only the objects with the highest LDOF values are regarded as outliers. Compared to conventional approaches (such as top-n KNN and top-n LOF), our method top-n LDOF is more effective at detecting outliers in scattered data. It is also easier to set parameters, since its performance is relatively stable over a large range of parameter values, as illustrated by experimental results on both real-world and synthetic datasets.