In-Context Algorithm Emulation in Fixed-Weight Transformers

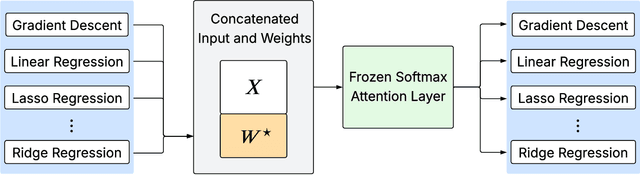
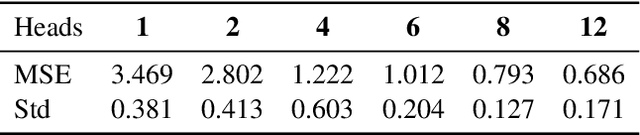
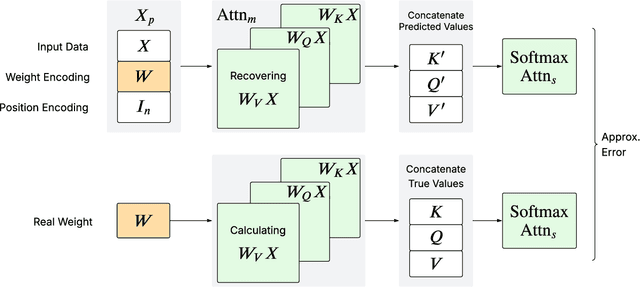
We prove that a minimal Transformer architecture with frozen weights is capable of emulating a broad class of algorithms by in-context prompting. In particular, for any algorithm implementable by a fixed-weight attention head (e.g. one-step gradient descent or linear/ridge regression), there exists a prompt that drives a two-layer softmax attention module to reproduce the algorithm's output with arbitrary precision. This guarantee extends even to a single-head attention layer (using longer prompts if necessary), achieving architectural minimality. Our key idea is to construct prompts that encode an algorithm's parameters into token representations, creating sharp dot-product gaps that force the softmax attention to follow the intended computation. This construction requires no feed-forward layers and no parameter updates. All adaptation happens through the prompt alone. These findings forge a direct link between in-context learning and algorithmic emulation, and offer a simple mechanism for large Transformers to serve as prompt-programmable libraries of algorithms. They illuminate how GPT-style foundation models may swap algorithms via prompts alone, establishing a form of algorithmic universality in modern Transformer models.

Attention Mechanism, Max-Affine Partition, and Universal Approximation

We establish the universal approximation capability of single-layer, single-head self- and cross-attention mechanisms with minimal attached structures. Our key insight is to interpret single-head attention as an input domain-partition mechanism that assigns distinct values to subregions. This allows us to engineer the attention weights such that this assignment imitates the target function. Building on this, we prove that a single self-attention layer, preceded by sum-of-linear transformations, is capable of approximating any continuous function on a compact domain under the $L_\infty$-norm. Furthermore, we extend this construction to approximate any Lebesgue integrable function under $L_p$-norm for $1\leq p <\infty$. Lastly, we also extend our techniques and show that, for the first time, single-head cross-attention achieves the same universal approximation guarantees.

Universal Approximation with Softmax Attention

We prove that with linear transformations, both (i) two-layer self-attention and (ii) one-layer self-attention followed by a softmax function are universal approximators for continuous sequence-to-sequence functions on compact domains. Our main technique is a new interpolation-based method for analyzing attention's internal mechanism. This leads to our key insight: self-attention is able to approximate a generalized version of ReLU to arbitrary precision, and hence subsumes many known universal approximators. Building on these, we show that two-layer multi-head attention alone suffices as a sequence-to-sequence universal approximator. In contrast, prior works rely on feed-forward networks to establish universal approximation in Transformers. Furthermore, we extend our techniques to show that, (softmax-)attention-only layers are capable of approximating various statistical models in-context. We believe these techniques hold independent interest.