Recent advances in deep learning and language models for studying the microbiome

Recent advancements in deep learning, particularly large language models (LLMs), made a significant impact on how researchers study microbiome and metagenomics data. Microbial protein and genomic sequences, like natural languages, form a language of life, enabling the adoption of LLMs to extract useful insights from complex microbial ecologies. In this paper, we review applications of deep learning and language models in analyzing microbiome and metagenomics data. We focus on problem formulations, necessary datasets, and the integration of language modeling techniques. We provide an extensive overview of protein/genomic language modeling and their contributions to microbiome studies. We also discuss applications such as novel viromics language modeling, biosynthetic gene cluster prediction, and knowledge integration for metagenomics studies.

Wasserstein F-tests for Fréchet regression on Bures-Wasserstein manifolds

This paper considers the problem of regression analysis with random covariance matrix as outcome and Euclidean covariates in the framework of Fr\'echet regression on the Bures-Wasserstein manifold. Such regression problems have many applications in single cell genomics and neuroscience, where we have covariance matrix measured over a large set of samples. Fr\'echet regression on the Bures-Wasserstein manifold is formulated as estimating the conditional Fr\'echet mean given covariates $x$. A non-asymptotic $\sqrt{n}$-rate of convergence (up to $\log n$ factors) is obtained for our estimator $\hat{Q}_n(x)$ uniformly for $\left\|x\right\| \lesssim \sqrt{\log n}$, which is crucial for deriving the asymptotic null distribution and power of our proposed statistical test for the null hypothesis of no association. In addition, a central limit theorem for the point estimate $\hat{Q}_n(x)$ is obtained, giving insights to a test for covariate effects. The null distribution of the test statistic is shown to converge to a weighted sum of independent chi-squares, which implies that the proposed test has the desired significance level asymptotically. Also, the power performance of the test is demonstrated against a sequence of contiguous alternatives. Simulation results show the accuracy of the asymptotic distributions. The proposed methods are applied to a single cell gene expression data set that shows the change of gene co-expression network as people age.

Transfer Learning with Random Coefficient Ridge Regression

Ridge regression with random coefficients provides an important alternative to fixed coefficients regression in high dimensional setting when the effects are expected to be small but not zeros. This paper considers estimation and prediction of random coefficient ridge regression in the setting of transfer learning, where in addition to observations from the target model, source samples from different but possibly related regression models are available. The informativeness of the source model to the target model can be quantified by the correlation between the regression coefficients. This paper proposes two estimators of regression coefficients of the target model as the weighted sum of the ridge estimates of both target and source models, where the weights can be determined by minimizing the empirical estimation risk or prediction risk. Using random matrix theory, the limiting values of the optimal weights are derived under the setting when $p/n \rightarrow \gamma$, where $p$ is the number of the predictors and $n$ is the sample size, which leads to an explicit expression of the estimation or prediction risks. Simulations show that these limiting risks agree very well with the empirical risks. An application to predicting the polygenic risk scores for lipid traits shows such transfer learning methods lead to smaller prediction errors than the single sample ridge regression or Lasso-based transfer learning.

Transfer Learning for Contextual Multi-armed Bandits

Motivated by a range of applications, we study in this paper the problem of transfer learning for nonparametric contextual multi-armed bandits under the covariate shift model, where we have data collected on source bandits before the start of the target bandit learning. The minimax rate of convergence for the cumulative regret is established and a novel transfer learning algorithm that attains the minimax regret is proposed. The results quantify the contribution of the data from the source domains for learning in the target domain in the context of nonparametric contextual multi-armed bandits. In view of the general impossibility of adaptation to unknown smoothness, we develop a data-driven algorithm that achieves near-optimal statistical guarantees (up to a logarithmic factor) while automatically adapting to the unknown parameters over a large collection of parameter spaces under an additional self-similarity assumption. A simulation study is carried out to illustrate the benefits of utilizing the data from the auxiliary source domains for learning in the target domain.

Semi-Supervised Statistical Inference for High-Dimensional Linear Regression with Blockwise Missing Data

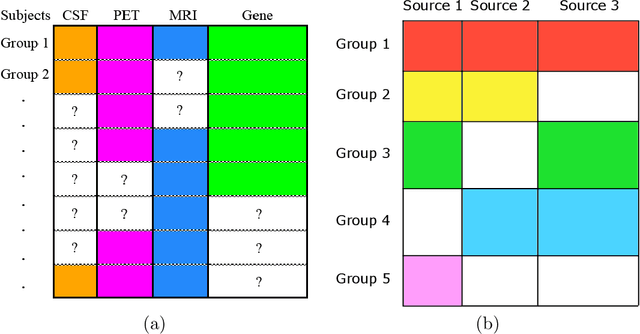
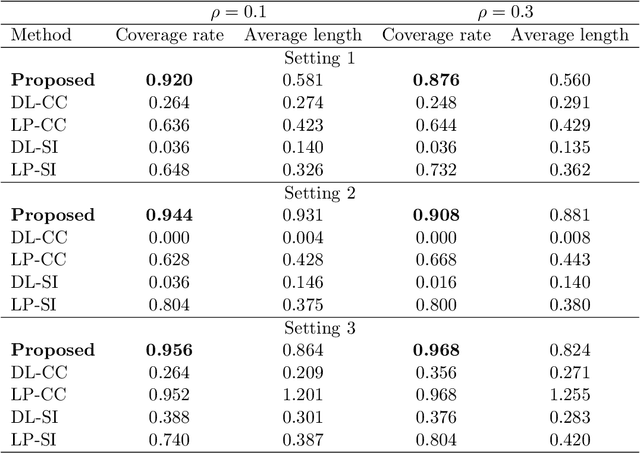
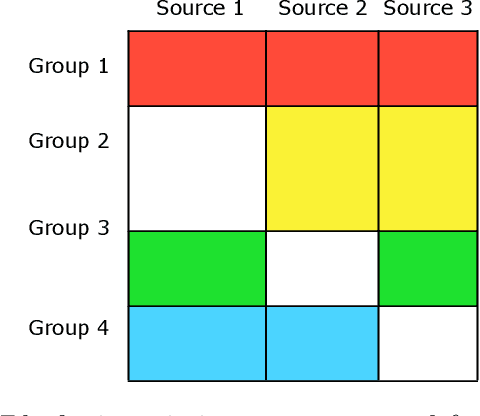
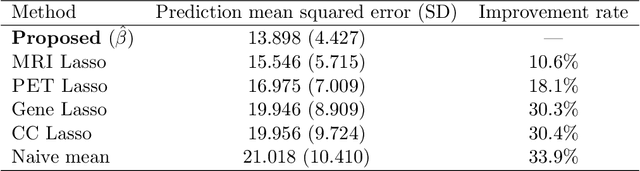
Blockwise missing data occurs frequently when we integrate multisource or multimodality data where different sources or modalities contain complementary information. In this paper, we consider a high-dimensional linear regression model with blockwise missing covariates and a partially observed response variable. Under this semi-supervised framework, we propose a computationally efficient estimator for the regression coefficient vector based on carefully constructed unbiased estimating equations and a multiple blockwise imputation procedure, and obtain its rates of convergence. Furthermore, building upon an innovative semi-supervised projected estimating equation technique that intrinsically achieves bias-correction of the initial estimator, we propose nearly unbiased estimators for the individual regression coefficients that are asymptotically normally distributed under mild conditions. By carefully analyzing these debiased estimators, asymptotically valid confidence intervals and statistical tests about each regression coefficient are constructed. Numerical studies and application analysis of the Alzheimer's Disease Neuroimaging Initiative data show that the proposed method performs better and benefits more from unsupervised samples than existing methods.

Estimation, Confidence Intervals, and Large-Scale Hypotheses Testing for High-Dimensional Mixed Linear Regression

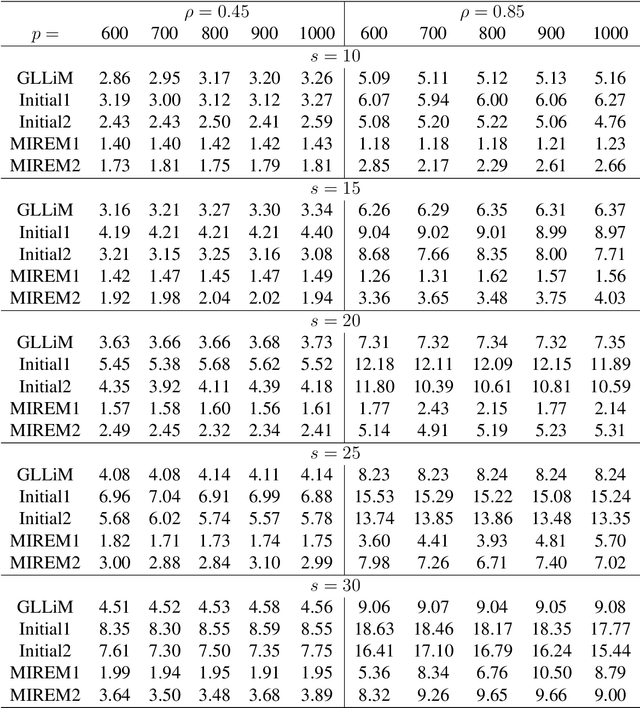
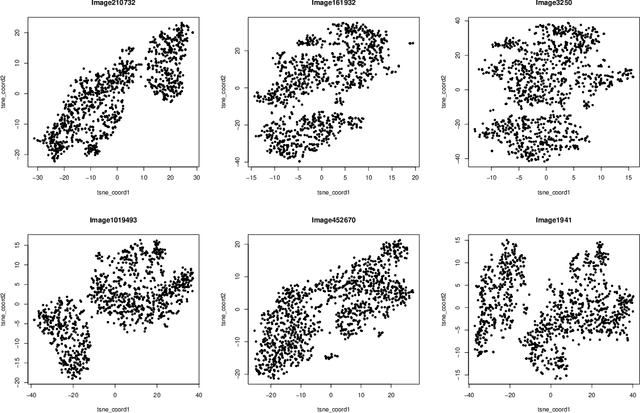
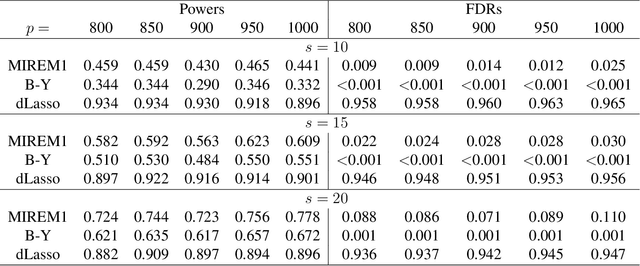
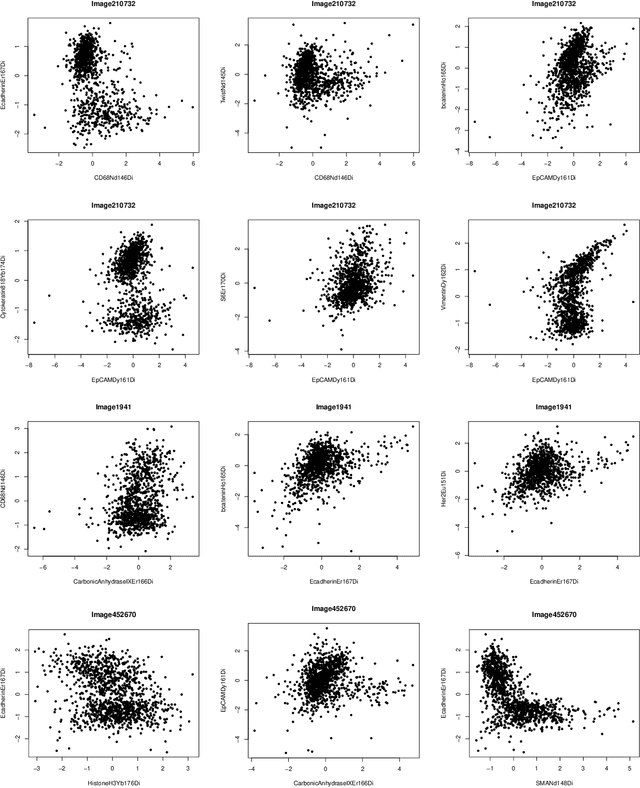
This paper studies the high-dimensional mixed linear regression (MLR) where the output variable comes from one of the two linear regression models with an unknown mixing proportion and an unknown covariance structure of the random covariates. Building upon a high-dimensional EM algorithm, we propose an iterative procedure for estimating the two regression vectors and establish their rates of convergence. Based on the iterative estimators, we further construct debiased estimators and establish their asymptotic normality. For individual coordinates, confidence intervals centered at the debiased estimators are constructed. Furthermore, a large-scale multiple testing procedure is proposed for testing the regression coefficients and is shown to control the false discovery rate (FDR) asymptotically. Simulation studies are carried out to examine the numerical performance of the proposed methods and their superiority over existing methods. The proposed methods are further illustrated through an analysis of a dataset of multiplex image cytometry, which investigates the interaction networks among the cellular phenotypes that include the expression levels of 20 epitopes or combinations of markers.

Transfer Learning in Large-scale Gaussian Graphical Models with False Discovery Rate Control

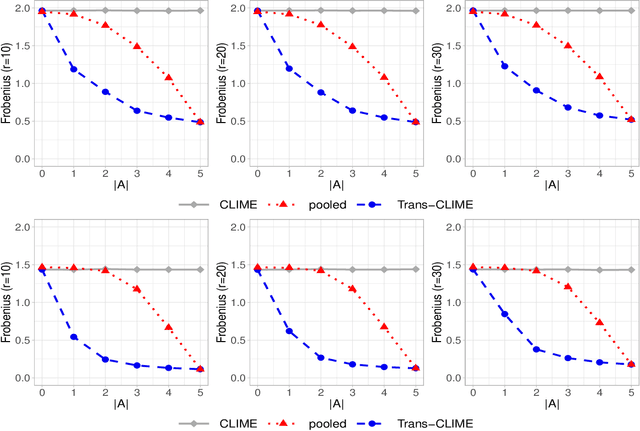
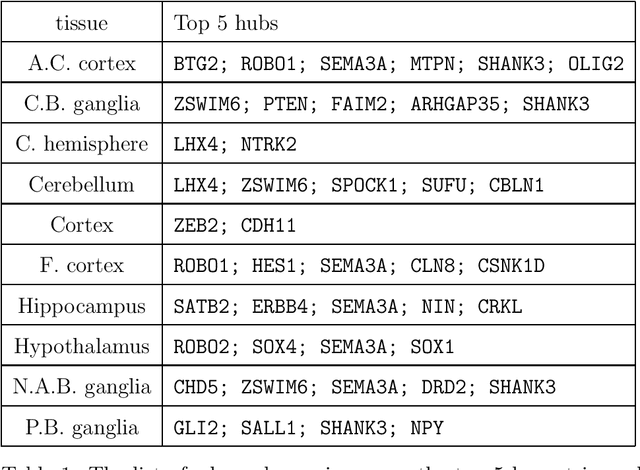
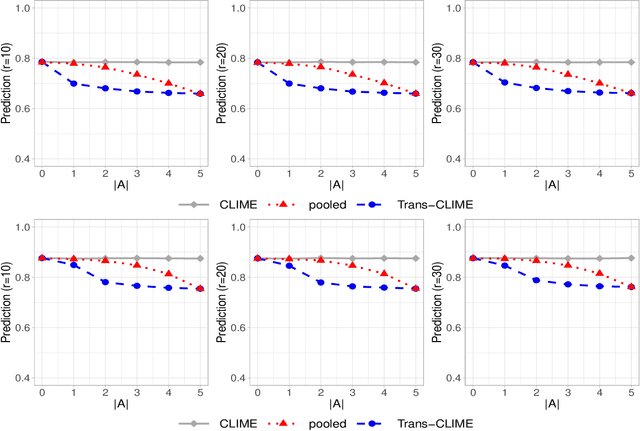
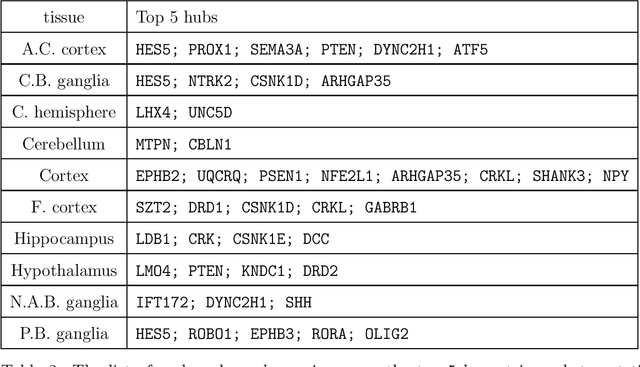
Transfer learning for high-dimensional Gaussian graphical models (GGMs) is studied with the goal of estimating the target GGM by utilizing the data from similar and related auxiliary studies. The similarity between the target graph and each auxiliary graph is characterized by the sparsity of a divergence matrix. An estimation algorithm, Trans-CLIME, is proposed and shown to attain a faster convergence rate than the minimax rate in the single study setting. Furthermore, a debiased Trans-CLIME estimator is introduced and shown to be element-wise asymptotically normal. It is used to construct a multiple testing procedure for edge detection with false discovery rate control. The proposed estimation and multiple testing procedures demonstrate superior numerical performance in simulations and are applied to infer the gene networks in a target brain tissue by leveraging the gene expressions from multiple other brain tissues. A significant decrease in prediction errors and a significant increase in power for link detection are observed.

Transfer Learning for High-dimensional Linear Regression: Prediction, Estimation, and Minimax Optimality

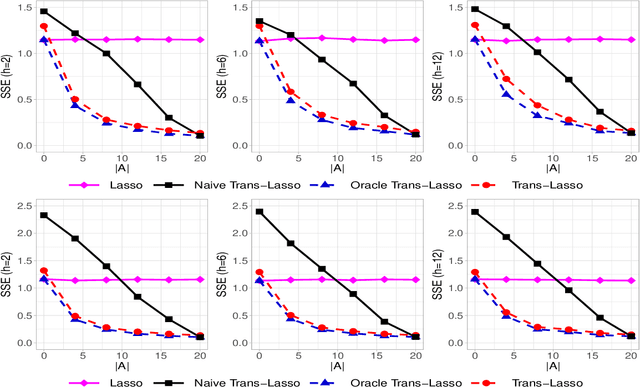
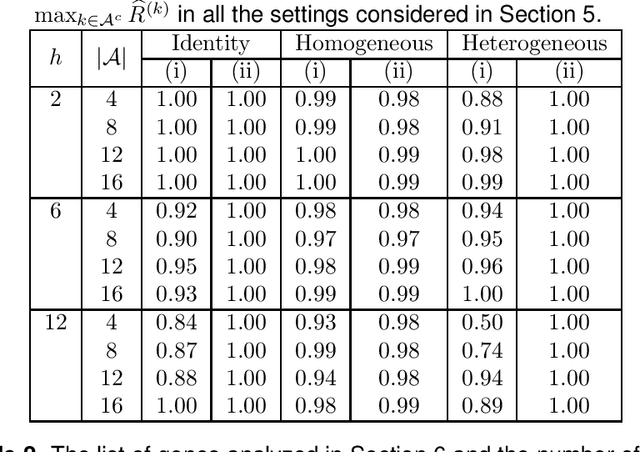
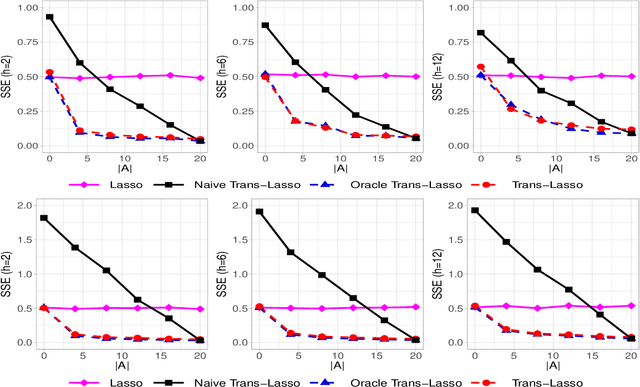
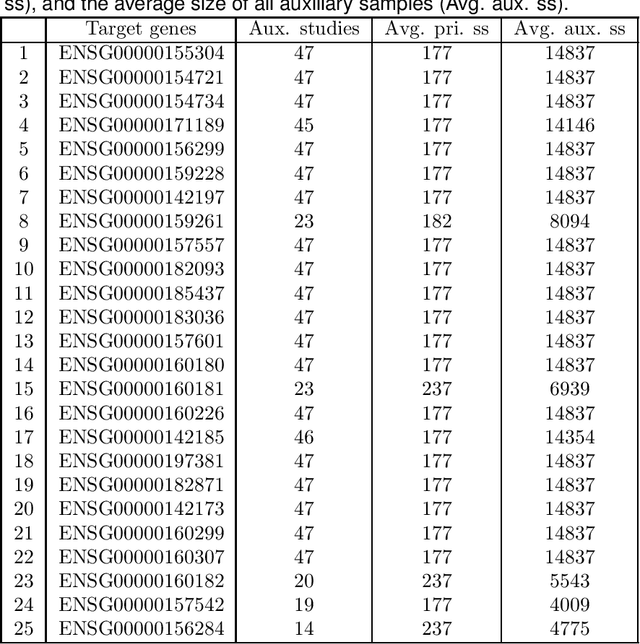
This paper considers the estimation and prediction of a high-dimensional linear regression in the setting of transfer learning, using samples from the target model as well as auxiliary samples from different but possibly related regression models. When the set of "informative" auxiliary samples is known, an estimator and a predictor are proposed and their optimality is established. The optimal rates of convergence for prediction and estimation are faster than the corresponding rates without using the auxiliary samples. This implies that knowledge from the informative auxiliary samples can be transferred to improve the learning performance of the target problem. In the case that the set of informative auxiliary samples is unknown, we propose a data-driven procedure for transfer learning, called Trans-Lasso, and reveal its robustness to non-informative auxiliary samples and its efficiency in knowledge transfer. The proposed procedures are demonstrated in numerical studies and are applied to a dataset concerning the associations among gene expressions. It is shown that Trans-Lasso leads to improved performance in gene expression prediction in a target tissue by incorporating the data from multiple different tissues as auxiliary samples.

Optimal Structured Principal Subspace Estimation: Metric Entropy and Minimax Rates

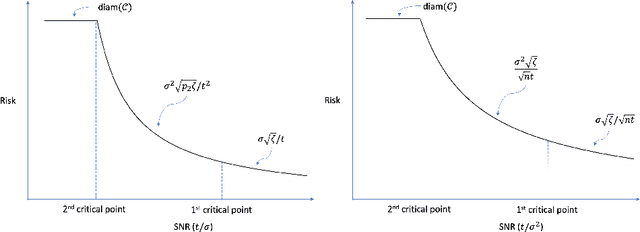
Driven by a wide range of applications, many principal subspace estimation problems have been studied individually under different structural constraints. This paper presents a unified framework for the statistical analysis of a general structured principal subspace estimation problem which includes as special cases non-negative PCA/SVD, sparse PCA/SVD, subspace constrained PCA/SVD, and spectral clustering. General minimax lower and upper bounds are established to characterize the interplay between the information-geometric complexity of the structural set for the principal subspaces, the signal-to-noise ratio (SNR), and the dimensionality. The results yield interesting phase transition phenomena concerning the rates of convergence as a function of the SNRs and the fundamental limit for consistent estimation. Applying the general results to the specific settings yields the minimax rates of convergence for those problems, including the previous unknown optimal rates for non-negative PCA/SVD, sparse SVD and subspace constrained PCA/SVD.

High Dimensional M-Estimation with Missing Outcomes: A Semi-Parametric Framework

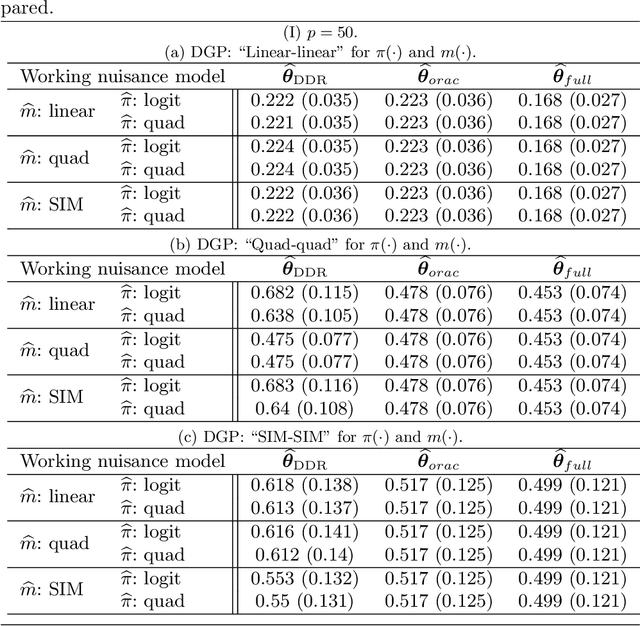
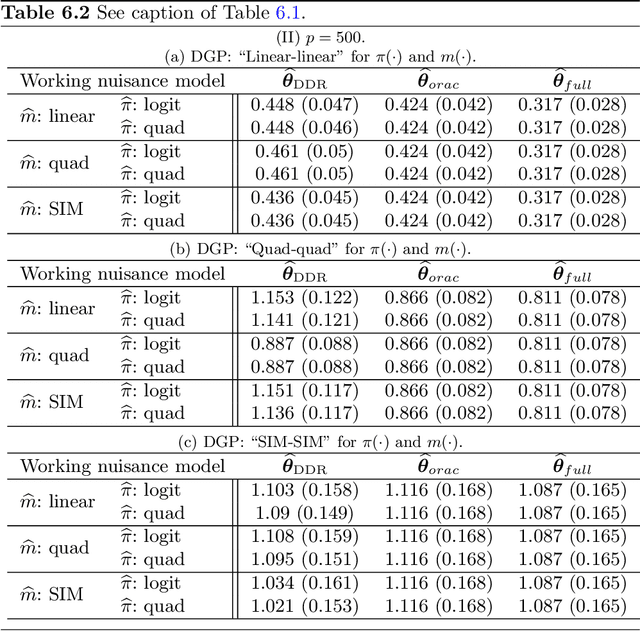
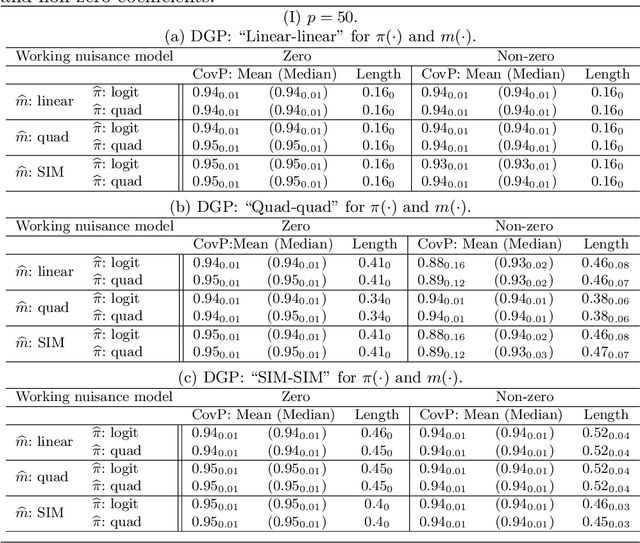
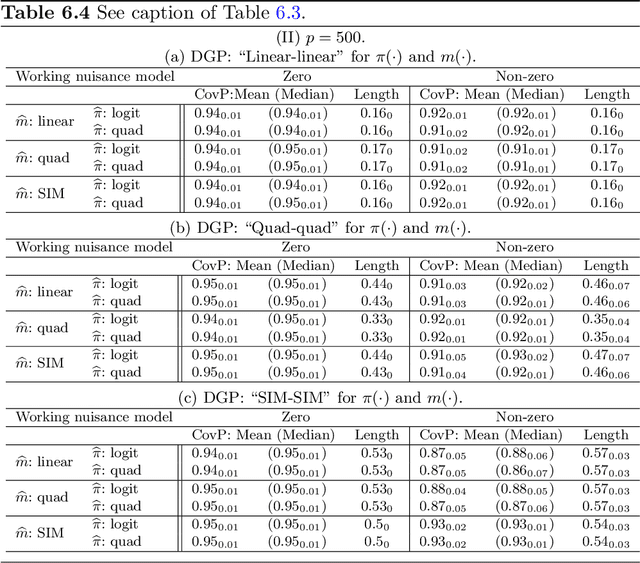
We consider high dimensional $M$-estimation in settings where the response $Y$ is possibly missing at random and the covariates $\mathbf{X} \in \mathbb{R}^p$ can be high dimensional compared to the sample size $n$. The parameter of interest $\boldsymbol{\theta}_0 \in \mathbb{R}^d$ is defined as the minimizer of the risk of a convex loss, under a fully non-parametric model, and $\boldsymbol{\theta}_0$ itself is high dimensional which is a key distinction from existing works. Standard high dimensional regression and series estimation with possibly misspecified models and missing $Y$ are included as special cases, as well as their counterparts in causal inference using 'potential outcomes'. Assuming $\boldsymbol{\theta}_0$ is $s$-sparse ($s \ll n$), we propose an $L_1$-regularized debiased and doubly robust (DDR) estimator of $\boldsymbol{\theta}_0$ based on a high dimensional adaptation of the traditional double robust (DR) estimator's construction. Under mild tail assumptions and arbitrarily chosen (working) models for the propensity score (PS) and the outcome regression (OR) estimators, satisfying only some high-level conditions, we establish finite sample performance bounds for the DDR estimator showing its (optimal) $L_2$ error rate to be $\sqrt{s (\log d)/ n}$ when both models are correct, and its consistency and DR properties when only one of them is correct. Further, when both the models are correct, we propose a desparsified version of our DDR estimator that satisfies an asymptotic linear expansion and facilitates inference on low dimensional components of $\boldsymbol{\theta}_0$. Finally, we discuss various of choices of high dimensional parametric/semi-parametric working models for the PS and OR estimators. All results are validated via detailed simulations.