Transfer Learning for Nonparametric Regression: Non-asymptotic Minimax Analysis and Adaptive Procedure

Transfer learning for nonparametric regression is considered. We first study the non-asymptotic minimax risk for this problem and develop a novel estimator called the confidence thresholding estimator, which is shown to achieve the minimax optimal risk up to a logarithmic factor. Our results demonstrate two unique phenomena in transfer learning: auto-smoothing and super-acceleration, which differentiate it from nonparametric regression in a traditional setting. We then propose a data-driven algorithm that adaptively achieves the minimax risk up to a logarithmic factor across a wide range of parameter spaces. Simulation studies are conducted to evaluate the numerical performance of the adaptive transfer learning algorithm, and a real-world example is provided to demonstrate the benefits of the proposed method.

The Expressive Power of Neural Networks: A View from the Width

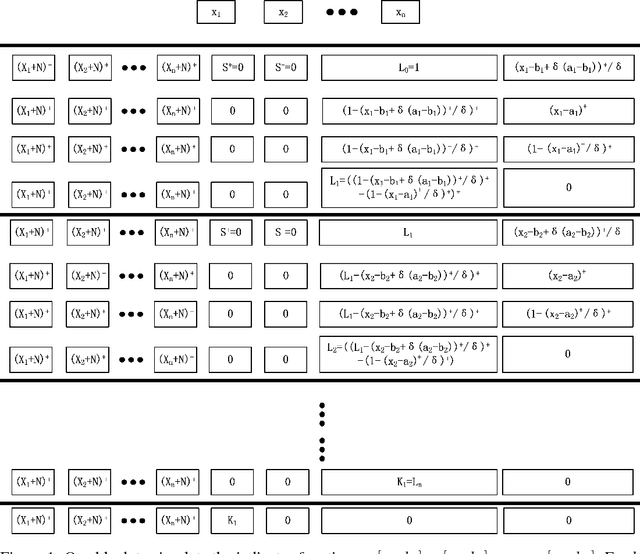
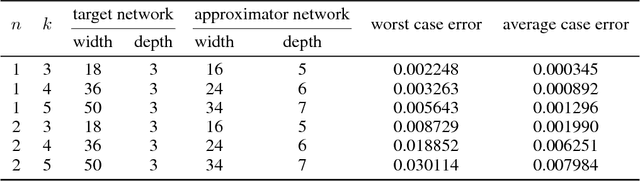
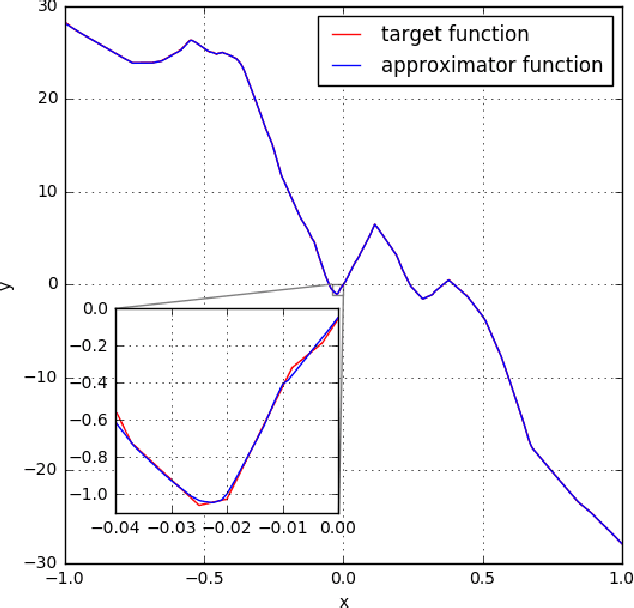
The expressive power of neural networks is important for understanding deep learning. Most existing works consider this problem from the view of the depth of a network. In this paper, we study how width affects the expressiveness of neural networks. Classical results state that depth-bounded (e.g. depth-$2$) networks with suitable activation functions are universal approximators. We show a universal approximation theorem for width-bounded ReLU networks: width-$(n+4)$ ReLU networks, where $n$ is the input dimension, are universal approximators. Moreover, except for a measure zero set, all functions cannot be approximated by width-$n$ ReLU networks, which exhibits a phase transition. Several recent works demonstrate the benefits of depth by proving the depth-efficiency of neural networks. That is, there are classes of deep networks which cannot be realized by any shallow network whose size is no more than an exponential bound. Here we pose the dual question on the width-efficiency of ReLU networks: Are there wide networks that cannot be realized by narrow networks whose size is not substantially larger? We show that there exist classes of wide networks which cannot be realized by any narrow network whose depth is no more than a polynomial bound. On the other hand, we demonstrate by extensive experiments that narrow networks whose size exceed the polynomial bound by a constant factor can approximate wide and shallow network with high accuracy. Our results provide more comprehensive evidence that depth is more effective than width for the expressiveness of ReLU networks.