Rate-matching the regret lower-bound in the linear quadratic regulator with unknown dynamics

The theory of reinforcement learning currently suffers from a mismatch between its empirical performance and the theoretical characterization of its performance, with consequences for, e.g., the understanding of sample efficiency, safety, and robustness. The linear quadratic regulator with unknown dynamics is a fundamental reinforcement learning setting with significant structure in its dynamics and cost function, yet even in this setting there is a gap between the best known regret lower-bound of $\Omega_p(\sqrt{T})$ and the best known upper-bound of $O_p(\sqrt{T}\,\text{polylog}(T))$. The contribution of this paper is to close that gap by establishing a novel regret upper-bound of $O_p(\sqrt{T})$. Our proof is constructive in that it analyzes the regret of a concrete algorithm, and simultaneously establishes an estimation error bound on the dynamics of $O_p(T^{-1/4})$ which is also the first to match the rate of a known lower-bound. The two keys to our improved proof technique are (1) a more precise upper- and lower-bound on the system Gram matrix and (2) a self-bounding argument for the expected estimation error of the optimal controller.

Exact Asymptotics for Linear Quadratic Adaptive Control

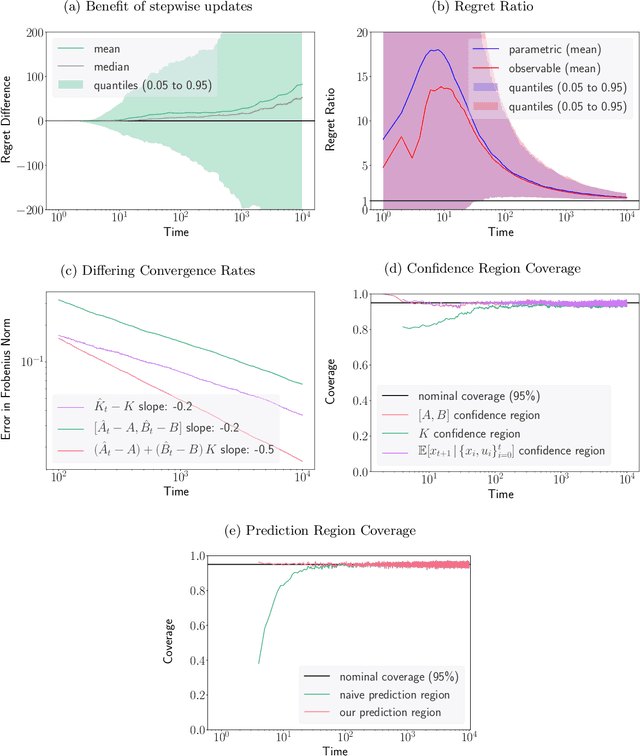
Recent progress in reinforcement learning has led to remarkable performance in a range of applications, but its deployment in high-stakes settings remains quite rare. One reason is a limited understanding of the behavior of reinforcement algorithms, both in terms of their regret and their ability to learn the underlying system dynamics---existing work is focused almost exclusively on characterizing rates, with little attention paid to the constants multiplying those rates that can be critically important in practice. To start to address this challenge, we study perhaps the simplest non-bandit reinforcement learning problem: linear quadratic adaptive control (LQAC). By carefully combining recent finite-sample performance bounds for the LQAC problem with a particular (less-recent) martingale central limit theorem, we are able to derive asymptotically-exact expressions for the regret, estimation error, and prediction error of a rate-optimal stepwise-updating LQAC algorithm. In simulations on both stable and unstable systems, we find that our asymptotic theory also describes the algorithm's finite-sample behavior remarkably well.

The Expressive Power of Neural Networks: A View from the Width

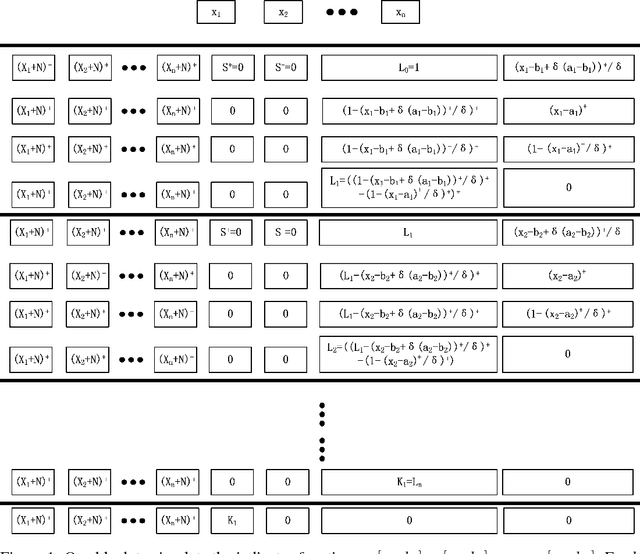
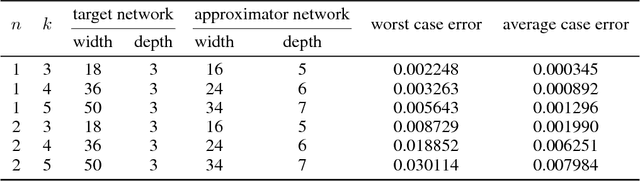
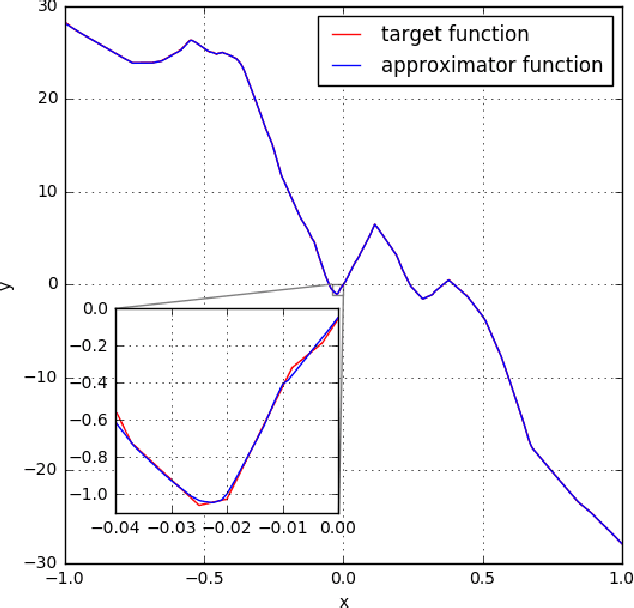
The expressive power of neural networks is important for understanding deep learning. Most existing works consider this problem from the view of the depth of a network. In this paper, we study how width affects the expressiveness of neural networks. Classical results state that depth-bounded (e.g. depth-$2$) networks with suitable activation functions are universal approximators. We show a universal approximation theorem for width-bounded ReLU networks: width-$(n+4)$ ReLU networks, where $n$ is the input dimension, are universal approximators. Moreover, except for a measure zero set, all functions cannot be approximated by width-$n$ ReLU networks, which exhibits a phase transition. Several recent works demonstrate the benefits of depth by proving the depth-efficiency of neural networks. That is, there are classes of deep networks which cannot be realized by any shallow network whose size is no more than an exponential bound. Here we pose the dual question on the width-efficiency of ReLU networks: Are there wide networks that cannot be realized by narrow networks whose size is not substantially larger? We show that there exist classes of wide networks which cannot be realized by any narrow network whose depth is no more than a polynomial bound. On the other hand, we demonstrate by extensive experiments that narrow networks whose size exceed the polynomial bound by a constant factor can approximate wide and shallow network with high accuracy. Our results provide more comprehensive evidence that depth is more effective than width for the expressiveness of ReLU networks.