Mitigating Forgetting in LLM Supervised Fine-Tuning and Preference Learning

Post-training of pre-trained LLMs, which typically consists of the supervised fine-tuning (SFT) stage and the preference learning (RLHF or DPO) stage, is crucial to effective and safe LLM applications. The widely adopted approach in post-training popular open-source LLMs is to sequentially perform SFT and RLHF/DPO. However, sequential training is sub-optimal in terms of SFT and RLHF/DPO trade-off: the LLM gradually forgets about the first stage's training when undergoing the second stage's training. We theoretically prove the sub-optimality of sequential post-training. Furthermore, we propose a practical joint post-training framework with theoretical convergence guarantees and empirically outperforms sequential post-training framework, while having similar computational cost. Our code is available at https://github.com/heshandevaka/XRIGHT.

Three-Way Trade-Off in Multi-Objective Learning: Optimization, Generalization and Conflict-Avoidance

Multi-objective learning (MOL) problems often arise in emerging machine learning problems when there are multiple learning criteria or multiple learning tasks. Recent works have developed various dynamic weighting algorithms for MOL such as MGDA and its variants, where the central idea is to find an update direction that avoids conflicts among objectives. Albeit its appealing intuition, empirical studies show that dynamic weighting methods may not always outperform static ones. To understand this theory-practical gap, we focus on a new stochastic variant of MGDA - the Multi-objective gradient with Double sampling (MoDo) algorithm, and study the generalization performance of the dynamic weighting-based MoDo and its interplay with optimization through the lens of algorithm stability. Perhaps surprisingly, we find that the key rationale behind MGDA -- updating along conflict-avoidant direction - may hinder dynamic weighting algorithms from achieving the optimal ${\cal O}(1/\sqrt{n})$ population risk, where $n$ is the number of training samples. We further demonstrate the variability of dynamic weights on the three-way trade-off among optimization, generalization, and conflict avoidance that is unique in MOL.

Mitigating Gradient Bias in Multi-objective Learning: A Provably Convergent Stochastic Approach

Machine learning problems with multiple objective functions appear either in learning with multiple criteria where learning has to make a trade-off between multiple performance metrics such as fairness, safety and accuracy; or, in multi-task learning where multiple tasks are optimized jointly, sharing inductive bias between them. This problems are often tackled by the multi-objective optimization framework. However, existing stochastic multi-objective gradient methods and its variants (e.g., MGDA, PCGrad, CAGrad, etc.) all adopt a biased noisy gradient direction, which leads to degraded empirical performance. To this end, we develop a stochastic Multi-objective gradient Correction (MoCo) method for multi-objective optimization. The unique feature of our method is that it can guarantee convergence without increasing the batch size even in the non-convex setting. Simulations on multi-task supervised and reinforcement learning demonstrate the effectiveness of our method relative to state-of-the-art methods.

On the Stability Analysis of Open Federated Learning Systems

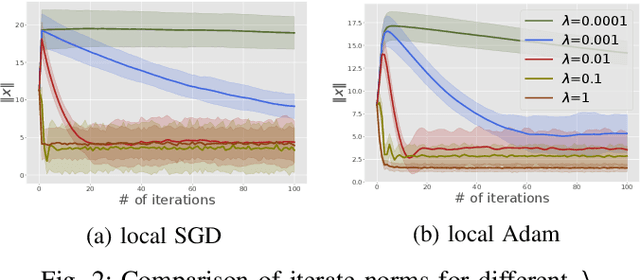
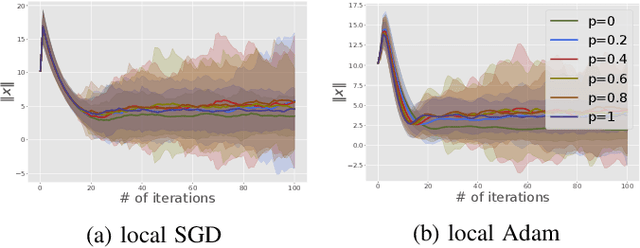
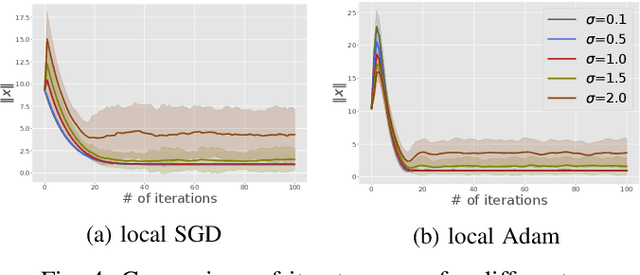
We consider the open federated learning (FL) systems, where clients may join and/or leave the system during the FL process. Given the variability of the number of present clients, convergence to a fixed model cannot be guaranteed in open systems. Instead, we resort to a new performance metric that we term the stability of open FL systems, which quantifies the magnitude of the learned model in open systems. Under the assumption that local clients' functions are strongly convex and smooth, we theoretically quantify the radius of stability for two FL algorithms, namely local SGD and local Adam. We observe that this radius relies on several key parameters, including the function condition number as well as the variance of the stochastic gradient. Our theoretical results are further verified by numerical simulations on both synthetic and real-world benchmark data-sets.