Classification by Separating Hypersurfaces: An Entropic Approach

We consider the following classification problem: Given a population of individuals characterized by a set of attributes represented as a vector in ${\mathbb R}^N$, the goal is to find a hyperplane in ${\mathbb R}^N$ that separates two sets of points corresponding to two distinct classes. This problem, with a history dating back to the perceptron model, remains central to machine learning. In this paper we propose a novel approach by searching for a vector of parameters in a bounded $N$-dimensional hypercube centered at the origin and a positive vector in ${\mathbb R}^M$, obtained through the minimization of an entropy-based function defined over the space of unknown variables. The method extends to polynomial surfaces, allowing the separation of data points by more complex decision boundaries. This provides a robust alternative to traditional linear or quadratic optimization techniques, such as support vector machines and gradient descent. Numerical experiments demonstrate the efficiency and versatility of the method in handling diverse classification tasks, including linear and non-linear separability.

Geometry and clustering with metrics derived from separable Bregman divergences

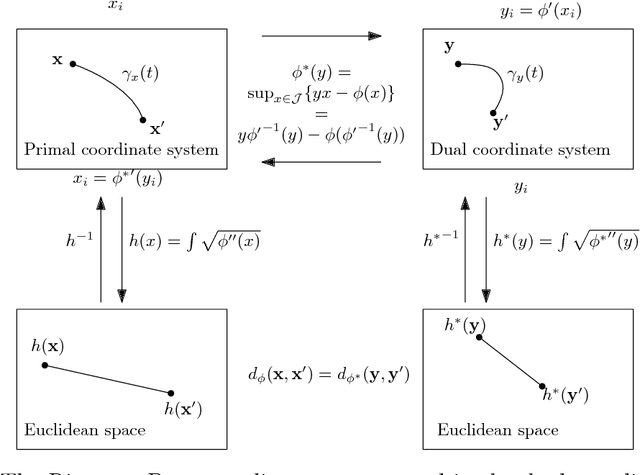
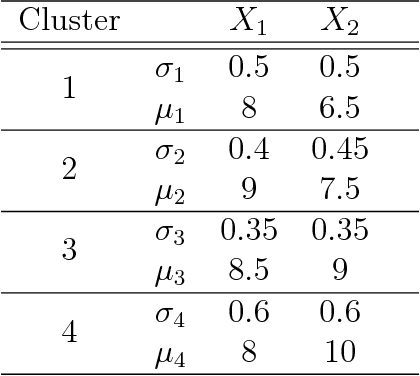
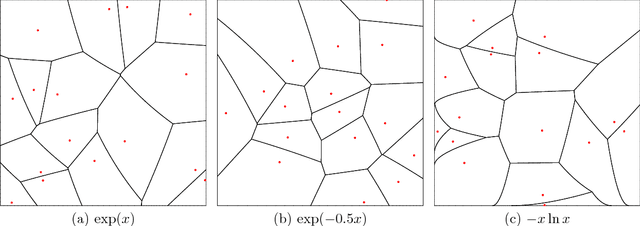
Separable Bregman divergences induce Riemannian metric spaces that are isometric to the Euclidean space after monotone embeddings. We investigate fixed rate quantization and its codebook Voronoi diagrams, and report on experimental performances of partition-based, hierarchical, and soft clustering algorithms with respect to these Riemann-Bregman distances.

Filtering Additive Measurement Noise with Maximum Entropy in the Mean

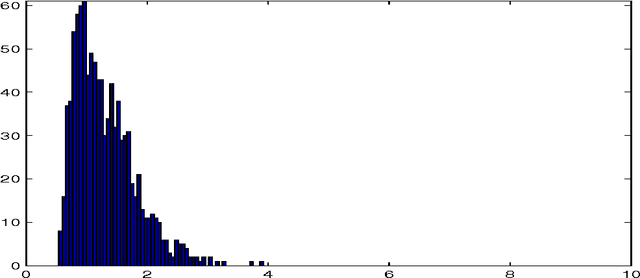
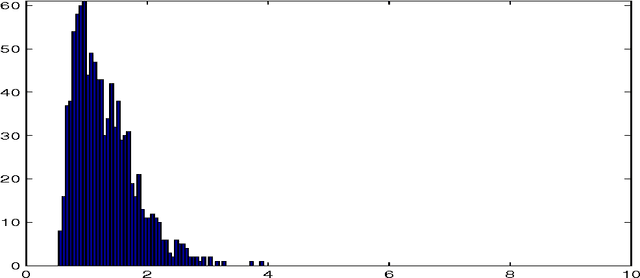
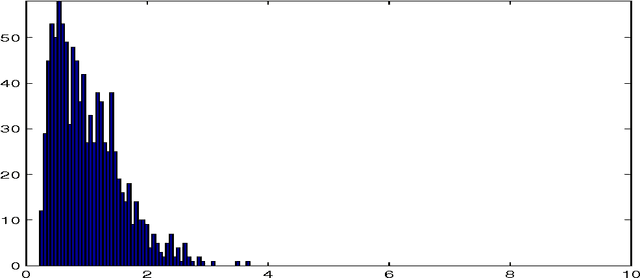
The purpose of this note is to show how the method of maximum entropy in the mean (MEM) may be used to improve parametric estimation when the measurements are corrupted by large level of noise. The method is developed in the context on a concrete example: that of estimation of the parameter in an exponential distribution. We compare the performance of our method with the bayesian and maximum likelihood approaches.