Classification by Separating Hypersurfaces: An Entropic Approach

We consider the following classification problem: Given a population of individuals characterized by a set of attributes represented as a vector in ${\mathbb R}^N$, the goal is to find a hyperplane in ${\mathbb R}^N$ that separates two sets of points corresponding to two distinct classes. This problem, with a history dating back to the perceptron model, remains central to machine learning. In this paper we propose a novel approach by searching for a vector of parameters in a bounded $N$-dimensional hypercube centered at the origin and a positive vector in ${\mathbb R}^M$, obtained through the minimization of an entropy-based function defined over the space of unknown variables. The method extends to polynomial surfaces, allowing the separation of data points by more complex decision boundaries. This provides a robust alternative to traditional linear or quadratic optimization techniques, such as support vector machines and gradient descent. Numerical experiments demonstrate the efficiency and versatility of the method in handling diverse classification tasks, including linear and non-linear separability.

Identifying bias in cluster quality metrics

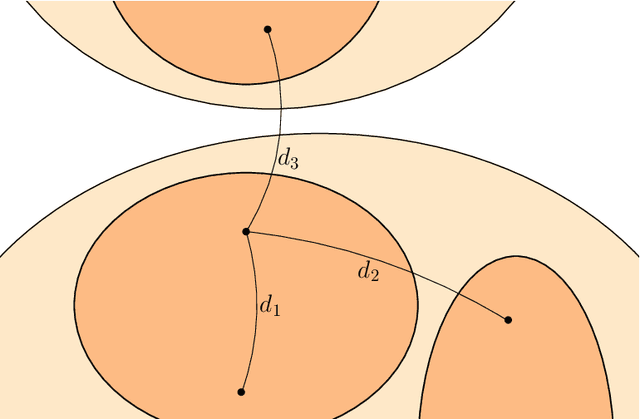
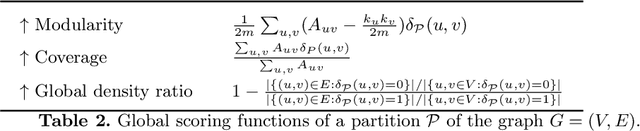
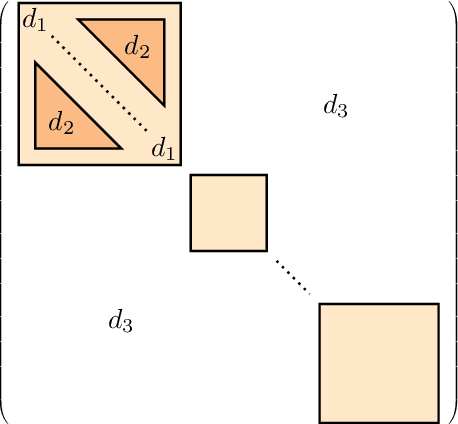
We study potential biases of popular cluster quality metrics, such as conductance or modularity. We propose a method that uses both stochastic and preferential attachment block models construction to generate networks with preset community structures, to which quality metrics will be applied. These models also allow us to generate multi-level structures of varying strength, which will show if metrics favour partitions into a larger or smaller number of clusters. Additionally, we propose another quality metric, the density ratio. We observed that most of the studied metrics tend to favour partitions into a smaller number of big clusters, even when their relative internal and external connectivity are the same. The metrics found to be less biased are modularity and density ratio.