Categorical Belief Propagation: Sheaf-Theoretic Inference via Descent and Holonomy

We develop a categorical foundation for belief propagation on factor graphs. We construct the free hypergraph category \(\Syn_Σ\) on a typed signature and prove its universal property, yielding compositional semantics via a unique functor to the matrix category \(\cat{Mat}_R\). Message-passing is formulated using a Grothendieck fibration \(\int\Msg \to \cat{FG}_Σ\) over polarized factor graphs, with schedule-indexed endomorphisms defining BP updates. We characterize exact inference as effective descent: local beliefs form a descent datum when compatibility conditions hold on overlaps. This framework unifies tree exactness, junction tree algorithms, and loopy BP failures under sheaf-theoretic obstructions. We introduce HATCC (Holonomy-Aware Tree Compilation), an algorithm that detects descent obstructions via holonomy computation on the factor nerve, compiles non-trivial holonomy into mode variables, and reduces to tree BP on an augmented graph. Complexity is \(O(n^2 d_{\max} + c \cdot k_{\max} \cdot δ_{\max}^3 + n \cdot δ_{\max}^2)\) for \(n\) factors and \(c\) fundamental cycles. Experimental results demonstrate exact inference with significant speedup over junction trees on grid MRFs and random graphs, along with UNSAT detection on satisfiability instances.

Filtering Additive Measurement Noise with Maximum Entropy in the Mean

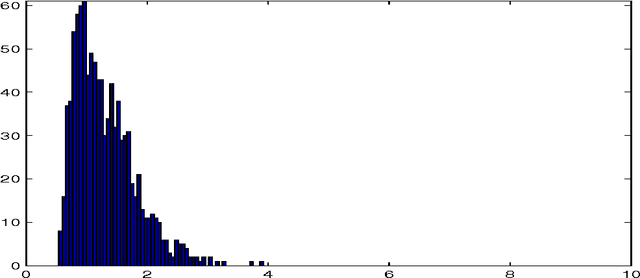
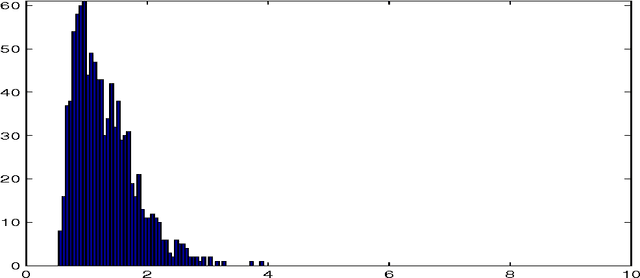
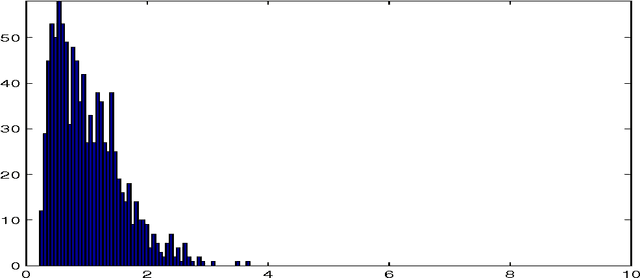
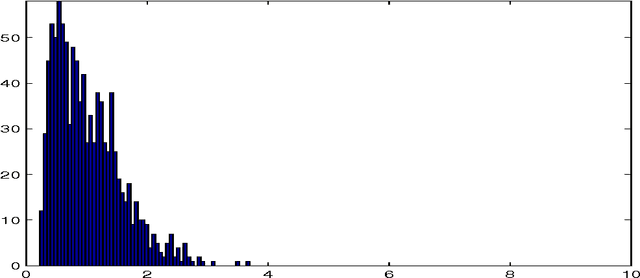
The purpose of this note is to show how the method of maximum entropy in the mean (MEM) may be used to improve parametric estimation when the measurements are corrupted by large level of noise. The method is developed in the context on a concrete example: that of estimation of the parameter in an exponential distribution. We compare the performance of our method with the bayesian and maximum likelihood approaches.