Simplifying Adversarially Robust PAC Learning with Tolerance

Adversarially robust PAC learning has proved to be challenging, with the currently best known learners [Montasser et al., 2021a] relying on improper methods based on intricate compression schemes, resulting in sample complexity exponential in the VC-dimension. A series of follow up work considered a slightly relaxed version of the problem called adversarially robust learning with tolerance [Ashtiani et al., 2023, Bhattacharjee et al., 2023, Raman et al., 2024] and achieved better sample complexity in terms of the VC-dimension. However, those algorithms were either improper and complex, or required additional assumptions on the hypothesis class H. We prove, for the first time, the existence of a simpler learner that achieves a sample complexity linear in the VC-dimension without requiring additional assumptions on H. Even though our learner is improper, it is "almost proper" in the sense that it outputs a hypothesis that is "similar" to a hypothesis in H. We also use the ideas from our algorithm to construct a semi-supervised learner in the tolerant setting. This simple algorithm achieves comparable bounds to the previous (non-tolerant) semi-supervised algorithm of Attias et al. [2022a], but avoids the use of intricate subroutines from previous works, and is "almost proper."

On the Computability of Multiclass PAC Learning

We study the problem of computable multiclass learnability within the Probably Approximately Correct (PAC) learning framework of Valiant (1984). In the recently introduced computable PAC (CPAC) learning framework of Agarwal et al. (2020), both learners and the functions they output are required to be computable. We focus on the case of finite label space and start by proposing a computable version of the Natarajan dimension and showing that it characterizes CPAC learnability in this setting. We further generalize this result by establishing a meta-characterization of CPAC learnability for a certain family of dimensions: computable distinguishers. Distinguishers were defined by Ben-David et al. (1992) as a certain family of embeddings of the label space, with each embedding giving rise to a dimension. It was shown that the finiteness of each such dimension characterizes multiclass PAC learnability for finite label space in the non-computable setting. We show that the corresponding computable dimensions for distinguishers characterize CPAC learning. We conclude our analysis by proving that the DS dimension, which characterizes PAC learnability for infinite label space, cannot be expressed as a distinguisher (even in the case of finite label space).

Calibration through the Lens of Interpretability

Calibration is a frequently invoked concept when useful label probability estimates are required on top of classification accuracy. A calibrated model is a function whose values correctly reflect underlying label probabilities. Calibration in itself however does not imply classification accuracy, nor human interpretable estimates, nor is it straightforward to verify calibration from finite data. There is a plethora of evaluation metrics (and loss functions) that each assess a specific aspect of a calibration model. In this work, we initiate an axiomatic study of the notion of calibration. We catalogue desirable properties of calibrated models as well as corresponding evaluation metrics and analyze their feasibility and correspondences. We complement this analysis with an empirical evaluation, comparing common calibration methods to employing a simple, interpretable decision tree.

On the Computability of Robust PAC Learning

We initiate the study of computability requirements for adversarially robust learning. Adversarially robust PAC-type learnability is by now an established field of research. However, the effects of computability requirements in PAC-type frameworks are only just starting to emerge. We introduce the problem of robust computable PAC (robust CPAC) learning and provide some simple sufficient conditions for this. We then show that learnability in this setup is not implied by the combination of its components: classes that are both CPAC and robustly PAC learnable are not necessarily robustly CPAC learnable. Furthermore, we show that the novel framework exhibits some surprising effects: for robust CPAC learnability it is not required that the robust loss is computably evaluable! Towards understanding characterizing properties, we introduce a novel dimension, the computable robust shattering dimension. We prove that its finiteness is necessary, but not sufficient for robust CPAC learnability. This might yield novel insights for the corresponding phenomenon in the context of robust PAC learnability, where insufficiency of the robust shattering dimension for learnability has been conjectured, but so far a resolution has remained elusive.

Learning Losses for Strategic Classification

Strategic classification, i.e. classification under possible strategic manipulations of features, has received a lot of attention from both the machine learning and the game theory community. Most works focus on analysing properties of the optimal decision rule under such manipulations. In our work we take a learning theoretic perspective, focusing on the sample complexity needed to learn a good decision rule which is robust to strategic manipulation. We perform this analysis by introducing a novel loss function, the \emph{strategic manipulation loss}, which takes into account both the accuracy of the final decision rule and its vulnerability to manipulation. We analyse the sample complexity for a known graph of possible manipulations in terms of the complexity of the function class and the manipulation graph. Additionally, we initialize the study of learning under unknown manipulation capabilities of the involved agents. Using techniques from transfer learning theory, we define a similarity measure for manipulation graphs and show that learning outcomes are robust with respect to small changes in the manipulation graph. Lastly, we analyse the (sample complexity of) learning of the manipulation capability of agents with respect to this similarity measure, providing novel guarantees for strategic classification with respect to an unknown manipulation graph.

Adversarially Robust Learning with Tolerance

We study the problem of tolerant adversarial PAC learning with respect to metric perturbation sets. In adversarial PAC learning, an adversary is allowed to replace a test point $x$ with an arbitrary point in a closed ball of radius $r$ centered at $x$. In the tolerant version, the error of the learner is compared with the best achievable error with respect to a slightly larger perturbation radius $(1+\gamma)r$. For perturbation sets with doubling dimension $d$, we show that a variant of the natural ``perturb-and-smooth'' algorithm PAC learns any hypothesis class $\mathcal{H}$ with VC dimension $v$ in the $\gamma$-tolerant adversarial setting with $O\left(\frac{v(1+1/\gamma)^{O(d)}}{\varepsilon}\right)$ samples. This is the first such general guarantee with linear dependence on $v$ even for the special case where the domain is the real line and the perturbation sets are closed balls (intervals) of radius $r$. However, the proposed guarantees for the perturb-and-smooth algorithm currently only hold in the tolerant robust realizable setting and exhibit exponential dependence on $d$. We additionally propose an alternative learning method which yields sample complexity bounds with only linear dependence on the doubling dimension even in the more general agnostic case. This approach is based on sample compression.

On the (Un-)Avoidability of Adversarial Examples

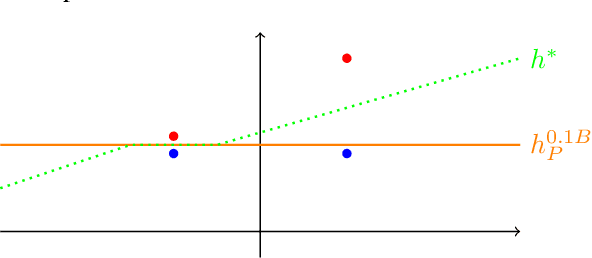
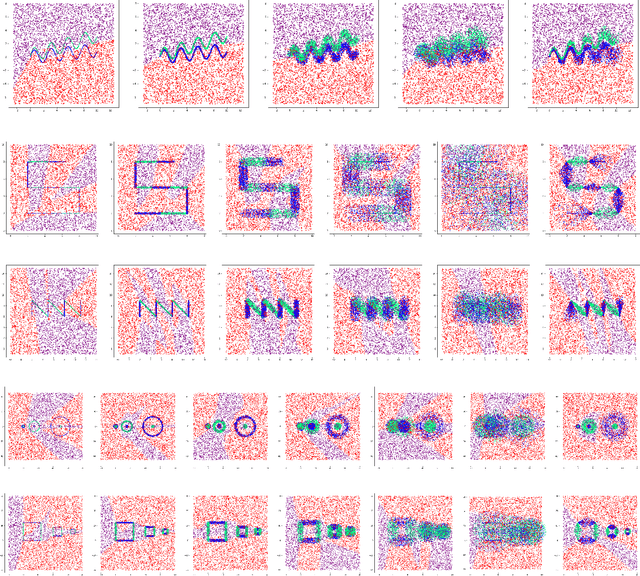
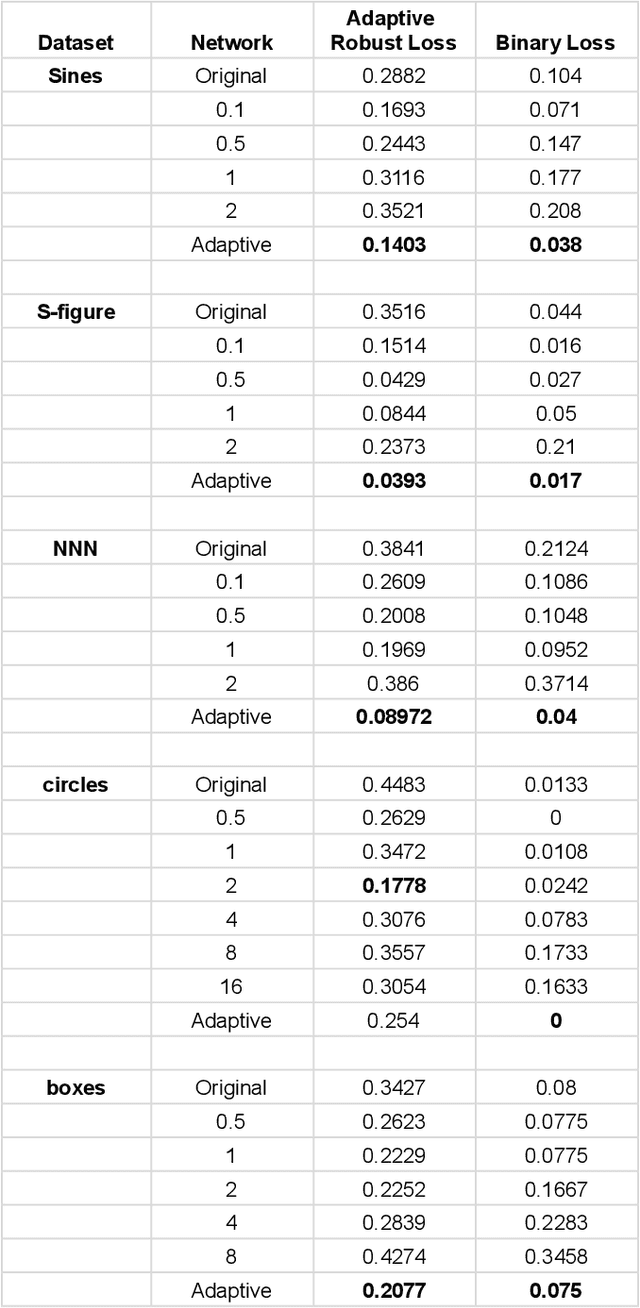
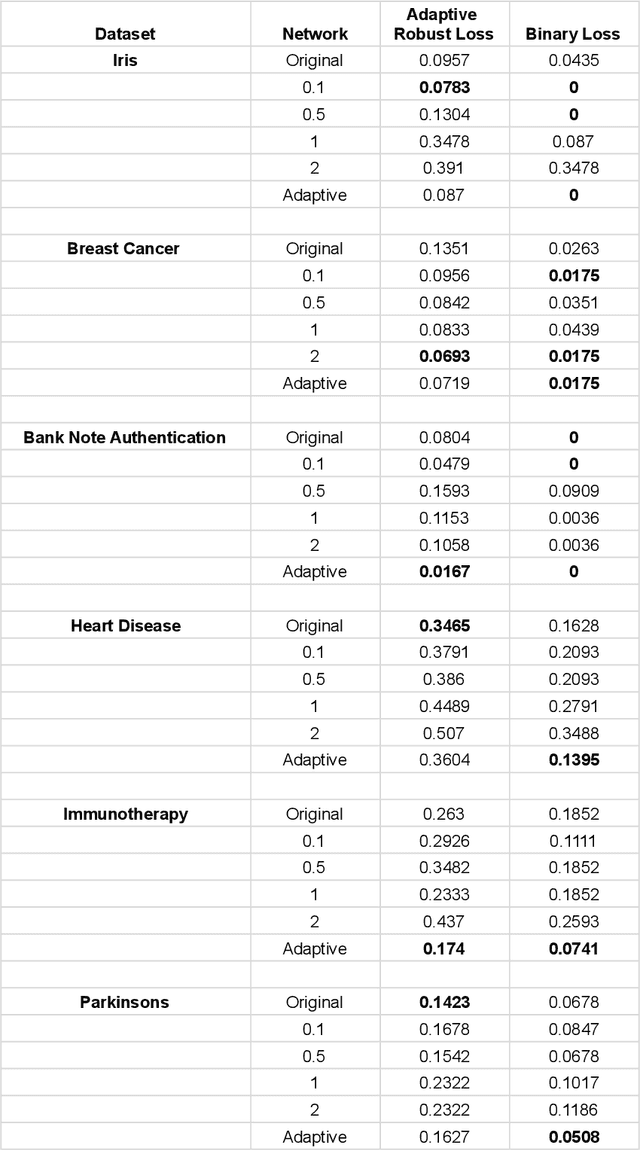
The phenomenon of adversarial examples in deep learning models has caused substantial concern over their reliability. While many deep neural networks have shown impressive performance in terms of predictive accuracy, it has been shown that in many instances an imperceptible perturbation can falsely flip the network's prediction. Most research has then focused on developing defenses against adversarial attacks or learning under a worst-case adversarial loss. In this work, we take a step back and aim to provide a framework for determining whether a model's label change under small perturbation is justified (and when it is not). We carefully argue that adversarial robustness should be defined as a locally adaptive measure complying with the underlying distribution. We then suggest a definition for an adaptive robust loss, derive an empirical version of it, and develop a resulting data-augmentation framework. We prove that our adaptive data-augmentation maintains consistency of 1-nearest neighbor classification under deterministic labels and provide illustrative empirical evaluations.

Black-box Certification and Learning under Adversarial Perturbations

We formally study the problem of classification under adversarial perturbations, both from the learner's perspective, and from the viewpoint of a third-party who aims at certifying the robustness of a given black-box classifier. We analyze a PAC-type framework of semi-supervised learning and identify possibility and impossibility results for proper learning of VC-classes in this setting. We further introduce and study a new setting of black-box certification under limited query budget. We analyze this for various classes of predictors and types of perturbation. We also consider the viewpoint of a black-box adversary that aims at finding adversarial examples, showing that the existence of an adversary with polynomial query complexity implies the existence of a robust learner with small sample complexity.

When can unlabeled data improve the learning rate?

In semi-supervised classification, one is given access both to labeled and unlabeled data. As unlabeled data is typically cheaper to acquire than labeled data, this setup becomes advantageous as soon as one can exploit the unlabeled data in order to produce a better classifier than with labeled data alone. However, the conditions under which such an improvement is possible are not fully understood yet. Our analysis focuses on improvements in the minimax learning rate in terms of the number of labeled examples (with the number of unlabeled examples being allowed to depend on the number of labeled ones). We argue that for such improvements to be realistic and indisputable, certain specific conditions should be satisfied and previous analyses have failed to meet those conditions. We then demonstrate examples where these conditions can be met, in particular showing rate changes from $1/\sqrt{\ell}$ to $e^{-c\ell}$ and from $1/\sqrt{\ell}$ to $1/\ell$. These results improve our understanding of what is and isn't possible in semi-supervised learning.

Active Nearest-Neighbor Learning in Metric Spaces

We propose a pool-based non-parametric active learning algorithm for general metric spaces, called MArgin Regularized Metric Active Nearest Neighbor (MARMANN), which outputs a nearest-neighbor classifier. We give prediction error guarantees that depend on the noisy-margin properties of the input sample, and are competitive with those obtained by previously proposed passive learners. We prove that the label complexity of MARMANN is significantly lower than that of any passive learner with similar error guarantees. MARMANN is based on a generalized sample compression scheme, and a new label-efficient active model-selection procedure.