Fractional-Boundary-Regularized Deep Galerkin Method for Variational Inequalities in Mixed Optimal Stopping and Control

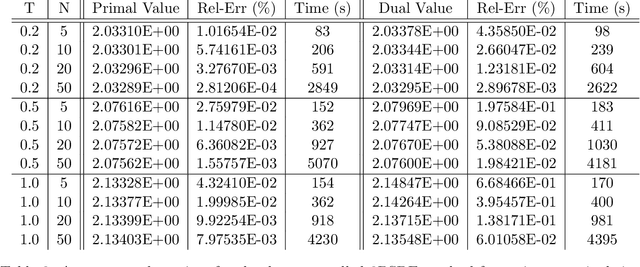
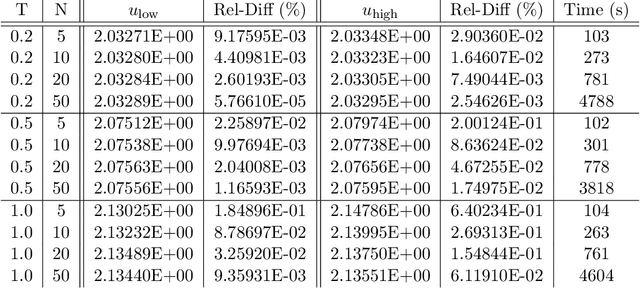
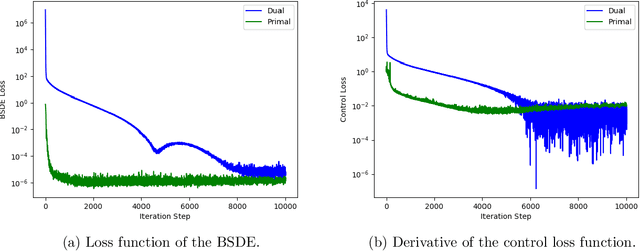
Mixed optimal stopping and stochastic control problems define variational inequalities with non-linear Hamilton-Jacobi-Bellman (HJB) operators, whose numerical solution is notoriously difficult and lack of reliable benchmarks. We first use the dual approach to transform it into a linear operator, and then introduce a Fractional-Boundary-Regularized Deep Galerkin Method (FBR-DGM) that augments the classical $L^2$ loss with Sobolev-Slobodeckij norms on the parabolic boundary, enforcing regularity and yielding consistent improvements in the network approximation and its derivatives. The improved accuracy allows the network to be converted back to the original solution using the dual transform. The self-consistency and stability of the network can be tested by checking the primal-dual relationship among optimal value, optimal wealth, and optimal control, offering innovative benchmarks in the absence of analytical solutions.

Step-wise Adaptive Integration of Supervised Fine-tuning and Reinforcement Learning for Task-Specific LLMs

Large language models (LLMs) excel at mathematical reasoning and logical problem-solving. The current popular training paradigms primarily use supervised fine-tuning (SFT) and reinforcement learning (RL) to enhance the models' reasoning abilities. However, when using SFT or RL alone, there are respective challenges: SFT may suffer from overfitting, while RL is prone to mode collapse. The state-of-the-art methods have proposed hybrid training schemes. However, static switching faces challenges such as poor generalization across different tasks and high dependence on data quality. In response to these challenges, inspired by the curriculum learning-quiz mechanism in human reasoning cultivation, We propose SASR, a step-wise adaptive hybrid training framework that theoretically unifies SFT and RL and dynamically balances the two throughout optimization. SASR uses SFT for initial warm-up to establish basic reasoning skills, and then uses an adaptive dynamic adjustment algorithm based on gradient norm and divergence relative to the original distribution to seamlessly integrate SFT with the online RL method GRPO. By monitoring the training status of LLMs and adjusting the training process in sequence, SASR ensures a smooth transition between training schemes, maintaining core reasoning abilities while exploring different paths. Experimental results demonstrate that SASR outperforms SFT, RL, and static hybrid training methods.

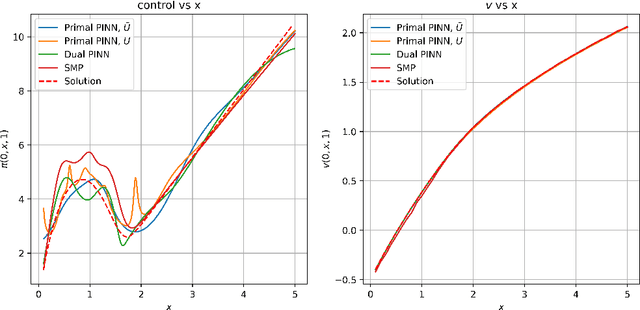
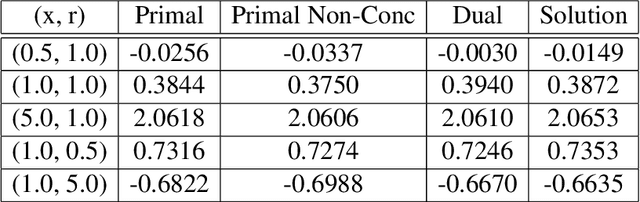
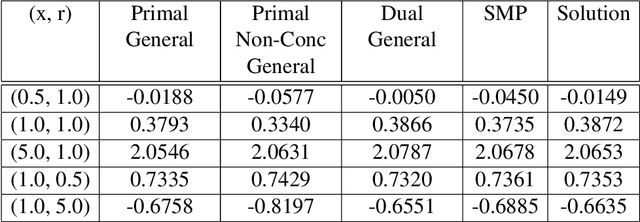
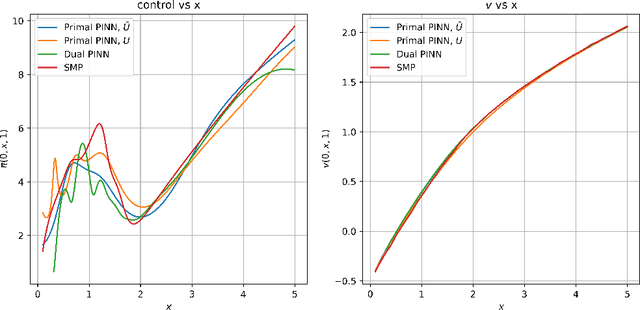
Deep Learning Methods for S Shaped Utility Maximisation with a Random Reference Point

We consider the portfolio optimisation problem where the terminal function is an S-shaped utility applied at the difference between the wealth and a random benchmark process. We develop several numerical methods for solving the problem using deep learning and duality methods. We use deep learning methods to solve the associated Hamilton-Jacobi-Bellman equation for both the primal and dual problems, and the adjoint equation arising from the stochastic maximum principle. We compare the solution of this non-concave problem to that of concavified utility, a random function depending on the benchmark, in both complete and incomplete markets. We give some numerical results for power and log utilities to show the accuracy of the suggested algorithms.

Deep Learning for Constrained Utility Maximisation

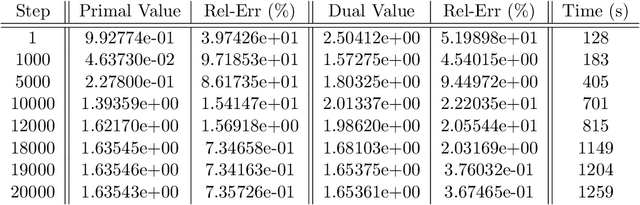
This paper proposes two algorithms for solving stochastic control problems with deep reinforcement learning, with a focus on the utility maximisation problem. The first algorithm solves Markovian problems via the Hamilton Jacobi Bellman (HJB) equation. We solve this highly nonlinear partial differential equation (PDE) with a second order backward stochastic differential equation (2BSDE) formulation. The convex structure of the problem allows us to describe a dual problem that can either verify the original primal approach or bypass some of the complexity. The second algorithm utilises the full power of the duality method to solve non-Markovian problems, which are often beyond the scope of stochastic control solvers in the existing literature. We solve an adjoint BSDE that satisfies the dual optimality conditions. We apply these algorithms to problems with power, log and non-HARA utilities in the Black-Scholes, the Heston stochastic volatility, and path dependent volatility models. Numerical experiments show highly accurate results with low computational cost, supporting our proposed algorithms.