Neural Network Approximation: Three Hidden Layers Are Enough

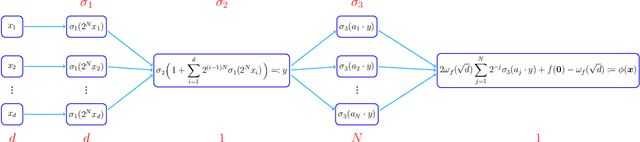
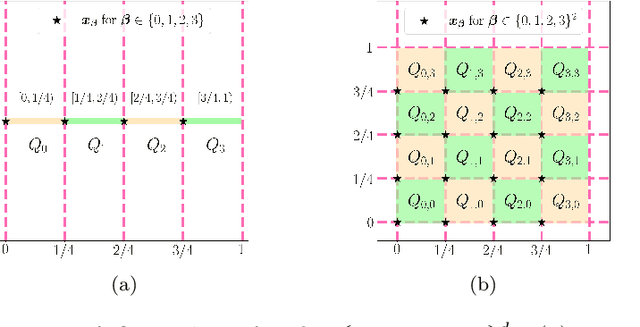
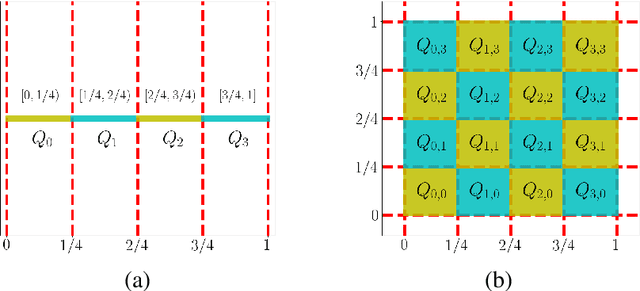
A three-hidden-layer neural network with super approximation power is introduced. This network is built with the Floor function ($\lfloor x\rfloor$), the exponential function ($2^x$), the step function ($\one_{x\geq 0}$), or their compositions as activation functions in each neuron and hence we call such networks as Floor-Exponential-Step (FLES) networks. For any width hyper-parameter $N\in\mathbb{N}^+$, it is shown that FLES networks with a width $\max\{d,\, N\}$ and three hidden layers can uniformly approximate a H{\"o}lder function $f$ on $[0,1]^d$ with an exponential approximation rate $3\lambda d^{\alpha/2}2^{-\alpha N}$, where $\alpha \in(0,1]$ and $\lambda$ are the H{\"o}lder order and constant, respectively. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the constructive approximation rate is $\omega_f(\sqrt{d}\,2^{-N})+2\omega_f(\sqrt{d}){2^{-N}}$. As a consequence, this new {class of networks} overcomes the curse of dimensionality in approximation power when the variation of $\omega_f(r)$ as $r\rightarrow 0$ is moderate (e.g., $\omega_f(r){\lesssim} r^\alpha$ for H{\"o}lder continuous functions), since the major term to be concerned in our approximation rate is essentially $\sqrt{d}$ times a function of $N$ independent of $d$ within the modulus of continuity.

Two-Layer Neural Networks for Partial Differential Equations: Optimization and Generalization Theory

Deep learning has significantly revolutionized the design of numerical algorithms for solving high-dimensional partial differential equations (PDEs). Yet the empirical successes of such approaches remains mysterious in theory. In deep learning-based PDE solvers, solving the original PDE is formulated into an expectation minimization problem with a PDE solution space discretized via deep neural networks. A global minimizer corresponds to a deep neural network that solves the given PDE. Typically, gradient descent-based methods are applied to minimize the expectation. This paper shows that gradient descent can identify a global minimizer of the optimization problem with a well-controlled generalization error in the case of two-layer neural networks in the over-parameterization regime (i.e., the network width is sufficiently large). The generalization error of the gradient descent solution does not suffer from the curse of dimensonality if the solution is in a Barron-type space. The theories developed here could form a theoretical foundation of deep learning-based PDE solvers.

Deep Network Approximation with Discrepancy Being Reciprocal of Width to Power of Depth

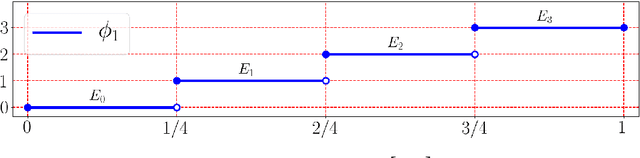
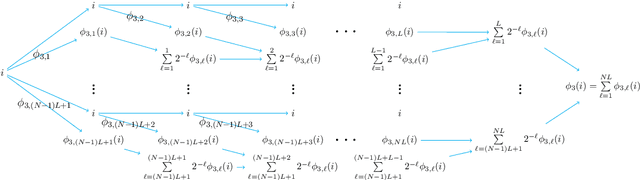
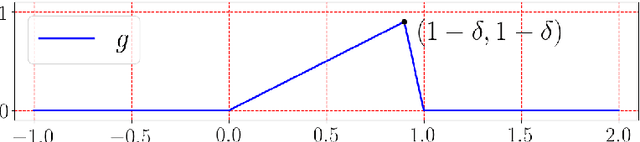
A new network with super approximation power is introduced. This network is built with Floor ($\lfloor x\rfloor$) and ReLU ($\max\{0,x\}$) activation functions and hence we call such networks as Floor-ReLU networks. It is shown by construction that Floor-ReLU networks with width $\max\{d,\, 5N+13\}$ and depth $64dL+3$ can pointwise approximate a Lipschitz continuous function $f$ on $[0,1]^d$ with an exponential approximation rate $3\mu\sqrt{d}\,N^{-\sqrt{L}}$, where $\mu$ is the Lipschitz constant of $f$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the constructive approximation rate is $\omega_f(\sqrt{d}\,N^{-\sqrt{L}})+2\omega_f(\sqrt{d}){N^{-\sqrt{L}}}$. As a consequence, this new network overcomes the curse of dimensionality in approximation power since this approximation order is essentially $\sqrt{d}$ times a function of $N$ and $L$ independent of $d$.

Deep Network Approximation for Smooth Functions

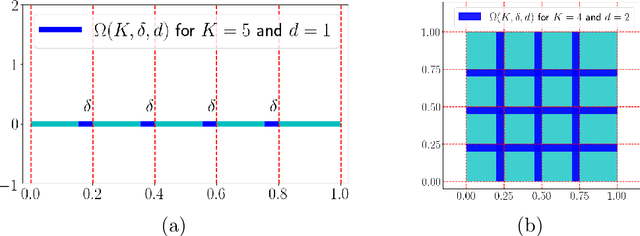
This paper establishes optimal approximation error characterization of deep ReLU networks for smooth functions in terms of both width and depth simultaneously. To that end, we first prove that multivariate polynomials can be approximated by deep ReLU networks of width $\mathcal{O}(N)$ and depth $\mathcal{O}(L)$ with an approximation error $\mathcal{O}(N^{-L})$. Through local Taylor expansions and their deep ReLU network approximations, we show that deep ReLU networks of width $\mathcal{O}(N\ln N)$ and depth $\mathcal{O}(L\ln L)$ can approximate $f\in C^s([0,1]^d)$ with a nearly optimal approximation rate $\mathcal{O}(\|f\|_{C^s([0,1]^d)}N^{-2s/d}L^{-2s/d})$. Our estimate is non-asymptotic in the sense that it is valid for arbitrary width and depth specified by $N\in\mathbb{N}^+$ and $L\in\mathbb{N}^+$, respectively.

Machine Learning for Prediction with Missing Dynamics

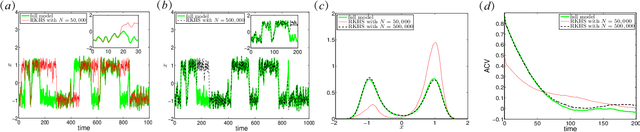
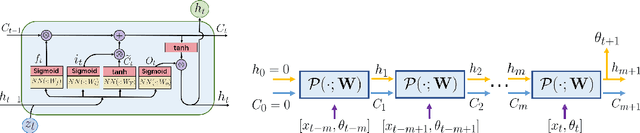
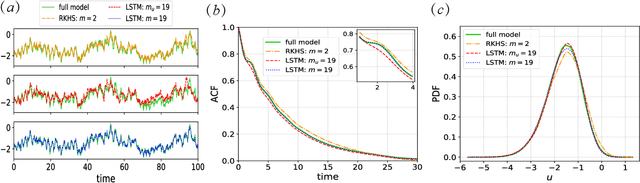
This article presents a general framework for recovering missing dynamical systems using available data and machine learning techniques. The proposed framework reformulates the prediction problem as a supervised learning problem to approximate a map that takes the memories of the resolved and identifiable unresolved variables to the missing components in the resolved dynamics. We demonstrate the effectiveness of the proposed framework with a theoretical guarantee of a path-wise convergence of the resolved variables up to finite time and numerical tests on prototypical models in various scientific domains. These include the 57-mode barotropic stress models with multiscale interactions that mimic the blocked and unblocked patterns observed in the atmosphere, the nonlinear Schr\"{o}dinger equation which found many applications in physics such as optics and Bose-Einstein-Condense, the Kuramoto-Sivashinsky equation which spatiotemporal chaotic pattern formation models trapped ion mode in plasma and phase dynamics in reaction-diffusion systems. While many machine learning techniques can be used to validate the proposed framework, we found that recurrent neural networks outperform kernel regression methods in terms of recovering the trajectory of the resolved components and the equilibrium one-point and two-point statistics. This superb performance suggests that recurrent neural networks are an effective tool for recovering the missing dynamics that involves approximation of high-dimensional functions.

Instance Enhancement Batch Normalization: an Adaptive Regulator of Batch Noise

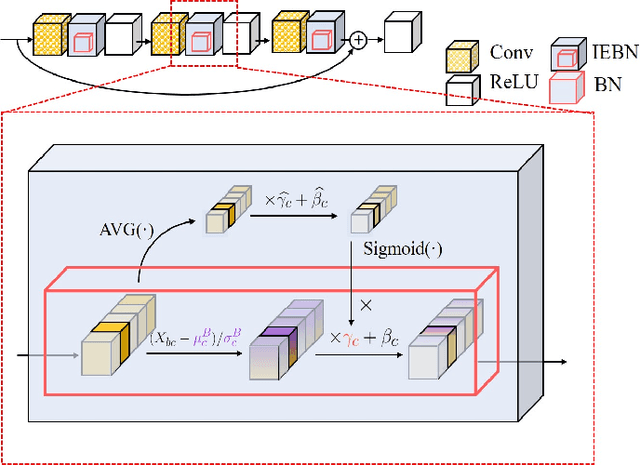
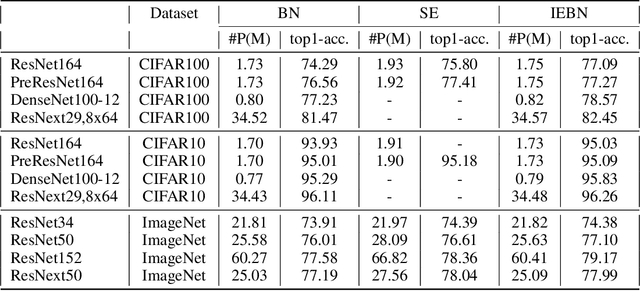
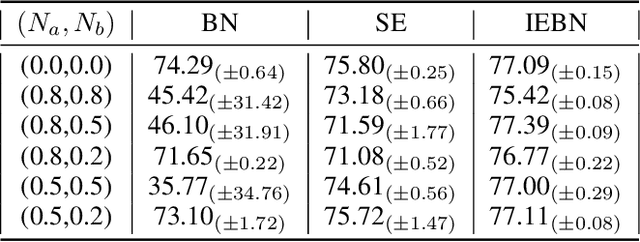
Batch Normalization (BN) (Ioffe and Szegedy 2015) normalizes the features of an input image via statistics of a batch of images and this batch information is considered as batch noise that will be brought to the features of an instance by BN. We offer a point of view that self-attention mechanism can help regulate the batch noise by enhancing instance-specific information. Based on this view, we propose combining BN with a self-attention mechanism to adjust the batch noise and give an attention-based version of BN called Instance Enhancement Batch Normalization (IEBN) which recalibrates channel information by a simple linear transformation. IEBN outperforms BN with a light parameter increment in various visual tasks universally for different network structures and benchmark data sets. Besides, even if under the attack of synthetic noise, IEBN can still stabilize network training with good generalization. The code of IEBN is available at https://github.com/gbup-group/IEBN

Error bounds for deep ReLU networks using the Kolmogorov--Arnold superposition theorem

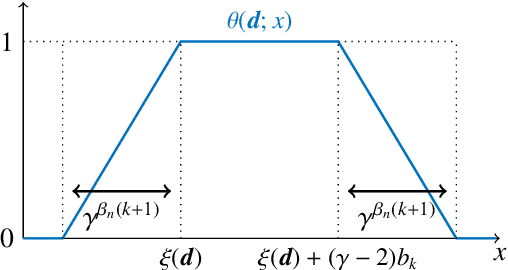
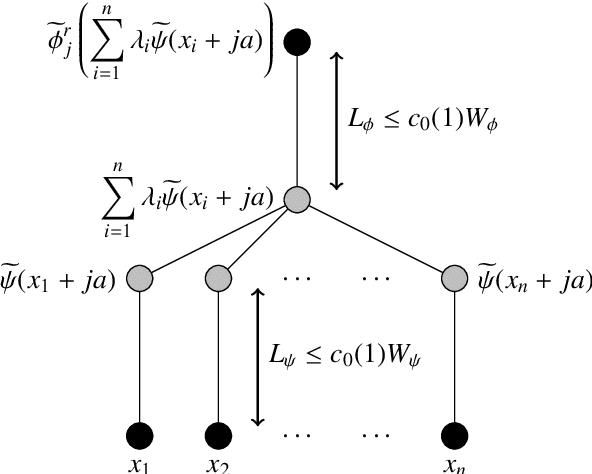
We prove a theorem concerning the approximation of multivariate continuous functions by deep ReLU networks, for which the curse of the dimensionality is lessened. Our theorem is based on the Kolmogorov--Arnold superposition theorem, and on the approximation of the inner and outer functions that appear in the superposition by very deep ReLU networks.

Deep Network Approximation Characterized by Number of Neurons

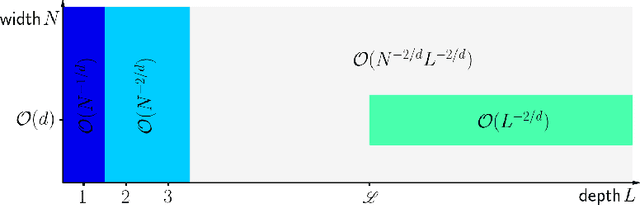
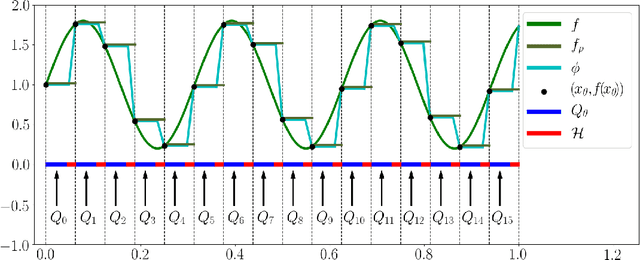
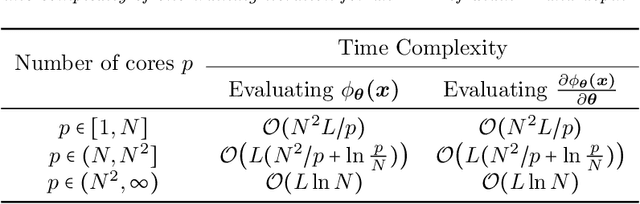
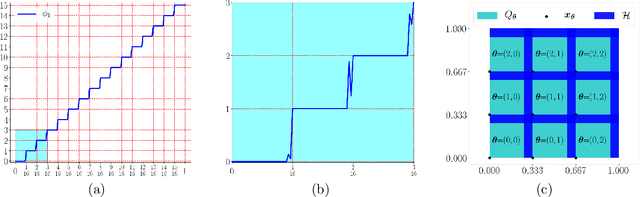
This paper quantitatively characterizes the approximation power of deep feed-forward neural networks (FNNs) in terms of the number of neurons, i.e., the product of the network width and depth. It is shown by construction that ReLU FNNs with width $\mywidth$ and depth $9L+12$ can approximate an arbitrary H\"older continuous function of order $\alpha$ with a Lipschitz constant $\nu$ on $[0,1]^d$ with a tight approximation rate $5(8\sqrt{d})^\alpha\nu N^{-2\alpha/d}L^{-2\alpha/d}$ for any given $N,L\in \N^+$. The constructive approximation is a corollary of a more general result for an arbitrary continuous function $f$ in terms of its modulus of continuity $\omega_f(\cdot)$. In particular, the approximation rate of ReLU FNNs with width $\mywidth$ and depth $9L+12$ for a general continuous function $f$ is $5\omega_f(8\sqrt{d} N^{-2/d}L^{-2/d})$. We also extend our analysis to the case when the domain of $f$ is irregular or localized in an $\epsilon$-neighborhood of a $d_{\mathcal{M}}$-dimensional smooth manifold $\mathcal{M}\subseteq [0,1]^d$ with $d_{\mathcal{M}}\ll d$. Especially, in the case of an essentially low-dimensional domain, we show an approximation rate $3\omega_f\big(\tfrac{4\epsilon}{1-\delta}\sqrt{\tfrac{d}{d_\delta}}\big)+5\omega_f\big(\tfrac{16d}{(1-\delta)\sqrt{d_\delta}}N^{-2/d_\delta}L^{-2/d_\delta }\big)$ for ReLU FNNs to approximate $f$ in the $\epsilon$-neighborhood, where $d_\delta=\OO\big(d_{\mathcal{M}}\tfrac{\ln (d/\delta)}{\delta^2}\big)$ for any given $\delta\in(0,1)$. Our analysis provides a general guide for selecting the width and the depth of ReLU FNNs to approximate continuous functions especially in parallel computing.

DIANet: Dense-and-Implicit Attention Network

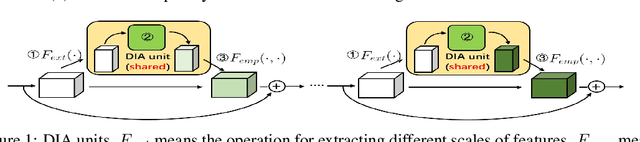
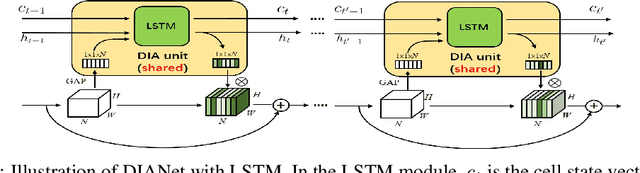
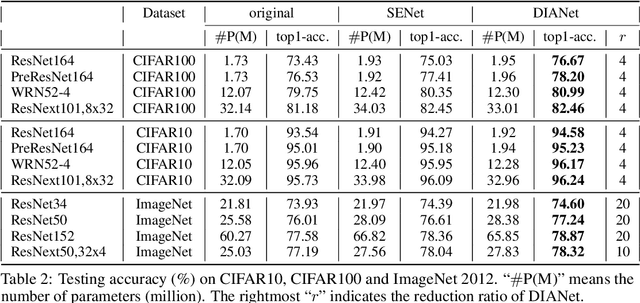
Attention-based deep neural networks (DNNs) that emphasize the informative information in a local receptive field of an input image have successfully boosted the performance of deep learning in various challenging problems. In this paper, we propose a Dense-and-Implicit-Attention (DIA) unit that can be applied universally to different network architectures and enhance their generalization capacity by repeatedly fusing the information throughout different network layers. The communication of information between different layers is carried out via a modified Long Short Term Memory (LSTM) module within the DIA unit that is in parallel with the DNN. The sharing DIA unit links multi-scale features from different depth levels of the network implicitly and densely. Experiments on benchmark datasets show that the DIA unit is capable of emphasizing channel-wise feature interrelation and leads to significant improvement of image classification accuracy. We further empirically show that the DIA unit is a nonlocal normalization tool that enhances the Batch Normalization. The code is released at https://github.com/gbup-group/DIANet.

CASS: Cross Adversarial Source Separation via Autoencoder

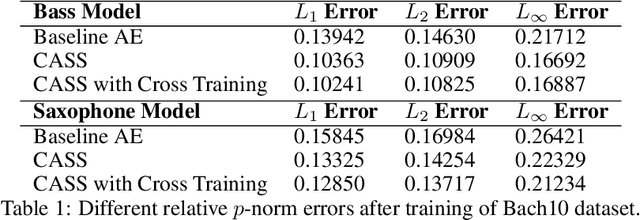
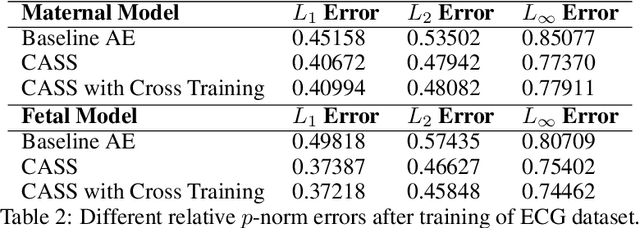
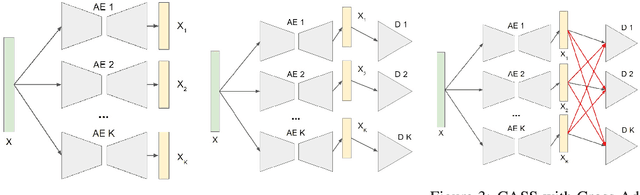
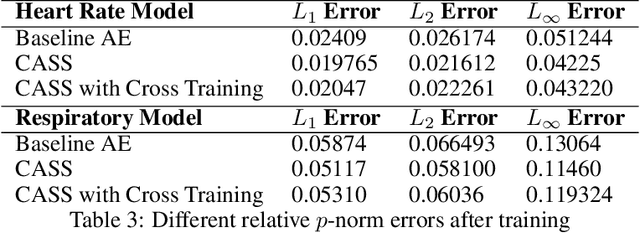
This paper introduces a cross adversarial source separation (CASS) framework via autoencoder, a new model that aims at separating an input signal consisting of a mixture of multiple components into individual components defined via adversarial learning and autoencoder fitting. CASS unifies popular generative networks like auto-encoders (AEs) and generative adversarial networks (GANs) in a single framework. The basic building block that filters the input signal and reconstructs the $i$-th target component is a pair of deep neural networks $\mathcal{EN}_i$ and $\mathcal{DE}_i$ as an encoder for dimension reduction and a decoder for component reconstruction, respectively. The decoder $\mathcal{DE}_i$ as a generator is enhanced by a discriminator network $\mathcal{D}_i$ that favors signal structures of the $i$-th component in the $i$-th given dataset as guidance through adversarial learning. In contrast with existing practices in AEs which trains each Auto-Encoder independently, or in GANs that share the same generator, we introduce cross adversarial training that emphasizes adversarial relation between any arbitrary network pairs $(\mathcal{DE}_i,\mathcal{D}_j)$, achieving state-of-the-art performance especially when target components share similar data structures.