Continuous-variable Quantum Diffusion Model for State Generation and Restoration

The generation and preservation of complex quantum states against environmental noise are paramount challenges in advancing continuous-variable (CV) quantum information processing. This paper introduces a novel framework based on continuous-variable quantum diffusion principles, synergizing them with CV quantum neural networks (CVQNNs) to address these dual challenges. For the task of state generation, our Continuous-Variable Quantum Diffusion Generative model (CVQD-G) employs a physically driven forward diffusion process using a thermal loss channel, which is then inverted by a learnable, parameter-efficient backward denoising process based on a CVQNN with time-embedding. This framework's capability is further extended for state recovery by the Continuous-Variable Quantum Diffusion Restoration model (CVQD-R), a specialized variant designed to restore quantum states, particularly coherent states with unknown parameters, from thermal degradation. Extensive numerical simulations validate these dual capabilities, demonstrating the high-fidelity generation of diverse Gaussian (coherent, squeezed) and non-Gaussian (Fock, cat) states, typically with fidelities exceeding 99%, and confirming the model's ability to robustly restore corrupted states. Furthermore, a comprehensive complexity analysis reveals favorable training and inference costs, highlighting the framework's efficiency, scalability, and its potential as a robust tool for quantum state engineering and noise mitigation in realistic CV quantum systems.

Quantum Complex-Valued Self-Attention Model

The self-attention mechanism has revolutionized classical machine learning, yet its quantum counterpart remains underexplored in fully harnessing the representational power of quantum states. Current quantum self-attention models exhibit a critical limitation by neglecting the indispensable phase information inherent in quantum systems when compressing attention weights into real-valued overlaps. To address this fundamental gap, we propose the Quantum Complex-Valued Self-Attention Model (QCSAM), the first framework that explicitly leverages complex-valued similarities between quantum states to capture both amplitude and phase relationships. Simultaneously, we enhance the standard Linear Combination of Unitaries (LCUs) method by introducing a Complex LCUs (CLCUs) framework that natively supports complex-valued coefficients. This framework enables the weighting of corresponding quantum values using fixed quantum complex self-attention weights, while also supporting trainable complex-valued parameters for value aggregation and quantum multi-head attention. Experimental evaluations on MNIST and Fashion-MNIST demonstrate our model's superiority over recent quantum self-attention architectures including QKSAN, QSAN, and GQHAN, with multi-head configurations showing consistent advantages over single-head variants. We systematically evaluate model scalability through qubit configurations ranging from 3 to 8 qubits and multi-class classification tasks spanning 2 to 4 categories. Through comprehensive ablation studies, we establish the critical advantage of complex-valued quantum attention weights over real-valued alternatives.

High-efficient Bloch simulation of magnetic resonance imaging sequences based on deep learning

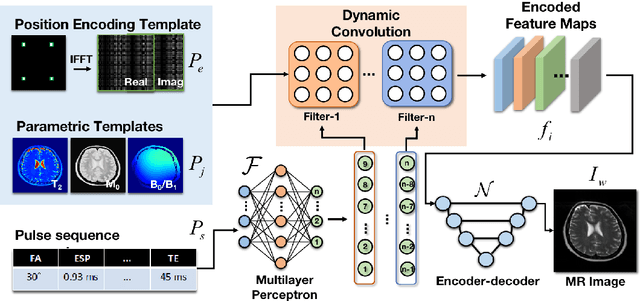
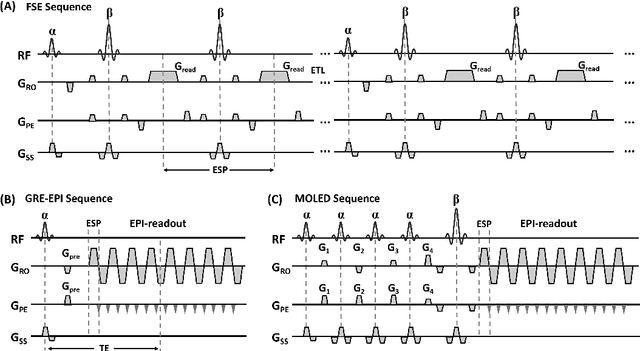
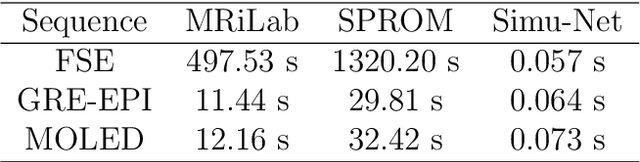
Bloch simulation constitutes an essential part of magnetic resonance imaging (MRI) development. However, even with the graphics processing units (GPU) acceleration, the heavy computational load remains a major challenge, especially in large-scale, high-accuracy simulation scenarios. Here we present a framework based on convolutional neural networks to build a high-efficient 2D Bloch simulator, termed Simu-Net. Compared to the mainstream GPU-based MRI simulation software, Simu-Net successfully accelerates simulations by over hundreds of times in three MRI pulse sequences. The accuracy and robustness of the proposed framework were also verified qualitatively and quantitatively. The trained Simu-Net was applied to generate sufficient customized training samples for deep learning-based T2 mapping and comparable results to conventional methods were obtained in the human brain. As a proof-of-concept work, Simu-Net shows the potential to apply deep learning for rapidly approximating the Bloch equation as a forward physical process.