SWIFT: Scalable Wasserstein Factorization for Sparse Nonnegative Tensors

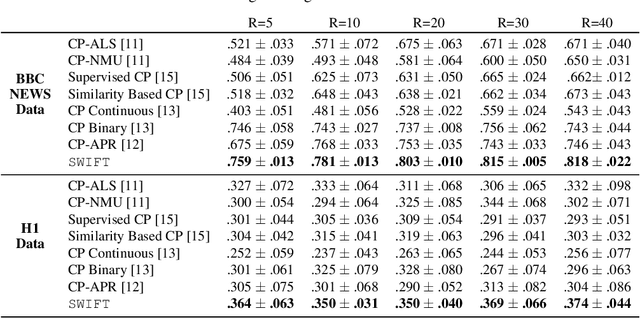
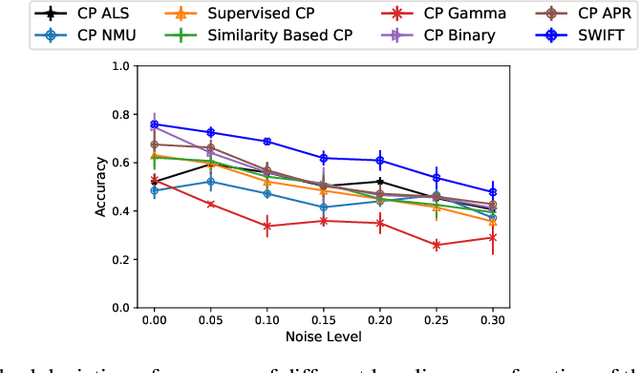
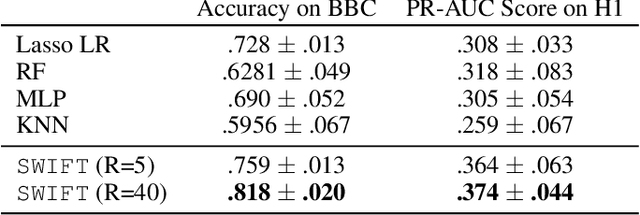
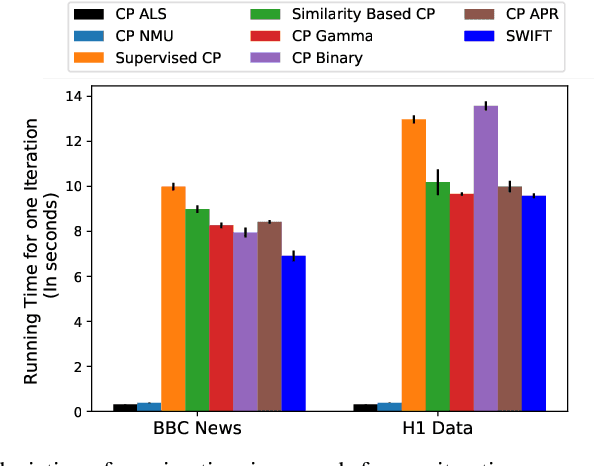
Existing tensor factorization methods assume that the input tensor follows some specific distribution (i.e. Poisson, Bernoulli and Gaussian), and solve the factorization by minimizing some empirical loss functions defined based on the corresponding distribution. However, it suffers from several drawbacks: 1) In reality, the underlying distributions are complicated and unknown, making it infeasible to be approximated by a simple distribution. 2) The correlation across dimensions of the input tensor is not well utilized, leading to sub-optimal performance. Although heuristics were proposed to incorporate such correlation as side information under Gaussian distribution, they can not easily be generalized to other distributions. Thus, a more principled way of utilizing the correlation in tensor factorization models is still an open challenge. Without assuming any explicit distribution, we formulate the tensor factorization as an optimal transport problem with Wasserstein distance, which can handle non-negative inputs. We introduce SWIFT, which minimizes the Wasserstein distance that measures the distance between the input tensor and that of the reconstruction. In particular, we define the N-th order tensor Wasserstein loss for the widely used tensor CP factorization, and derive the optimization algorithm that minimizes it. By leveraging sparsity structure and different equivalent formulations for optimizing computational efficiency, SWIFT is as scalable as other well-known CP algorithms. Using the factor matrices as features, SWIFT achieves up to 9.65% and 11.31% relative improvement over baselines for downstream prediction tasks. Under the noisy conditions, SWIFT achieves up to 15% and 17% relative improvements over the best competitors for the prediction tasks.

TASTE: Temporal and Static Tensor Factorization for Phenotyping Electronic Health Records

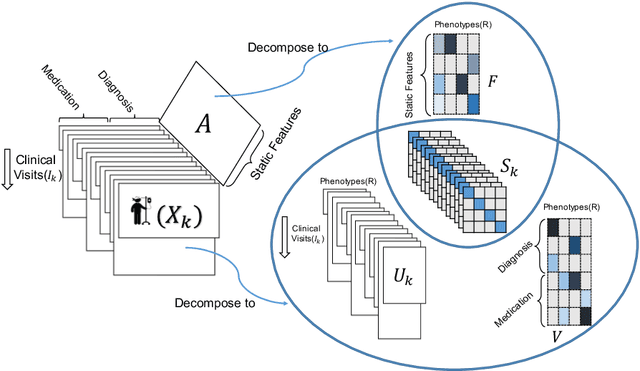
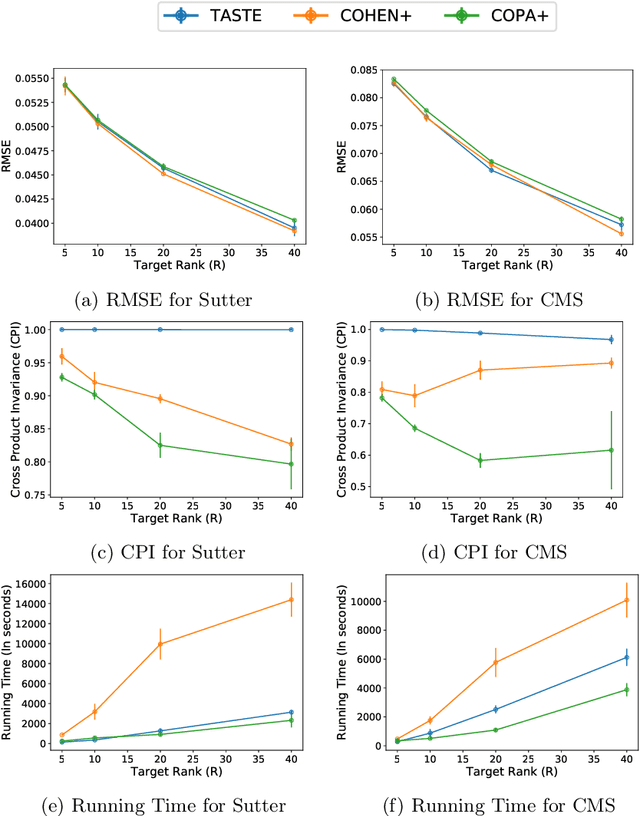
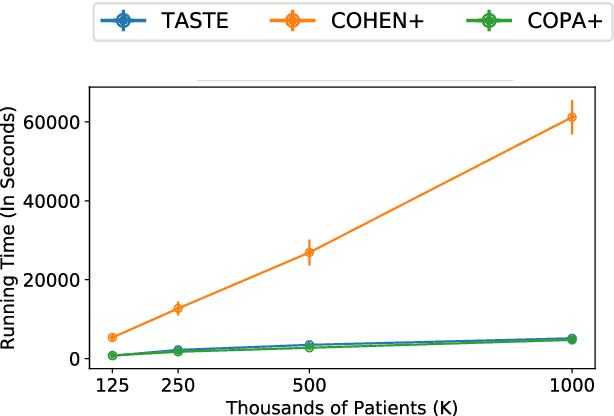
Phenotyping electronic health records (EHR) focuses on defining meaningful patient groups (e.g., heart failure group and diabetes group) and identifying the temporal evolution of patients in those groups. Tensor factorization has been an effective tool for phenotyping. Most of the existing works assume either a static patient representation with aggregate data or only model temporal data. However, real EHR data contain both temporal (e.g., longitudinal clinical visits) and static information (e.g., patient demographics), which are difficult to model simultaneously. In this paper, we propose Temporal And Static TEnsor factorization (TASTE) that jointly models both static and temporal information to extract phenotypes. TASTE combines the PARAFAC2 model with non-negative matrix factorization to model a temporal and a static tensor. To fit the proposed model, we transform the original problem into simpler ones which are optimally solved in an alternating fashion. For each of the sub-problems, our proposed mathematical reformulations lead to efficient sub-problem solvers. Comprehensive experiments on large EHR data from a heart failure (HF) study confirmed that TASTE is up to 14x faster than several baselines and the resulting phenotypes were confirmed to be clinically meaningful by a cardiologist. Using 80 phenotypes extracted by TASTE, a simple logistic regression can achieve the same level of area under the curve (AUC) for HF prediction compared to a deep learning model using recurrent neural networks (RNN) with 345 features.

COPA: Constrained PARAFAC2 for Sparse & Large Datasets

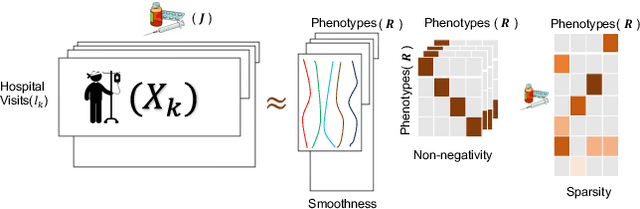
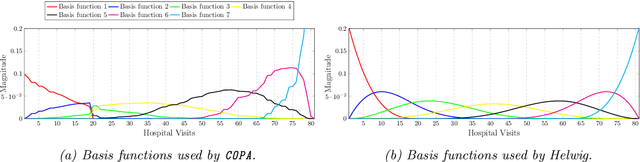
PARAFAC2 has demonstrated success in modeling irregular tensors, where the tensor dimensions vary across one of the modes. An example scenario is modeling treatments across a set of patients with the varying number of medical encounters over time. Despite recent improvements on unconstrained PARAFAC2, its model factors are usually dense and sensitive to noise which limits their interpretability. As a result, the following open challenges remain: a) various modeling constraints, such as temporal smoothness, sparsity and non-negativity, are needed to be imposed for interpretable temporal modeling and b) a scalable approach is required to support those constraints efficiently for large datasets. To tackle these challenges, we propose a {\it CO}nstrained {\it PA}RAFAC2 (COPA) method, which carefully incorporates optimization constraints such as temporal smoothness, sparsity, and non-negativity in the resulting factors. To efficiently support all those constraints, COPA adopts a hybrid optimization framework using alternating optimization and alternating direction method of multiplier (AO-ADMM). As evaluated on large electronic health record (EHR) datasets with hundreds of thousands of patients, COPA achieves significant speedups (up to 36 times faster) over prior PARAFAC2 approaches that only attempt to handle a subset of the constraints that COPA enables. Overall, our method outperforms all the baselines attempting to handle a subset of the constraints in terms of speed, while achieving the same level of accuracy. Through a case study on temporal phenotyping of medically complex children, we demonstrate how the constraints imposed by COPA reveal concise phenotypes and meaningful temporal profiles of patients. The clinical interpretation of both the phenotypes and the temporal profiles was confirmed by a medical expert.