Learning Parametric Distributions from Samples and Preferences

Recent advances in language modeling have underscored the role of preference feedback in enhancing model performance. This paper investigates the conditions under which preference feedback improves parameter estimation in classes of continuous parametric distributions. In our framework, the learner observes pairs of samples from an unknown distribution along with their relative preferences depending on the same unknown parameter. We show that preference-based M-estimators achieve a better asymptotic variance than sample-only M-estimators, further improved by deterministic preferences. Leveraging the hard constraints revealed by deterministic preferences, we propose an estimator achieving an estimation error scaling of $\mathcal{O}(1/n)$ -- a significant improvement over the $\Theta(1/\sqrt{n})$ rate attainable with samples alone. Next, we establish a lower bound that matches this accelerated rate; up to dimension and problem-dependent constants. While the assumptions underpinning our analysis are restrictive, they are satisfied by notable cases such as Gaussian or Laplace distributions for preferences based on the log-probability reward.

Can semi-supervised learning use all the data effectively? A lower bound perspective

Prior works have shown that semi-supervised learning algorithms can leverage unlabeled data to improve over the labeled sample complexity of supervised learning (SL) algorithms. However, existing theoretical analyses focus on regimes where the unlabeled data is sufficient to learn a good decision boundary using unsupervised learning (UL) alone. This begs the question: Can SSL algorithms simultaneously improve upon both UL and SL? To this end, we derive a tight lower bound for 2-Gaussian mixture models that explicitly depends on the labeled and the unlabeled dataset size as well as the signal-to-noise ratio of the mixture distribution. Surprisingly, our result implies that no SSL algorithm can improve upon the minimax-optimal statistical error rates of SL or UL algorithms for these distributions. Nevertheless, we show empirically on real-world data that SSL algorithms can still outperform UL and SL methods. Therefore, our work suggests that, while proving performance gains for SSL algorithms is possible, it requires careful tracking of constants.

A Structured Dictionary Perspective on Implicit Neural Representations

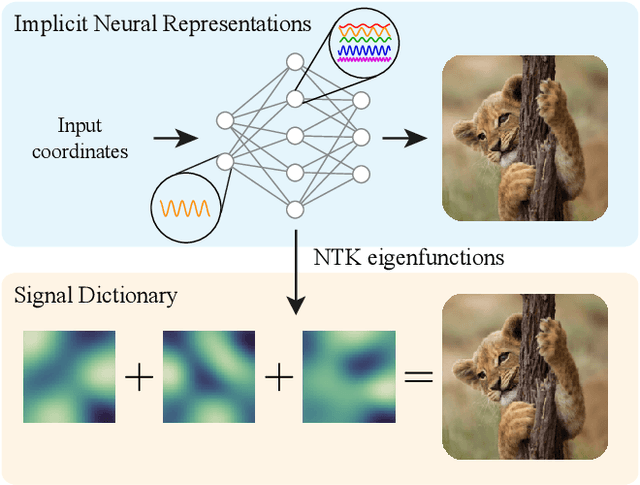
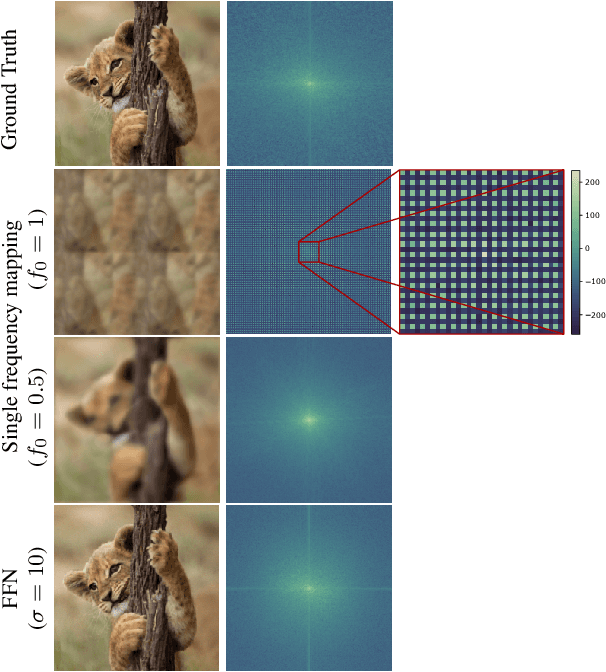
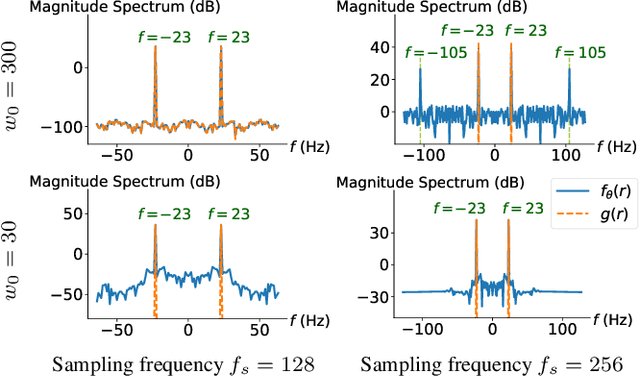
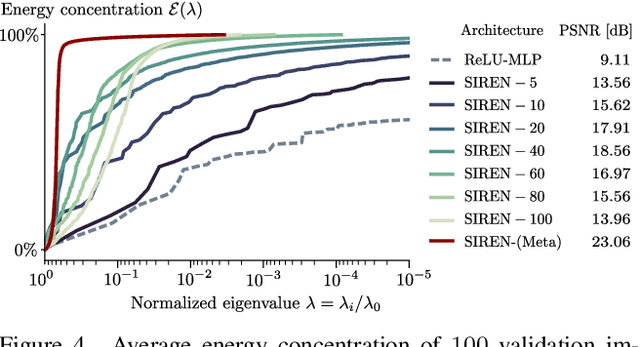
Propelled by new designs that permit to circumvent the spectral bias, implicit neural representations (INRs) have recently emerged as a promising alternative to classical discretized representations of signals. Nevertheless, despite their practical success, we still lack a proper theoretical characterization of how INRs represent signals. In this work, we aim to fill this gap, and we propose a novel unified perspective to theoretically analyse INRs. Leveraging results from harmonic analysis and deep learning theory, we show that most INR families are analogous to structured signal dictionaries whose atoms are integer harmonics of the set of initial mapping frequencies. This structure allows INRs to express signals with an exponentially increasing frequency support using a number of parameters that only grows linearly with depth. Afterwards, we explore the inductive bias of INRs exploiting recent results about the empirical neural tangent kernel (NTK). Specifically, we show that the eigenfunctions of the NTK can be seen as dictionary atoms whose inner product with the target signal determines the final performance of their reconstruction. In this regard, we reveal that meta-learning the initialization has a reshaping effect of the NTK analogous to dictionary learning, building dictionary atoms as a combination of the examples seen during meta-training. Our results permit to design and tune novel INR architectures, but can also be of interest for the wider deep learning theory community.