READER: Reasoning-Enhanced AI-Generated Text Detection

Recent advances in large language models (LLMs) have made it increasingly difficult to distinguish human-written text from AI-generated content. Many existing detectors train supervised neural classifiers that achieve strong in-distribution performance but are often opaque and can degrade substantially under distribution shift. We present READER, a reasoning-enhanced AI text detector that outputs both a human/AI label and a structured rationale describing the evidence for its decision. A key component of our approach is READ, a curated supervision set of rationales and verdicts. We fine-tune an LLM on READ to build READER, which reasons before detecting at inference time. Despite having only 1.5B parameters, READER consistently outperforms existing detectors as well as prompted, high-capacity LLM baselines (GPT-5.2, Gemini-3-Pro, and DeepSeek-V3.2), which are 100 to 1000 times larger in scale.

BASIS: Batchwise Advantage Estimation from Single-Rollout Information Sharing for LLM Reasoning

Reinforcement learning with verifiable rewards has become a standard recipe for improving the reasoning abilities of large language models. Existing algorithms face a tradeoff between computational efficiency and sample efficiency in value estimation and policy learning. We introduce BASIS, a critic-free post-training algorithm designed to address this tradeoff. At each online training step, BASIS samples only one rollout per prompt, but leverages rich information across prompts in the entire batch to improve value function estimation. Our experiments demonstrate that BASIS reduces MSE in value function estimation by 69% compared to REINFORCE++, a representative single-rollout baseline, and achieves lower MSE with one rollout than group mean estimators with 8 rollouts. This improvement in value estimation translates to better policy optimization: using substantially less training time, BASIS achieves performance close to multi-rollout GRPO-type baselines and often outperforms single-rollout REINFORCE-type baselines.

Statistical Guarantees for Reasoning Probes on Looped Boolean Circuits

We study the statistical behaviour of reasoning probes in a stylized model of looped reasoning, given by Boolean circuits whose computational graph is a perfect $ν$-ary tree ($ν\ge 2$) and whose output is appended to the input and fed back iteratively for subsequent computation rounds. A reasoning probe has access to a sampled subset of internal computation nodes, possibly without covering the entire graph, and seeks to infer which $ν$-ary Boolean gate is executed at each queried node, representing uncertainty via a probability distribution over a fixed collection of $\mathtt{m}$ admissible $ν$-ary gates. This partial observability induces a generalization problem, which we analyze in a realizable, transductive setting. We show that, when the reasoning probe is parameterized by a graph convolutional network (GCN)-based hypothesis class and queries $N$ nodes, the worst-case generalization error attains the optimal rate $\mathcal{O}(\sqrt{\log(2/δ)}/\sqrt{N})$ with probability at least $1-δ$, for $δ\in (0,1)$. Our analysis combines snowflake metric embedding techniques with tools from statistical optimal transport. A key insight is that this optimal rate is achievable independently of graph size, owing to the existence of a low-distortion one-dimensional snowflake embedding of the induced graph metric. As a consequence, our results provide a sharp characterization of how structural properties of the computational graph govern the statistical efficiency of reasoning under partial access.

Learning from one graph: transductive learning guarantees via the geometry of small random worlds

Since their introduction by Kipf and Welling in $2017$, a primary use of graph convolutional networks is transductive node classification, where missing labels are inferred within a single observed graph and its feature matrix. Despite the widespread use of the network model, the statistical foundations of transductive learning remain limited, as standard inference frameworks typically rely on multiple independent samples rather than a single graph. In this work, we address these gaps by developing new concentration-of-measure tools that leverage the geometric regularities of large graphs via low-dimensional metric embeddings. The emergent regularities are captured using a random graph model; however, the methods remain applicable to deterministic graphs once observed. We establish two principal learning results. The first concerns arbitrary deterministic $k$-vertex graphs, and the second addresses random graphs that share key geometric properties with an Erd\H{o}s-R\'{e}nyi graph $\mathbf{G}=\mathbf{G}(k,p)$ in the regime $p \in \mathcal{O}((\log (k)/k)^{1/2})$. The first result serves as the basis for and illuminates the second. We then extend these results to the graph convolutional network setting, where additional challenges arise. Lastly, our learning guarantees remain informative even with a few labelled nodes $N$ and achieve the optimal nonparametric rate $\mathcal{O}(N^{-1/2})$ as $N$ grows.

Low-dimensional approximations of the conditional law of Volterra processes: a non-positive curvature approach

Predicting the conditional evolution of Volterra processes with stochastic volatility is a crucial challenge in mathematical finance. While deep neural network models offer promise in approximating the conditional law of such processes, their effectiveness is hindered by the curse of dimensionality caused by the infinite dimensionality and non-smooth nature of these problems. To address this, we propose a two-step solution. Firstly, we develop a stable dimension reduction technique, projecting the law of a reasonably broad class of Volterra process onto a low-dimensional statistical manifold of non-positive sectional curvature. Next, we introduce a sequentially deep learning model tailored to the manifold's geometry, which we show can approximate the projected conditional law of the Volterra process. Our model leverages an auxiliary hypernetwork to dynamically update its internal parameters, allowing it to encode non-stationary dynamics of the Volterra process, and it can be interpreted as a gating mechanism in a mixture of expert models where each expert is specialized at a specific point in time. Our hypernetwork further allows us to achieve approximation rates that would seemingly only be possible with very large networks.

Designing Universal Causal Deep Learning Models: The Case of Infinite-Dimensional Dynamical Systems from Stochastic Analysis

Deep learning (DL) is becoming indispensable to contemporary stochastic analysis and finance; nevertheless, it is still unclear how to design a principled DL framework for approximating infinite-dimensional causal operators. This paper proposes a "geometry-aware" solution to this open problem by introducing a DL model-design framework that takes a suitable infinite-dimensional linear metric spaces as inputs and returns a universal sequential DL models adapted to these linear geometries: we call these models Causal Neural Operators (CNO). Our main result states that the models produced by our framework can uniformly approximate on compact sets and across arbitrarily finite-time horizons H\"older or smooth trace class operators which causally map sequences between given linear metric spaces. Consequentially, we deduce that a single CNO can efficiently approximate the solution operator to a broad range of SDEs, thus allowing us to simultaneously approximate predictions from families of SDE models, which is vital to computational robust finance. We deduce that the CNO can approximate the solution operator to most stochastic filtering problems, implying that a single CNO can simultaneously filter a family of partially observed stochastic volatility models.

One-Shot Learning of Stochastic Differential Equations with Computational Graph Completion

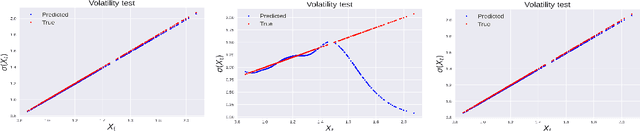
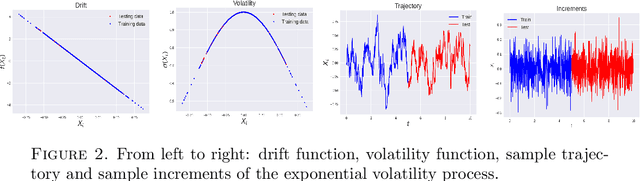
We consider the problem of learning Stochastic Differential Equations of the form $dX_t = f(X_t)dt+\sigma(X_t)dW_t $ from one sample trajectory. This problem is more challenging than learning deterministic dynamical systems because one sample trajectory only provides indirect information on the unknown functions $f$, $\sigma$, and stochastic process $dW_t$ representing the drift, the diffusion, and the stochastic forcing terms, respectively. We propose a simple kernel-based solution to this problem that can be decomposed as follows: (1) Represent the time-increment map $X_t \rightarrow X_{t+dt}$ as a Computational Graph in which $f$, $\sigma$ and $dW_t$ appear as unknown functions and random variables. (2) Complete the graph (approximate unknown functions and random variables) via Maximum a Posteriori Estimation (given the data) with Gaussian Process (GP) priors on the unknown functions. (3) Learn the covariance functions (kernels) of the GP priors from data with randomized cross-validation. Numerical experiments illustrate the efficacy, robustness, and scope of our method.