Spectral bias in physics-informed and operator learning: Analysis and mitigation guidelines

Solving partial differential equations (PDEs) by neural networks as well as Kolmogorov-Arnold Networks (KANs), including physics-informed neural networks (PINNs), physics-informed KANs (PIKANs), and neural operators, are known to exhibit spectral bias, whereby low-frequency components of the solution are learned significantly faster than high-frequency modes. While spectral bias is often treated as an intrinsic representational limitation of neural architectures, its interaction with optimization dynamics and physics-based loss formulations remains poorly understood. In this work, we provide a systematic investigation of spectral bias in physics-informed and operator learning frameworks, with emphasis on the coupled roles of network architecture, activation functions, loss design, and optimization strategy. We quantify spectral bias through frequency-resolved error metrics, Barron-norm diagnostics, and higher-order statistical moments, enabling a unified analysis across elliptic, hyperbolic, and dispersive PDEs. Through diverse benchmark problems, including the Korteweg-de Vries, wave and steady-state diffusion-reaction equations, turbulent flow reconstruction, and earthquake dynamics, we demonstrate that spectral bias is not simply representational but fundamentally dynamical. In particular, second-order optimization methods substantially alter the spectral learning order, enabling earlier and more accurate recovery of high-frequency modes for all PDE types. For neural operators, we further show that spectral bias is dependent on the neural operator architecture and can also be effectively mitigated through spectral-aware loss formulations without increasing the inference cost.

EventFlow: Real-Time Neuromorphic Event-Driven Classification of Two-Phase Boiling Flow Regimes

Flow boiling is an efficient heat transfer mechanism capable of dissipating high heat loads with minimal temperature variation, making it an ideal thermal management method. However, sudden shifts between flow regimes can disrupt thermal performance and system reliability, highlighting the need for accurate and low-latency real-time monitoring. Conventional optical imaging methods are limited by high computational demands and insufficient temporal resolution, making them inadequate for capturing transient flow behavior. To address this, we propose a real-time framework based on signals from neuromorphic sensors for flow regime classification. Neuromorphic sensors detect changes in brightness at individual pixels, which typically correspond to motion at edges, enabling fast and efficient detection without full-frame reconstruction, providing event-based information. We develop five classification models using both traditional image data and event-based data, demonstrating that models leveraging event data outperform frame-based approaches due to their sensitivity to dynamic flow features. Among these models, the event-based long short-term memory model provides the best balance between accuracy and speed, achieving 97.6% classification accuracy with a processing time of 0.28 ms. Our asynchronous processing pipeline supports continuous, low-latency predictions and delivers stable output through a majority voting mechanisms, enabling reliable real-time feedback for experimental control and intelligent thermal management.

Learning Turbulent Flows with Generative Models: Super-resolution, Forecasting, and Sparse Flow Reconstruction

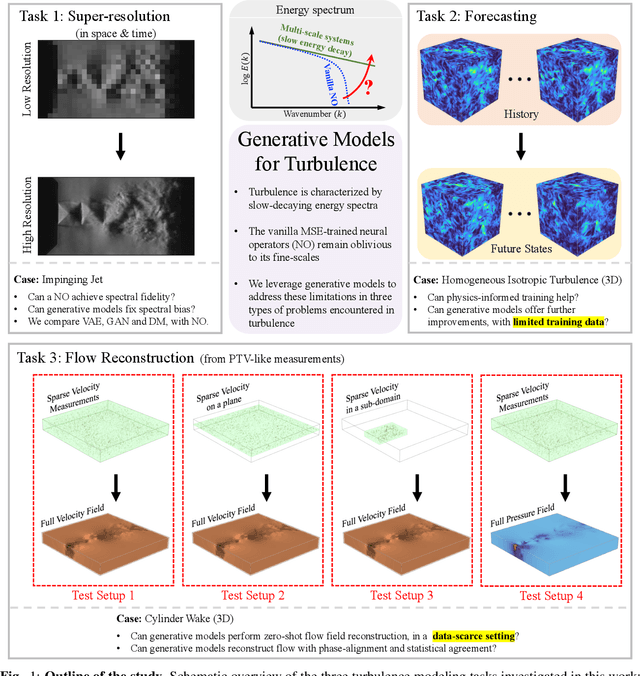
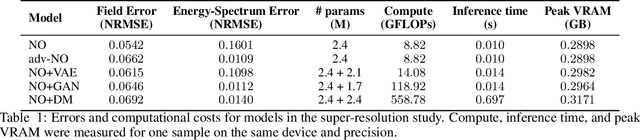
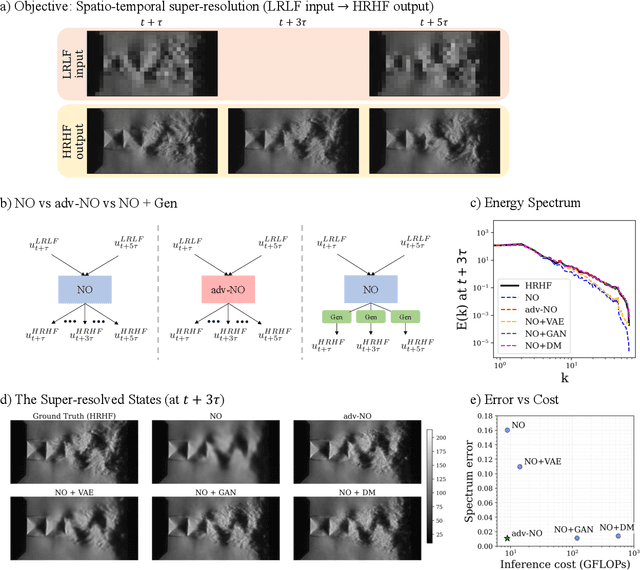
Neural operators are promising surrogates for dynamical systems but when trained with standard L2 losses they tend to oversmooth fine-scale turbulent structures. Here, we show that combining operator learning with generative modeling overcomes this limitation. We consider three practical turbulent-flow challenges where conventional neural operators fail: spatio-temporal super-resolution, forecasting, and sparse flow reconstruction. For Schlieren jet super-resolution, an adversarially trained neural operator (adv-NO) reduces the energy-spectrum error by 15x while preserving sharp gradients at neural operator-like inference cost. For 3D homogeneous isotropic turbulence, adv-NO trained on only 160 timesteps from a single trajectory forecasts accurately for five eddy-turnover times and offers 114x wall-clock speed-up at inference than the baseline diffusion-based forecasters, enabling near-real-time rollouts. For reconstructing cylinder wake flows from highly sparse Particle Tracking Velocimetry-like inputs, a conditional generative model infers full 3D velocity and pressure fields with correct phase alignment and statistics. These advances enable accurate reconstruction and forecasting at low compute cost, bringing near-real-time analysis and control within reach in experimental and computational fluid mechanics. See our project page: https://vivekoommen.github.io/Gen4Turb/

Mitigating Spectral Bias in Neural Operators via High-Frequency Scaling for Physical Systems

Neural operators have emerged as powerful surrogates for modeling complex physical problems. However, they suffer from spectral bias making them oblivious to high-frequency modes, which are present in multiscale physical systems. Therefore, they tend to produce over-smoothed solutions, which is particularly problematic in modeling turbulence and for systems with intricate patterns and sharp gradients such as multi-phase flow systems. In this work, we introduce a new approach named high-frequency scaling (HFS) to mitigate spectral bias in convolutional-based neural operators. By integrating HFS with proper variants of UNet neural operators, we demonstrate a higher prediction accuracy by mitigating spectral bias in single and two-phase flow problems. Unlike Fourier-based techniques, HFS is directly applied to the latent space, thus eliminating the computational cost associated with the Fourier transform. Additionally, we investigate alternative spectral bias mitigation through diffusion models conditioned on neural operators. While the diffusion model integrated with the standard neural operator may still suffer from significant errors, these errors are substantially reduced when the diffusion model is integrated with a HFS-enhanced neural operator.