Dynamic Visualization and Fast Computation for Convex Clustering via Algorithmic Regularization

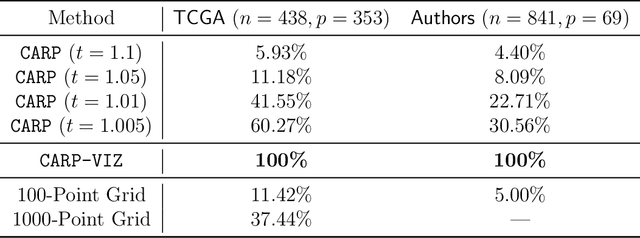
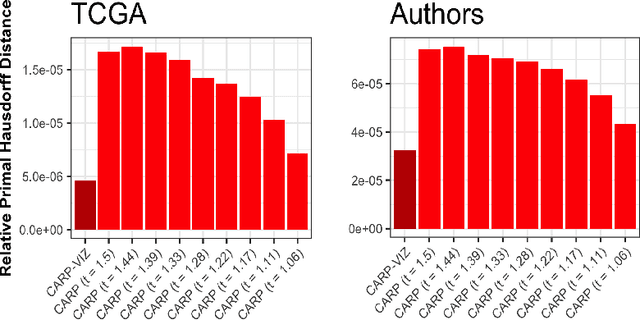
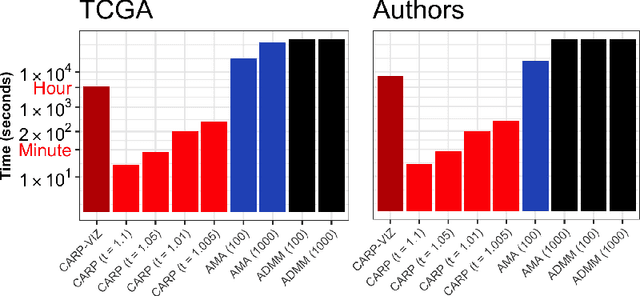
Convex clustering is a promising new approach to the classical problem of clustering, combining strong performance in empirical studies with rigorous theoretical foundations. Despite these advantages, convex clustering has not been widely adopted, due to its computationally intensive nature and its lack of compelling visualizations. To address these impediments, we introduce Algorithmic Regularization, an innovative technique for obtaining high-quality estimates of regularization paths using an iterative one-step approximation scheme. We justify our approach with a novel theoretical result, guaranteeing global convergence of the approximate path to the exact solution under easily-checked non-data-dependent assumptions. The application of algorithmic regularization to convex clustering yields the Convex Clustering via Algorithmic Regularization Paths (CARP) algorithm for computing the clustering solution path. On example data sets from genomics and text analysis, CARP delivers over a 100-fold speed-up over existing methods, while attaining a finer approximation grid than standard methods. Furthermore, CARP enables improved visualization of clustering solutions: the fine solution grid returned by CARP can be used to construct a convex clustering-based dendrogram, as well as forming the basis of a dynamic path-wise visualization based on modern web technologies. Our methods are implemented in the open-source R package clustRviz, available at https://github.com/DataSlingers/clustRviz.

A Review of Multivariate Distributions for Count Data Derived from the Poisson Distribution

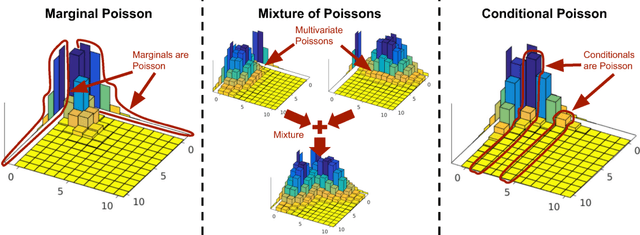
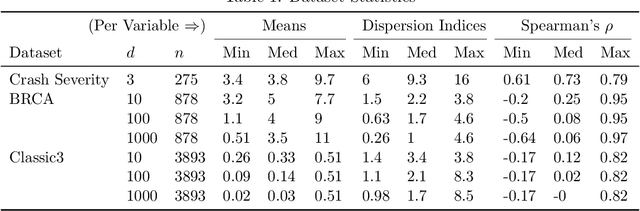
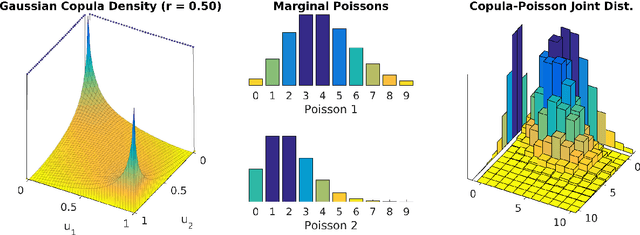
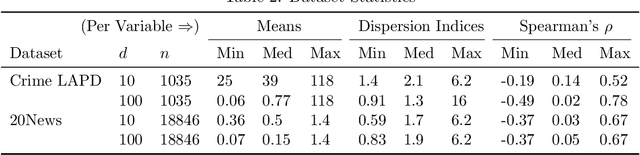
The Poisson distribution has been widely studied and used for modeling univariate count-valued data. Multivariate generalizations of the Poisson distribution that permit dependencies, however, have been far less popular. Yet, real-world high-dimensional count-valued data found in word counts, genomics, and crime statistics, for example, exhibit rich dependencies, and motivate the need for multivariate distributions that can appropriately model this data. We review multivariate distributions derived from the univariate Poisson, categorizing these models into three main classes: 1) where the marginal distributions are Poisson, 2) where the joint distribution is a mixture of independent multivariate Poisson distributions, and 3) where the node-conditional distributions are derived from the Poisson. We discuss the development of multiple instances of these classes and compare the models in terms of interpretability and theory. Then, we empirically compare multiple models from each class on three real-world datasets that have varying data characteristics from different domains, namely traffic accident data, biological next generation sequencing data, and text data. These empirical experiments develop intuition about the comparative advantages and disadvantages of each class of multivariate distribution that was derived from the Poisson. Finally, we suggest new research directions as explored in the subsequent discussion section.

Convex Biclustering

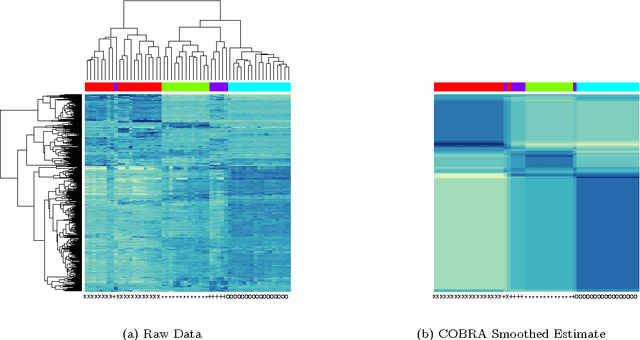
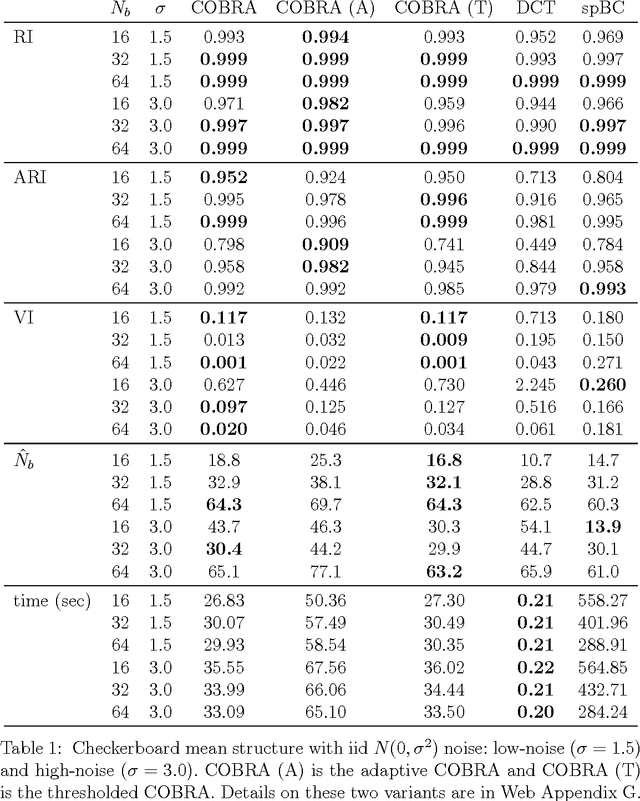
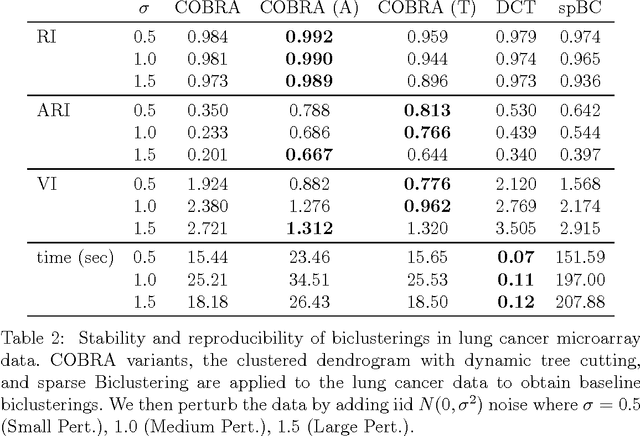
In the biclustering problem, we seek to simultaneously group observations and features. While biclustering has applications in a wide array of domains, ranging from text mining to collaborative filtering, the problem of identifying structure in high dimensional genomic data motivates this work. In this context, biclustering enables us to identify subsets of genes that are co-expressed only within a subset of experimental conditions. We present a convex formulation of the biclustering problem that possesses a unique global minimizer and an iterative algorithm, COBRA, that is guaranteed to identify it. Our approach generates an entire solution path of possible biclusters as a single tuning parameter is varied. We also show how to reduce the problem of selecting this tuning parameter to solving a trivial modification of the convex biclustering problem. The key contributions of our work are its simplicity, interpretability, and algorithmic guarantees - features that arguably are lacking in the current alternative algorithms. We demonstrate the advantages of our approach, which includes stably and reproducibly identifying biclusterings, on simulated and real microarray data.

On Graphical Models via Univariate Exponential Family Distributions

Undirected graphical models, or Markov networks, are a popular class of statistical models, used in a wide variety of applications. Popular instances of this class include Gaussian graphical models and Ising models. In many settings, however, it might not be clear which subclass of graphical models to use, particularly for non-Gaussian and non-categorical data. In this paper, we consider a general sub-class of graphical models where the node-wise conditional distributions arise from exponential families. This allows us to derive multivariate graphical model distributions from univariate exponential family distributions, such as the Poisson, negative binomial, and exponential distributions. Our key contributions include a class of M-estimators to fit these graphical model distributions; and rigorous statistical analysis showing that these M-estimators recover the true graphical model structure exactly, with high probability. We provide examples of genomic and proteomic networks learned via instances of our class of graphical models derived from Poisson and exponential distributions.

A General Framework for Mixed Graphical Models

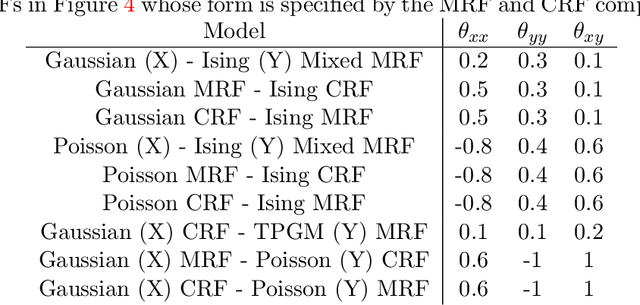
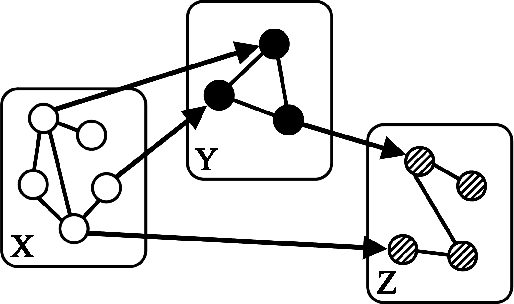
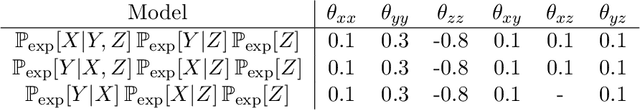
"Mixed Data" comprising a large number of heterogeneous variables (e.g. count, binary, continuous, skewed continuous, among other data types) are prevalent in varied areas such as genomics and proteomics, imaging genetics, national security, social networking, and Internet advertising. There have been limited efforts at statistically modeling such mixed data jointly, in part because of the lack of computationally amenable multivariate distributions that can capture direct dependencies between such mixed variables of different types. In this paper, we address this by introducing a novel class of Block Directed Markov Random Fields (BDMRFs). Using the basic building block of node-conditional univariate exponential families from Yang et al. (2012), we introduce a class of mixed conditional random field distributions, that are then chained according to a block-directed acyclic graph to form our class of Block Directed Markov Random Fields (BDMRFs). The Markov independence graph structure underlying a BDMRF thus has both directed and undirected edges. We introduce conditions under which these distributions exist and are normalizable, study several instances of our models, and propose scalable penalized conditional likelihood estimators with statistical guarantees for recovering the underlying network structure. Simulations as well as an application to learning mixed genomic networks from next generation sequencing expression data and mutation data demonstrate the versatility of our methods.

Sparse and Functional Principal Components Analysis

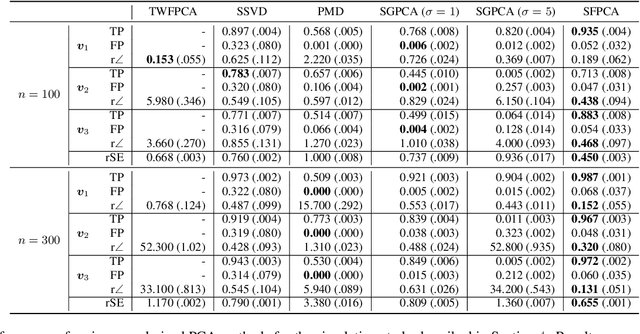
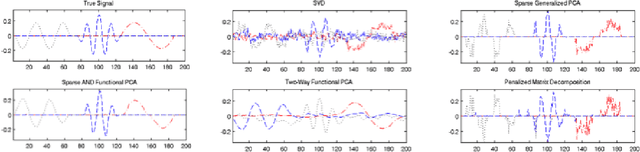
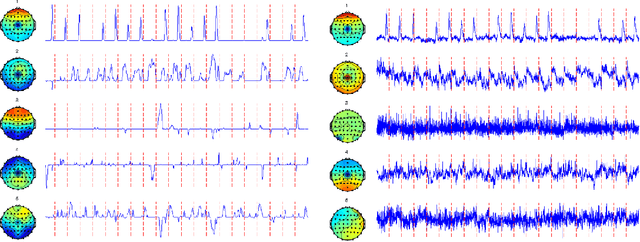
Regularized principal components analysis, especially Sparse PCA and Functional PCA, has become widely used for dimension reduction in high-dimensional settings. Many examples of massive data, however, may benefit from estimating both sparse AND functional factors. These include neuroimaging data where there are discrete brain regions of activation (sparsity) but these regions tend to be smooth spatially (functional). Here, we introduce an optimization framework that can encourage both sparsity and smoothness of the row and/or column PCA factors. This framework generalizes many of the existing approaches to Sparse PCA, Functional PCA and two-way Sparse PCA and Functional PCA, as these are all special cases of our method. In particular, our method permits flexible combinations of sparsity and smoothness that lead to improvements in feature selection and signal recovery as well as more interpretable PCA factors. We demonstrate our method on simulated data and a neuroimaging example on EEG data. This work provides a unified framework for regularized PCA that can form the foundation for a cohesive approach to regularization in high-dimensional multivariate analysis.

Regularized Partial Least Squares with an Application to NMR Spectroscopy

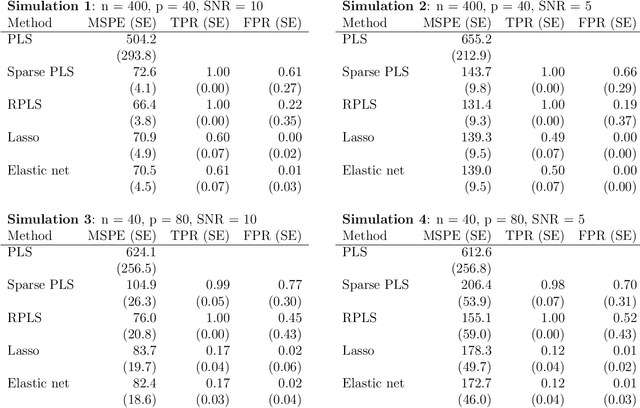
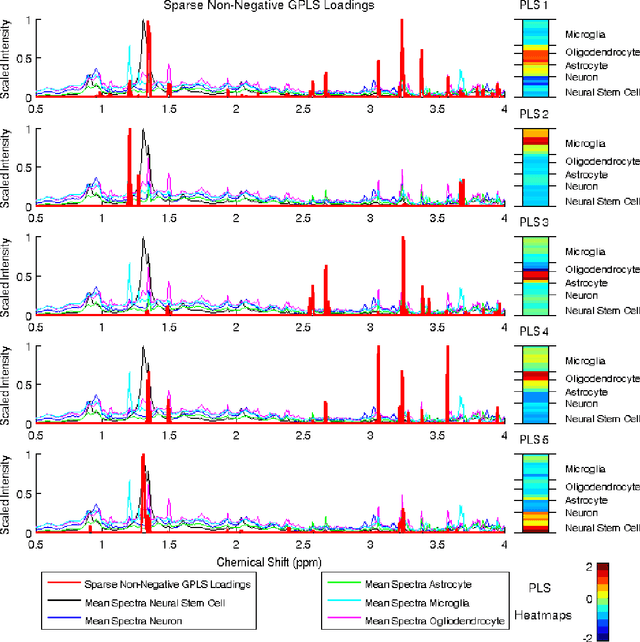
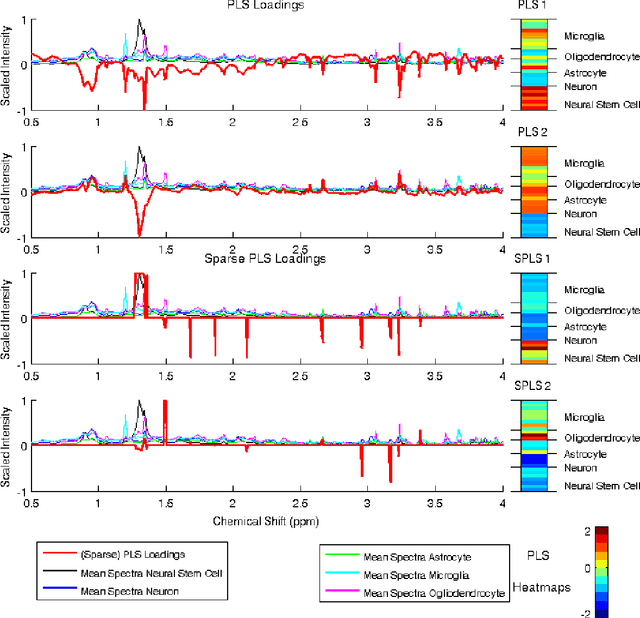
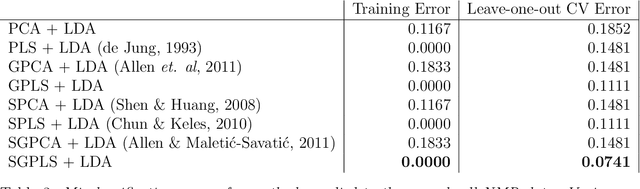
High-dimensional data common in genomics, proteomics, and chemometrics often contains complicated correlation structures. Recently, partial least squares (PLS) and Sparse PLS methods have gained attention in these areas as dimension reduction techniques in the context of supervised data analysis. We introduce a framework for Regularized PLS by solving a relaxation of the SIMPLS optimization problem with penalties on the PLS loadings vectors. Our approach enjoys many advantages including flexibility, general penalties, easy interpretation of results, and fast computation in high-dimensional settings. We also outline extensions of our methods leading to novel methods for Non-negative PLS and Generalized PLS, an adaption of PLS for structured data. We demonstrate the utility of our methods through simulations and a case study on proton Nuclear Magnetic Resonance (NMR) spectroscopy data.

A Generalized Least Squares Matrix Decomposition

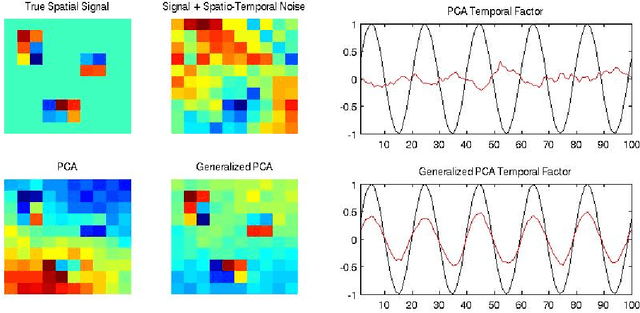
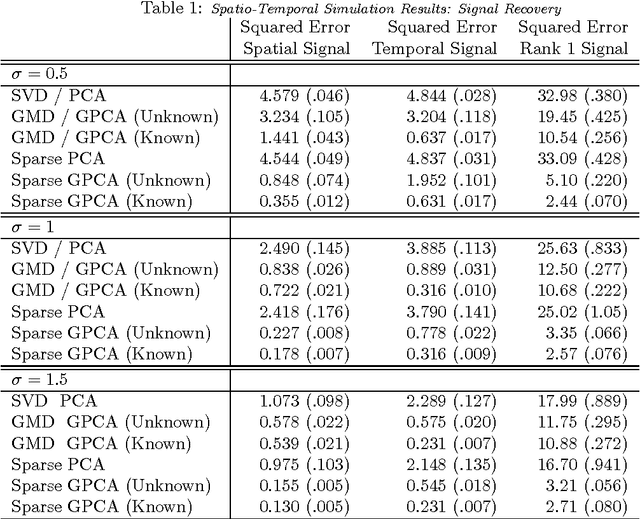
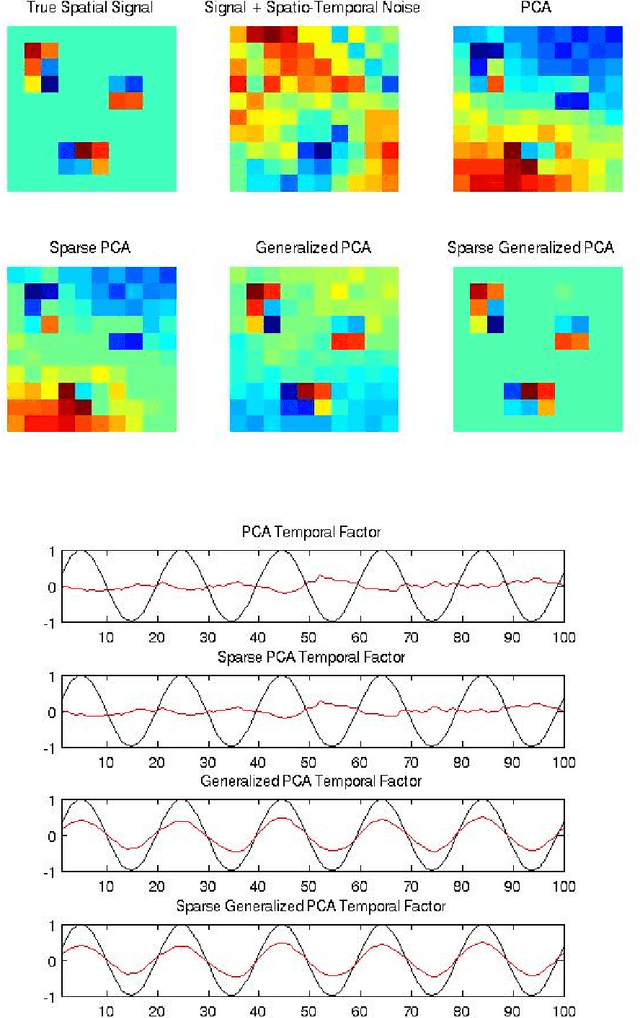
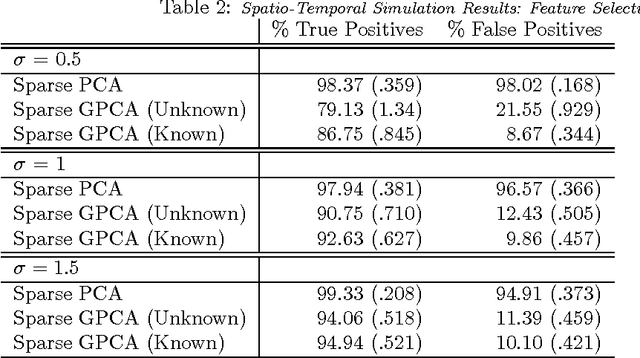
Variables in many massive high-dimensional data sets are structured, arising for example from measurements on a regular grid as in imaging and time series or from spatial-temporal measurements as in climate studies. Classical multivariate techniques ignore these structural relationships often resulting in poor performance. We propose a generalization of the singular value decomposition (SVD) and principal components analysis (PCA) that is appropriate for massive data sets with structured variables or known two-way dependencies. By finding the best low rank approximation of the data with respect to a transposable quadratic norm, our decomposition, entitled the Generalized least squares Matrix Decomposition (GMD), directly accounts for structural relationships. As many variables in high-dimensional settings are often irrelevant or noisy, we also regularize our matrix decomposition by adding two-way penalties to encourage sparsity or smoothness. We develop fast computational algorithms using our methods to perform generalized PCA (GPCA), sparse GPCA, and functional GPCA on massive data sets. Through simulations and a whole brain functional MRI example we demonstrate the utility of our methodology for dimension reduction, signal recovery, and feature selection with high-dimensional structured data.

Regularized Tensor Factorizations and Higher-Order Principal Components Analysis

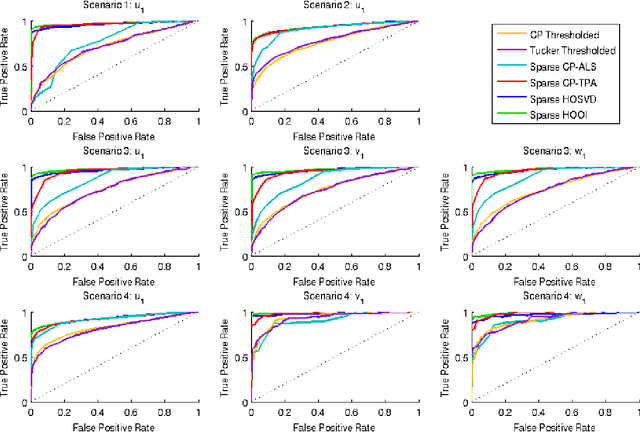
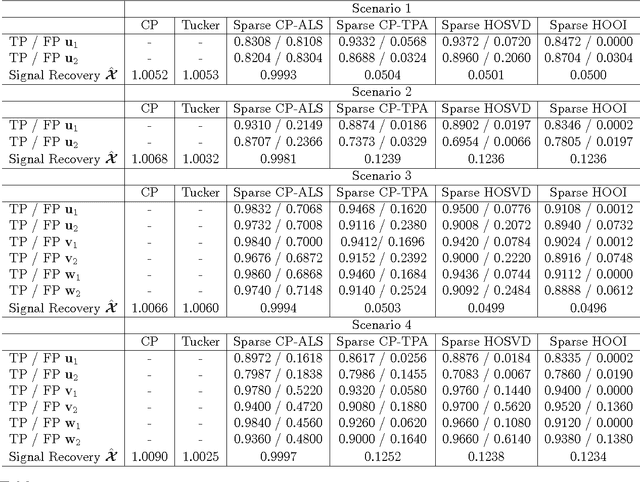
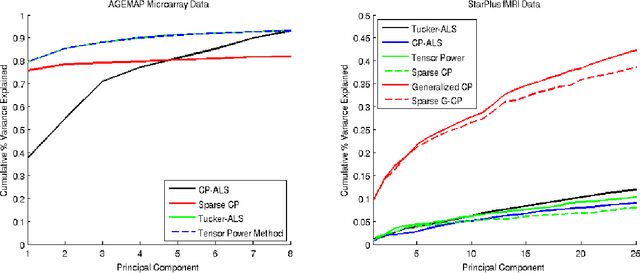
High-dimensional tensors or multi-way data are becoming prevalent in areas such as biomedical imaging, chemometrics, networking and bibliometrics. Traditional approaches to finding lower dimensional representations of tensor data include flattening the data and applying matrix factorizations such as principal components analysis (PCA) or employing tensor decompositions such as the CANDECOMP / PARAFAC (CP) and Tucker decompositions. The former can lose important structure in the data, while the latter Higher-Order PCA (HOPCA) methods can be problematic in high-dimensions with many irrelevant features. We introduce frameworks for sparse tensor factorizations or Sparse HOPCA based on heuristic algorithmic approaches and by solving penalized optimization problems related to the CP decomposition. Extensions of these approaches lead to methods for general regularized tensor factorizations, multi-way Functional HOPCA and generalizations of HOPCA for structured data. We illustrate the utility of our methods for dimension reduction, feature selection, and signal recovery on simulated data and multi-dimensional microarrays and functional MRIs.

Transposable regularized covariance models with an application to missing data imputation

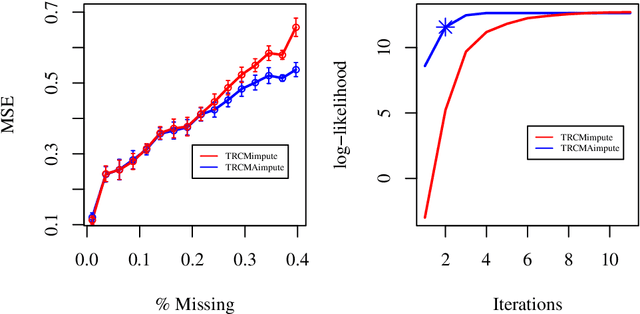
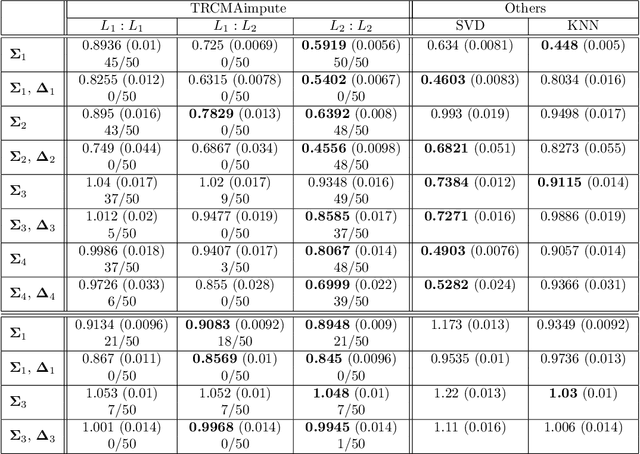
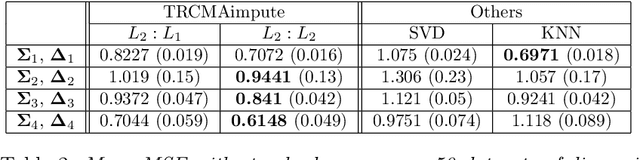
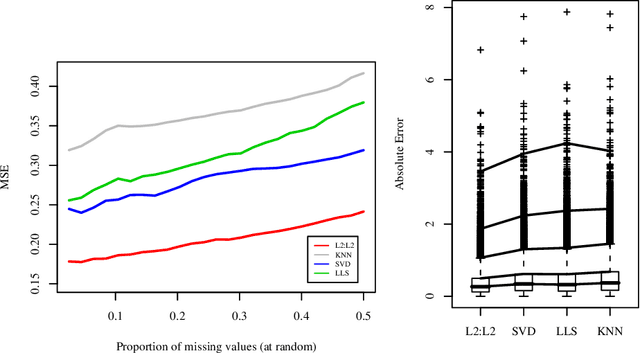
Missing data estimation is an important challenge with high-dimensional data arranged in the form of a matrix. Typically this data matrix is transposable, meaning that either the rows, columns or both can be treated as features. To model transposable data, we present a modification of the matrix-variate normal, the mean-restricted matrix-variate normal, in which the rows and columns each have a separate mean vector and covariance matrix. By placing additive penalties on the inverse covariance matrices of the rows and columns, these so-called transposable regularized covariance models allow for maximum likelihood estimation of the mean and nonsingular covariance matrices. Using these models, we formulate EM-type algorithms for missing data imputation in both the multivariate and transposable frameworks. We present theoretical results exploiting the structure of our transposable models that allow these models and imputation methods to be applied to high-dimensional data. Simulations and results on microarray data and the Netflix data show that these imputation techniques often outperform existing methods and offer a greater degree of flexibility.