Contrastive Diffusion Alignment: Learning Structured Latents for Controllable Generation

Diffusion models excel at generation, but their latent spaces are not explicitly organized for interpretable control. We introduce ConDA (Contrastive Diffusion Alignment), a framework that applies contrastive learning within diffusion embeddings to align latent geometry with system dynamics. Motivated by recent advances showing that contrastive objectives can recover more disentangled and structured representations, ConDA organizes diffusion latents such that traversal directions reflect underlying dynamical factors. Within this contrastively structured space, ConDA enables nonlinear trajectory traversal that supports faithful interpolation, extrapolation, and controllable generation. Across benchmarks in fluid dynamics, neural calcium imaging, therapeutic neurostimulation, and facial expression, ConDA produces interpretable latent representations with improved controllability compared to linear traversals and conditioning-based baselines. These results suggest that diffusion latents encode dynamics-relevant structure, but exploiting this structure requires latent organization and traversal along the latent manifold.

Hierarchically Clustered PCA and CCA via a Convex Clustering Penalty

We introduce an unsupervised learning approach that combines the truncated singular value decomposition with convex clustering to estimate within-cluster directions of maximum variance/covariance (in the variables) while simultaneously hierarchically clustering (on observations). In contrast to previous work on joint clustering and embedding, our approach has a straightforward formulation, is readily scalable via distributed optimization, and admits a direct interpretation as hierarchically clustered principal component analysis (PCA) or hierarchically clustered canonical correlation analysis (CCA). Through numerical experiments and real-world examples relevant to precision medicine, we show that our approach outperforms traditional and contemporary clustering methods on underdetermined problems ($p \gg N$ with tens of observations) and scales to large datasets (e.g., $N=100,000$; $p=1,000$) while yielding interpretable dendrograms of hierarchical per-cluster principal components or canonical variates.

A Generalized Least Squares Matrix Decomposition

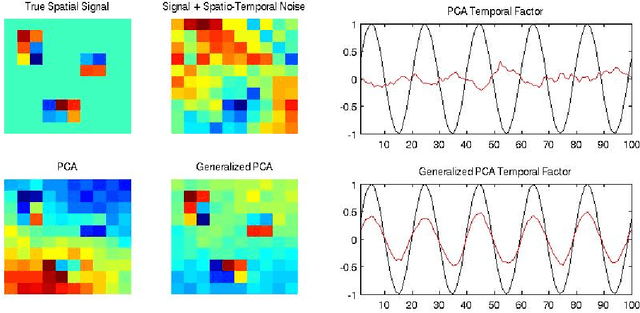
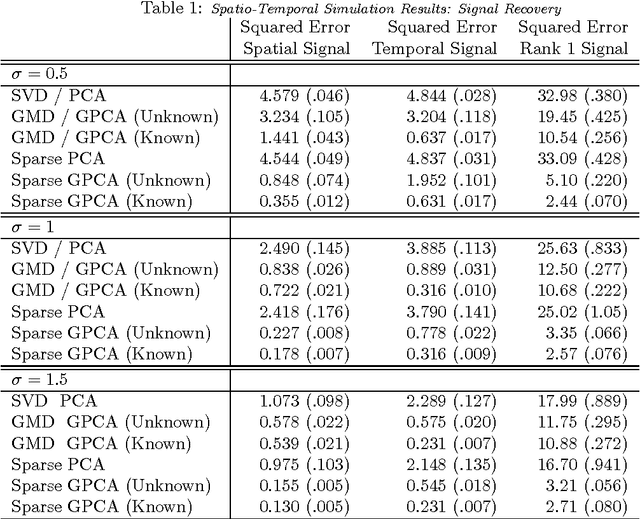
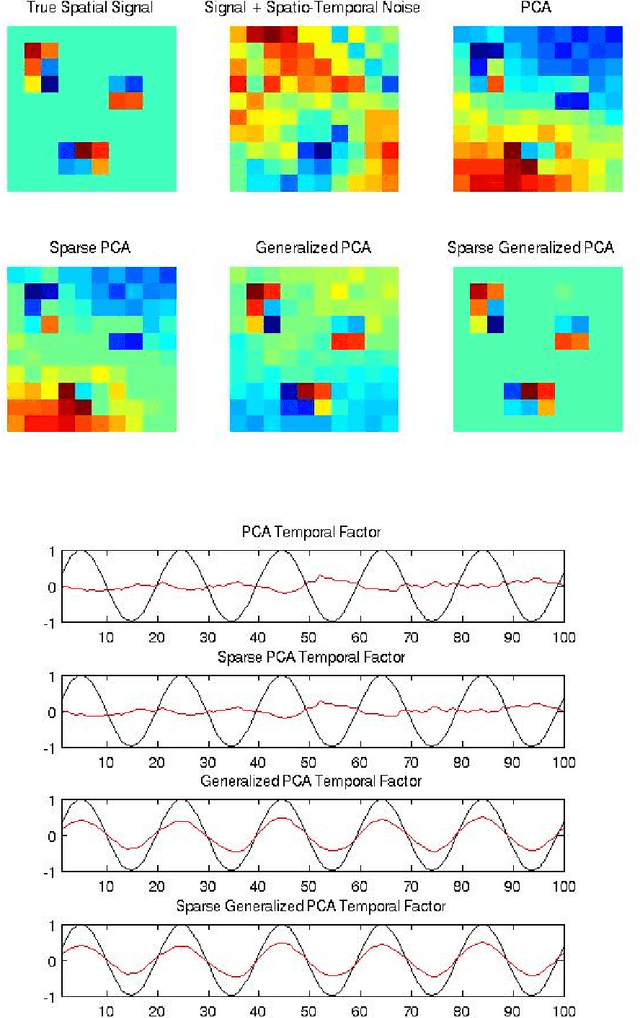
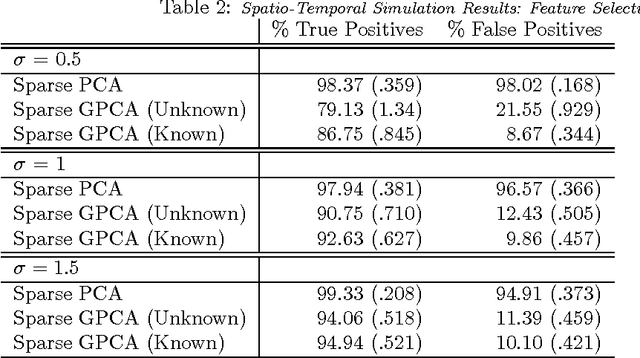
Variables in many massive high-dimensional data sets are structured, arising for example from measurements on a regular grid as in imaging and time series or from spatial-temporal measurements as in climate studies. Classical multivariate techniques ignore these structural relationships often resulting in poor performance. We propose a generalization of the singular value decomposition (SVD) and principal components analysis (PCA) that is appropriate for massive data sets with structured variables or known two-way dependencies. By finding the best low rank approximation of the data with respect to a transposable quadratic norm, our decomposition, entitled the Generalized least squares Matrix Decomposition (GMD), directly accounts for structural relationships. As many variables in high-dimensional settings are often irrelevant or noisy, we also regularize our matrix decomposition by adding two-way penalties to encourage sparsity or smoothness. We develop fast computational algorithms using our methods to perform generalized PCA (GPCA), sparse GPCA, and functional GPCA on massive data sets. Through simulations and a whole brain functional MRI example we demonstrate the utility of our methodology for dimension reduction, signal recovery, and feature selection with high-dimensional structured data.