Understanding InfoNCE: Transition Probability Matrix Induced Feature Clustering

Contrastive learning has emerged as a cornerstone of unsupervised representation learning across vision, language, and graph domains, with InfoNCE as its dominant objective. Despite its empirical success, the theoretical underpinnings of InfoNCE remain limited. In this work, we introduce an explicit feature space to model augmented views of samples and a transition probability matrix to capture data augmentation dynamics. We demonstrate that InfoNCE optimizes the probability of two views sharing the same source toward a constant target defined by this matrix, naturally inducing feature clustering in the representation space. Leveraging this insight, we propose Scaled Convergence InfoNCE (SC-InfoNCE), a novel loss function that introduces a tunable convergence target to flexibly control feature similarity alignment. By scaling the target matrix, SC-InfoNCE enables flexible control over feature similarity alignment, allowing the training objective to better match the statistical properties of downstream data. Experiments on benchmark datasets, including image, graph, and text tasks, show that SC-InfoNCE consistently achieves strong and reliable performance across diverse domains.

Graph Elimination Networks

Graph Neural Networks (GNNs) are widely applied across various domains, yet they perform poorly in deep layers. Existing research typically attributes this problem to node over-smoothing, where node representations become indistinguishable after multiple rounds of propagation. In this paper, we delve into the neighborhood propagation mechanism of GNNs and discover that the real root cause of GNNs' performance degradation in deep layers lies in ineffective neighborhood feature propagation. This propagation leads to an exponential growth of a node's current representation at every propagation step, making it extremely challenging to capture valuable dependencies between long-distance nodes. To address this issue, we introduce Graph Elimination Networks (GENs), which employ a specific algorithm to eliminate redundancies during neighborhood propagation. We demonstrate that GENs can enhance nodes' perception of distant neighborhoods and extend the depth of network propagation. Extensive experiments show that GENs outperform the state-of-the-art methods on various graph-level and node-level datasets.

Deep Maxout Network Gaussian Process

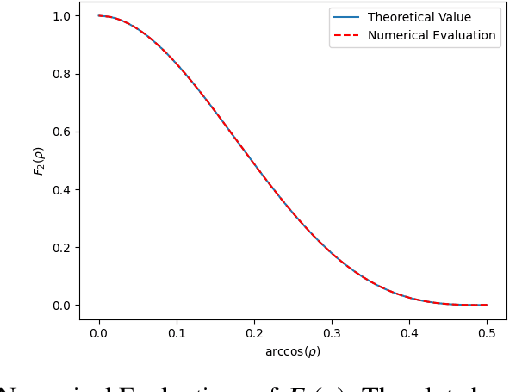
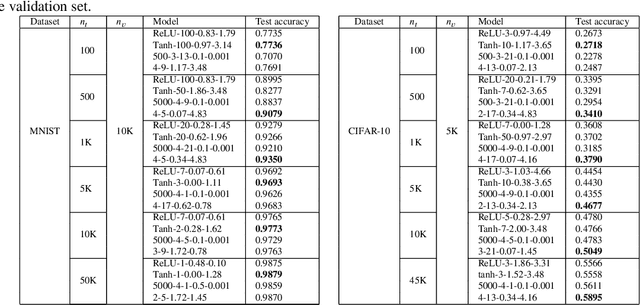
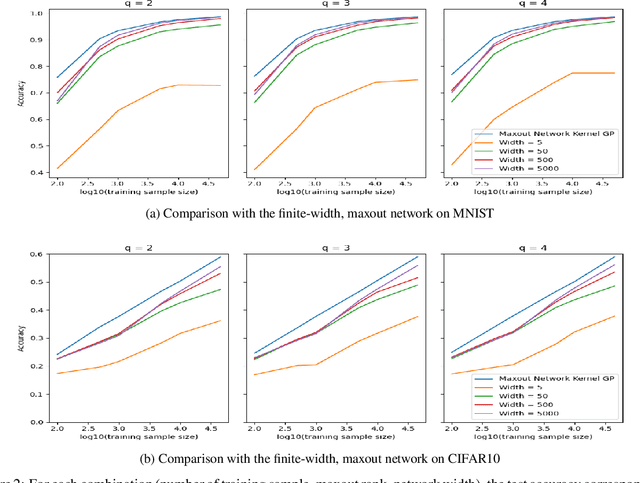
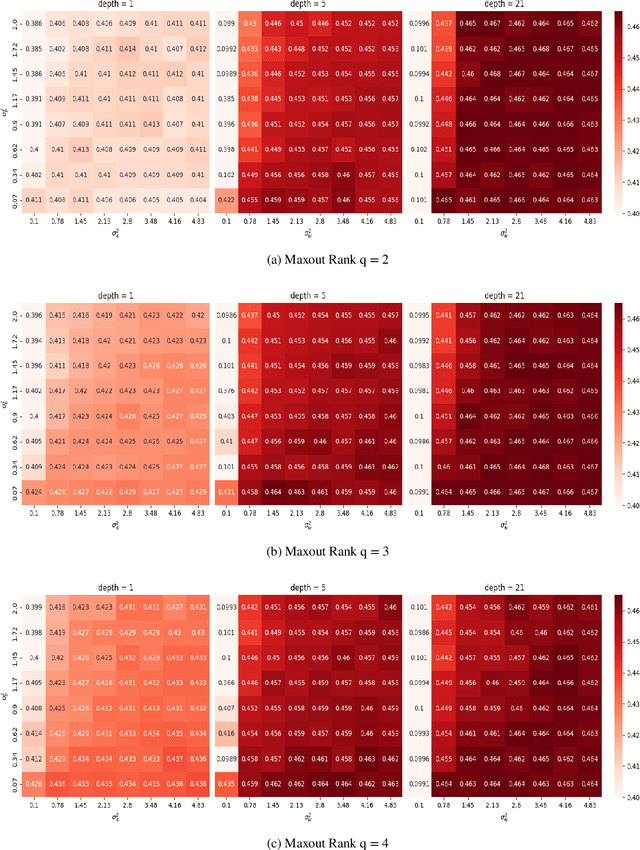
Study of neural networks with infinite width is important for better understanding of the neural network in practical application. In this work, we derive the equivalence of the deep, infinite-width maxout network and the Gaussian process (GP) and characterize the maxout kernel with a compositional structure. Moreover, we build up the connection between our deep maxout network kernel and deep neural network kernels. We also give an efficient numerical implementation of our kernel which can be adapted to any maxout rank. Numerical results show that doing Bayesian inference based on the deep maxout network kernel can lead to competitive results compared with their finite-width counterparts and deep neural network kernels. This enlightens us that the maxout activation may also be incorporated into other infinite-width neural network structures such as the convolutional neural network (CNN).