Permutation recovery of spikes in noisy high-dimensional tensor estimation

We study the dynamics of gradient flow in high dimensions for the multi-spiked tensor problem, where the goal is to estimate $r$ unknown signal vectors (spikes) from noisy Gaussian tensor observations. Specifically, we analyze the maximum likelihood estimation procedure, which involves optimizing a highly nonconvex random function. We determine the sample complexity required for gradient flow to efficiently recover all spikes, without imposing any assumptions on the separation of the signal-to-noise ratios (SNRs). More precisely, our results provide the sample complexity required to guarantee recovery of the spikes up to a permutation. Our work builds on our companion paper [Ben Arous, Gerbelot, Piccolo 2024], which studies Langevin dynamics and determines the sample complexity and separation conditions for the SNRs necessary for ensuring exact recovery of the spikes (where the recovered permutation matches the identity). During the recovery process, the correlations between the estimators and the hidden vectors increase in a sequential manner. The order in which these correlations become significant depends on their initial values and the corresponding SNRs, which ultimately determines the permutation of the recovered spikes.

Stochastic gradient descent in high dimensions for multi-spiked tensor PCA

We study the dynamics in high dimensions of online stochastic gradient descent for the multi-spiked tensor model. This multi-index model arises from the tensor principal component analysis (PCA) problem with multiple spikes, where the goal is to estimate $r$ unknown signal vectors within the $N$-dimensional unit sphere through maximum likelihood estimation from noisy observations of a $p$-tensor. We determine the number of samples and the conditions on the signal-to-noise ratios (SNRs) required to efficiently recover the unknown spikes from natural random initializations. We show that full recovery of all spikes is possible provided a number of sample scaling as $N^{p-2}$, matching the algorithmic threshold identified in the rank-one case [Ben Arous, Gheissari, Jagannath 2020, 2021]. Our results are obtained through a detailed analysis of a low-dimensional system that describes the evolution of the correlations between the estimators and the spikes, while controlling the noise in the dynamics. We find that the spikes are recovered sequentially in a process we term "sequential elimination": once a correlation exceeds a critical threshold, all correlations sharing a row or column index become sufficiently small, allowing the next correlation to grow and become macroscopic. The order in which correlations become macroscopic depends on their initial values and the corresponding SNRs, leading to either exact recovery or recovery of a permutation of the spikes. In the matrix case, when $p=2$, if the SNRs are sufficiently separated, we achieve exact recovery of the spikes, whereas equal SNRs lead to recovery of the subspace spanned by the spikes.

High-dimensional optimization for multi-spiked tensor PCA

We study the dynamics of two local optimization algorithms, online stochastic gradient descent (SGD) and gradient flow, within the framework of the multi-spiked tensor model in the high-dimensional regime. This multi-index model arises from the tensor principal component analysis (PCA) problem, which aims to infer $r$ unknown, orthogonal signal vectors within the $N$-dimensional unit sphere through maximum likelihood estimation from noisy observations of an order-$p$ tensor. We determine the number of samples and the conditions on the signal-to-noise ratios (SNRs) required to efficiently recover the unknown spikes from natural initializations. Specifically, we distinguish between three types of recovery: exact recovery of each spike, recovery of a permutation of all spikes, and recovery of the correct subspace spanned by the signal vectors. We show that with online SGD, it is possible to recover all spikes provided a number of sample scaling as $N^{p-2}$, aligning with the computational threshold identified in the rank-one tensor PCA problem [Ben Arous, Gheissari, Jagannath 2020, 2021]. For gradient flow, we show that the algorithmic threshold to efficiently recover the first spike is also of order $N^{p-2}$. However, recovering the subsequent directions requires the number of samples to scale as $N^{p-1}$. Our results are obtained through a detailed analysis of a low-dimensional system that describes the evolution of the correlations between the estimators and the spikes. In particular, the hidden vectors are recovered one by one according to a sequential elimination phenomenon: as one correlation exceeds a critical threshold, all correlations sharing a row or column index decrease and become negligible, allowing the subsequent correlation to grow and become macroscopic. The sequence in which correlations become macroscopic depends on their initial values and on the associated SNRs.

Long Random Matrices and Tensor Unfolding

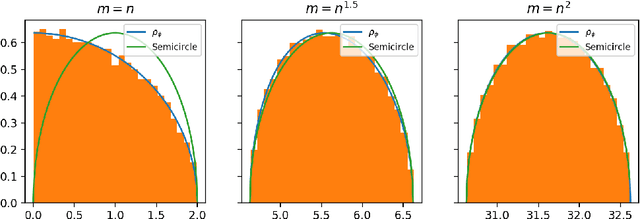
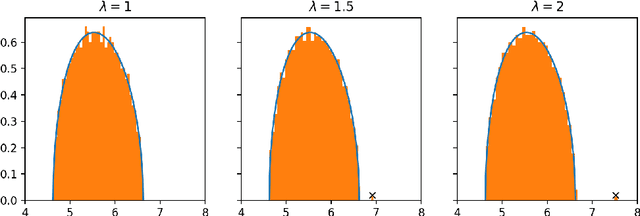
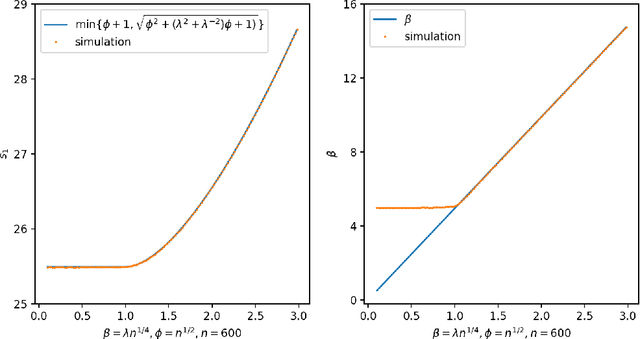
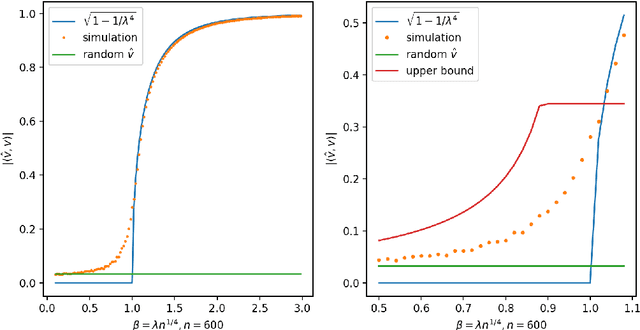
In this paper, we consider the singular values and singular vectors of low rank perturbations of large rectangular random matrices, in the regime the matrix is "long": we allow the number of rows (columns) to grow polynomially in the number of columns (rows). We prove there exists a critical signal-to-noise ratio (depending on the dimensions of the matrix), and the extreme singular values and singular vectors exhibit a BBP type phase transition. As a main application, we investigate the tensor unfolding algorithm for the asymmetric rank-one spiked tensor model, and obtain an exact threshold, which is independent of the procedure of tensor unfolding. If the signal-to-noise ratio is above the threshold, tensor unfolding detects the signals; otherwise, it fails to capture the signals.

Free Energy Wells and Overlap Gap Property in Sparse PCA

We study a variant of the sparse PCA (principal component analysis) problem in the "hard" regime, where the inference task is possible yet no polynomial-time algorithm is known to exist. Prior work, based on the low-degree likelihood ratio, has conjectured a precise expression for the best possible (sub-exponential) runtime throughout the hard regime. Following instead a statistical physics inspired point of view, we show bounds on the depth of free energy wells for various Gibbs measures naturally associated to the problem. These free energy wells imply hitting time lower bounds that corroborate the low-degree conjecture: we show that a class of natural MCMC (Markov chain Monte Carlo) methods (with worst-case initialization) cannot solve sparse PCA with less than the conjectured runtime. These lower bounds apply to a wide range of values for two tuning parameters: temperature and sparsity misparametrization. Finally, we prove that the Overlap Gap Property (OGP), a structural property that implies failure of certain local search algorithms, holds in a significant part of the hard regime.

Landscape Complexity for the Empirical Risk of Generalized Linear Models

We present a method to obtain the average and the typical value of the number of critical points of the empirical risk landscape for generalized linear estimation problems and variants. This represents a substantial extension of previous applications of the Kac-Rice method since it allows to analyze the critical points of high dimensional non-Gaussian random functions. We obtain a rigorous explicit variational formula for the annealed complexity, which is the logarithm of the average number of critical points at fixed value of the empirical risk. This result is simplified, and extended, using the non-rigorous Kac-Rice replicated method from theoretical physics. In this way we find an explicit variational formula for the quenched complexity, which is generally different from its annealed counterpart, and allows to obtain the number of critical points for typical instances up to exponential accuracy.

The Loss Surfaces of Multilayer Networks

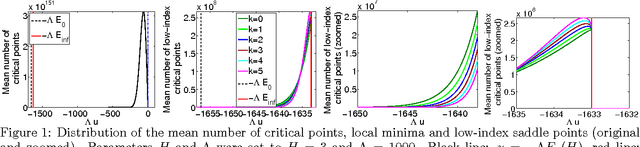
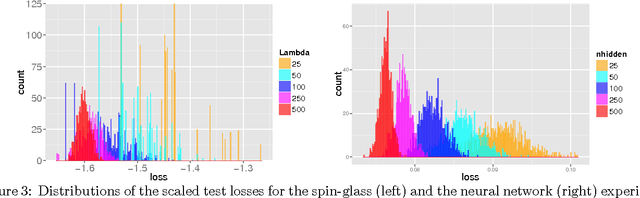
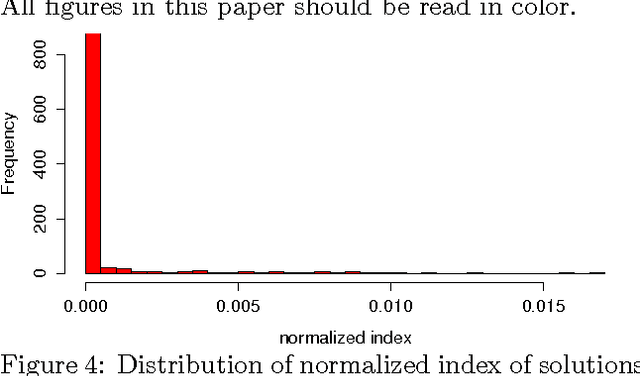
We study the connection between the highly non-convex loss function of a simple model of the fully-connected feed-forward neural network and the Hamiltonian of the spherical spin-glass model under the assumptions of: i) variable independence, ii) redundancy in network parametrization, and iii) uniformity. These assumptions enable us to explain the complexity of the fully decoupled neural network through the prism of the results from random matrix theory. We show that for large-size decoupled networks the lowest critical values of the random loss function form a layered structure and they are located in a well-defined band lower-bounded by the global minimum. The number of local minima outside that band diminishes exponentially with the size of the network. We empirically verify that the mathematical model exhibits similar behavior as the computer simulations, despite the presence of high dependencies in real networks. We conjecture that both simulated annealing and SGD converge to the band of low critical points, and that all critical points found there are local minima of high quality measured by the test error. This emphasizes a major difference between large- and small-size networks where for the latter poor quality local minima have non-zero probability of being recovered. Finally, we prove that recovering the global minimum becomes harder as the network size increases and that it is in practice irrelevant as global minimum often leads to overfitting.