Measuring multi-calibration

A suitable scalar metric can help measure multi-calibration, defined as follows. When the expected values of observed responses are equal to corresponding predicted probabilities, the probabilistic predictions are known as "perfectly calibrated." When the predicted probabilities are perfectly calibrated simultaneously across several subpopulations, the probabilistic predictions are known as "perfectly multi-calibrated." In practice, predicted probabilities are seldom perfectly multi-calibrated, so a statistic measuring the distance from perfect multi-calibration is informative. A recently proposed metric for calibration, based on the classical Kuiper statistic, is a natural basis for a new metric of multi-calibration and avoids well-known problems of metrics based on binning or kernel density estimation. The newly proposed metric weights the contributions of different subpopulations in proportion to their signal-to-noise ratios; data analyses' ablations demonstrate that the metric becomes noisy when omitting the signal-to-noise ratios from the metric. Numerical examples on benchmark data sets illustrate the new metric.

On the convergence of loss and uncertainty-based active learning algorithms

We study convergence rates of loss and uncertainty-based active learning algorithms under various assumptions. First, we provide a set of conditions under which a convergence rate guarantee holds, and use this for linear classifiers and linearly separable datasets to show convergence rate guarantees for loss-based sampling and different loss functions. Second, we provide a framework that allows us to derive convergence rate bounds for loss-based sampling by deploying known convergence rate bounds for stochastic gradient descent algorithms. Third, and last, we propose an active learning algorithm that combines sampling of points and stochastic Polyak's step size. We show a condition on the sampling that ensures a convergence rate guarantee for this algorithm for smooth convex loss functions. Our numerical results demonstrate efficiency of our proposed algorithm.

Using Neural Generative Models to Release Synthetic Twitter Corpora with Reduced Stylometric Identifiability of Users

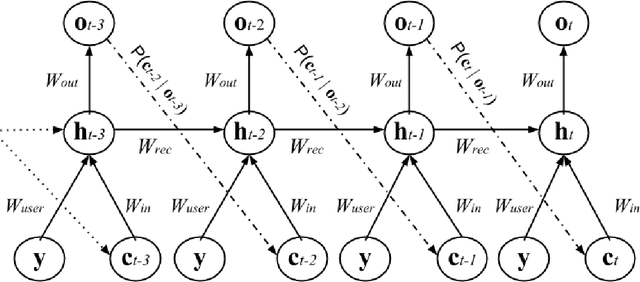
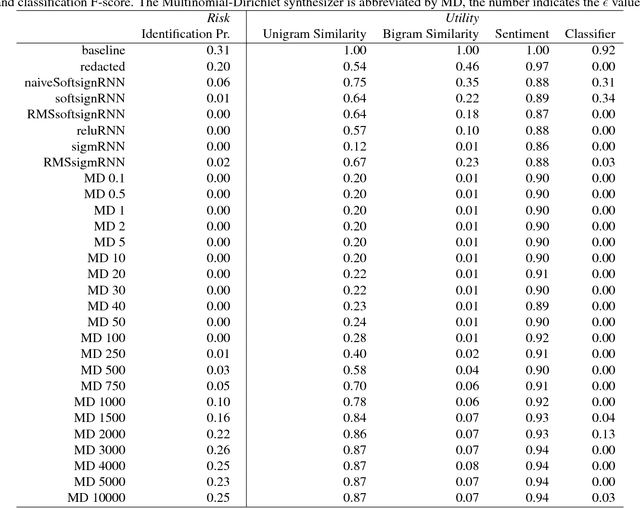
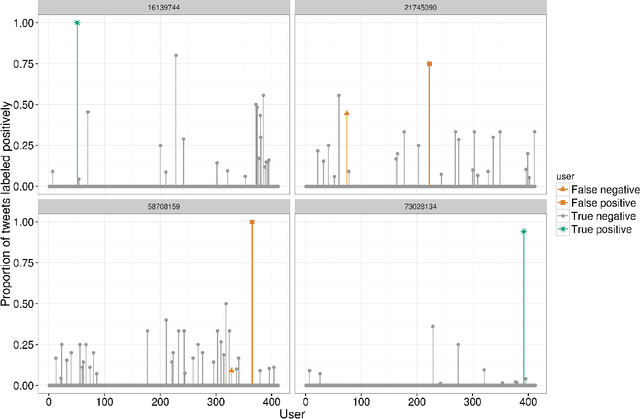
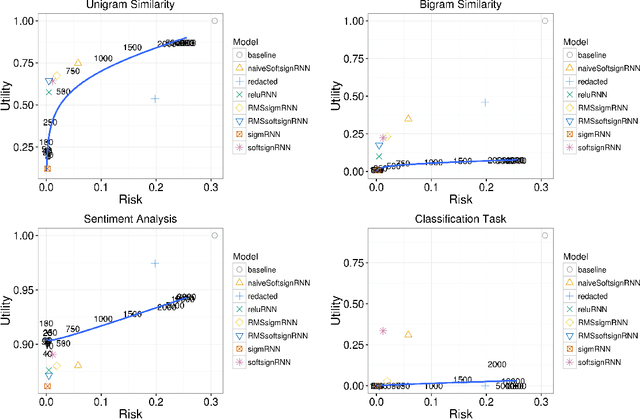
We present a method for generating synthetic versions of Twitter data using neural generative models. The goal is protecting individuals in the source data from stylometric re-identification attacks while still releasing data that carries research value. Specifically, we generate tweet corpora that maintain user-level word distributions by augmenting the neural language models with user-specific components. We compare our approach to two standard text data protection methods: redaction and iterative translation. We evaluate the three methods on measures of risk and utility. We define risk following the stylometric models of re-identification, and we define utility based on two general word distribution measures and two common text analysis research tasks. We find that neural models are able to significantly lower risk over previous methods with little cost to utility. We also demonstrate that the neural models allow data providers to actively control the risk-utility trade-off through model tuning parameters. This work presents promising results for a new tool addressing the problem of privacy for free text and sharing social media data in a way that respects privacy and is ethically responsible.