$\texttt{skwdro}$: a library for Wasserstein distributionally robust machine learning

We present skwdro, a Python library for training robust machine learning models. The library is based on distributionally robust optimization using optimal transport distances. For ease of use, it features both scikit-learn compatible estimators for popular objectives, as well as a wrapper for PyTorch modules, enabling researchers and practitioners to use it in a wide range of models with minimal code changes. Its implementation relies on an entropic smoothing of the original robust objective in order to ensure maximal model flexibility. The library is available at https://github.com/iutzeler/skwdro

What is the long-run distribution of stochastic gradient descent? A large deviations analysis

In this paper, we examine the long-run distribution of stochastic gradient descent (SGD) in general, non-convex problems. Specifically, we seek to understand which regions of the problem's state space are more likely to be visited by SGD, and by how much. Using an approach based on the theory of large deviations and randomly perturbed dynamical systems, we show that the long-run distribution of SGD resembles the Boltzmann-Gibbs distribution of equilibrium thermodynamics with temperature equal to the method's step-size and energy levels determined by the problem's objective and the statistics of the noise. In particular, we show that, in the long run, (a) the problem's critical region is visited exponentially more often than any non-critical region; (b) the iterates of SGD are exponentially concentrated around the problem's minimum energy state (which does not always coincide with the global minimum of the objective); (c) all other connected components of critical points are visited with frequency that is exponentially proportional to their energy level; and, finally (d) any component of local maximizers or saddle points is "dominated" by a component of local minimizers which is visited exponentially more often.

Derivatives of Stochastic Gradient Descent

We consider stochastic optimization problems where the objective depends on some parameter, as commonly found in hyperparameter optimization for instance. We investigate the behavior of the derivatives of the iterates of Stochastic Gradient Descent (SGD) with respect to that parameter and show that they are driven by an inexact SGD recursion on a different objective function, perturbed by the convergence of the original SGD. This enables us to establish that the derivatives of SGD converge to the derivative of the solution mapping in terms of mean squared error whenever the objective is strongly convex. Specifically, we demonstrate that with constant step-sizes, these derivatives stabilize within a noise ball centered at the solution derivative, and that with vanishing step-sizes they exhibit $O(\log(k)^2 / k)$ convergence rates. Additionally, we prove exponential convergence in the interpolation regime. Our theoretical findings are illustrated by numerical experiments on synthetic tasks.

Exact Generalization Guarantees for (Regularized) Wasserstein Distributionally Robust Models

Wasserstein distributionally robust estimators have emerged as powerful models for prediction and decision-making under uncertainty. These estimators provide attractive generalization guarantees: the robust objective obtained from the training distribution is an exact upper bound on the true risk with high probability. However, existing guarantees either suffer from the curse of dimensionality, are restricted to specific settings, or lead to spurious error terms. In this paper, we show that these generalization guarantees actually hold on general classes of models, do not suffer from the curse of dimensionality, and can even cover distribution shifts at testing. We also prove that these results carry over to the newly-introduced regularized versions of Wasserstein distributionally robust problems.

On the rate of convergence of Bregman proximal methods in constrained variational inequalities

We examine the last-iterate convergence rate of Bregman proximal methods - from mirror descent to mirror-prox - in constrained variational inequalities. Our analysis shows that the convergence speed of a given method depends sharply on the Legendre exponent of the underlying Bregman regularizer (Euclidean, entropic, or other), a notion that measures the growth rate of said regularizer near a solution. In particular, we show that boundary solutions exhibit a clear separation of regimes between methods with a zero and non-zero Legendre exponent respectively, with linear convergence for the former versus sublinear for the latter. This dichotomy becomes even more pronounced in linearly constrained problems where, specifically, Euclidean methods converge along sharp directions in a finite number of steps, compared to a linear rate for entropic methods.

Push--Pull with Device Sampling

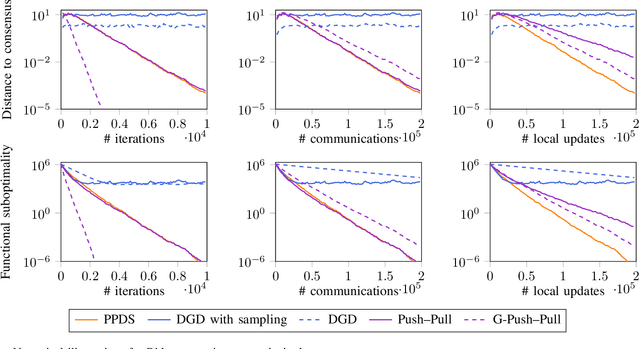
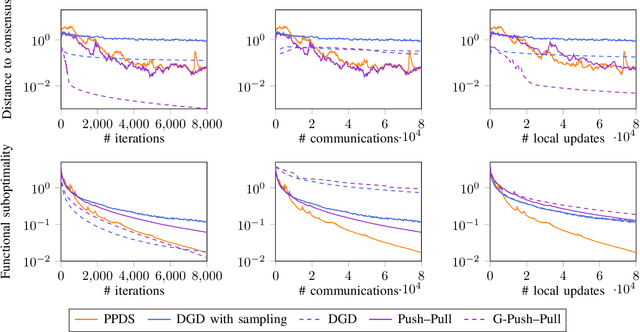
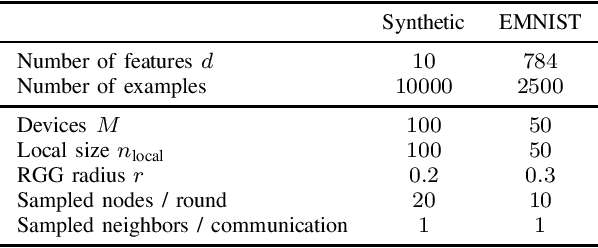
We consider decentralized optimization problems in which a number of agents collaborate to minimize the average of their local functions by exchanging over an underlying communication graph. Specifically, we place ourselves in an asynchronous model where only a random portion of nodes perform computation at each iteration, while the information exchange can be conducted between all the nodes and in an asymmetric fashion. For this setting, we propose an algorithm that combines gradient tracking and variance reduction over the entire network. This enables each node to track the average of the gradients of the objective functions. Our theoretical analysis shows that the algorithm converges linearly, when the local objective functions are strongly convex, under mild connectivity conditions on the expected mixing matrices. In particular, our result does not require the mixing matrices to be doubly stochastic. In the experiments, we investigate a broadcast mechanism that transmits information from computing nodes to their neighbors, and confirm the linear convergence of our method on both synthetic and real-world datasets.

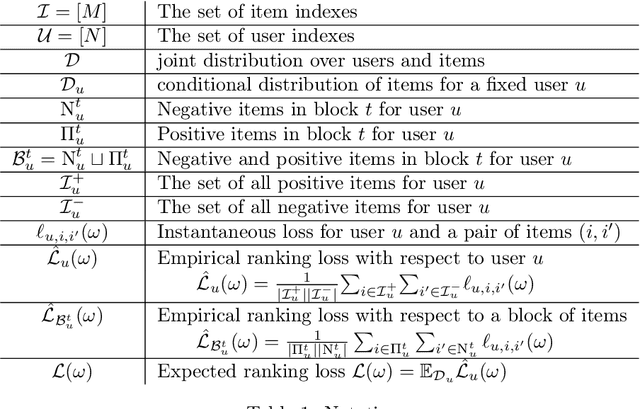
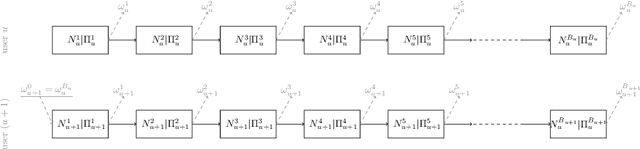
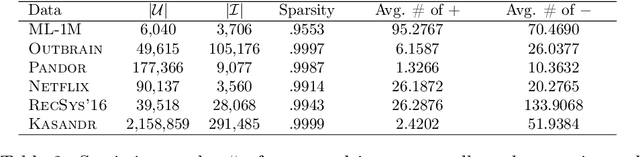
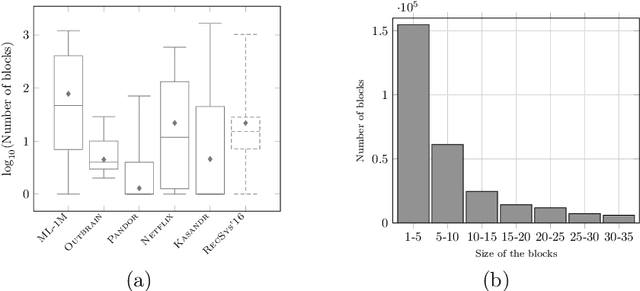
Learning over No-Preferred and Preferred Sequence of Items for Robust Recommendation (Extended Abstract)

This paper is an extended version of [Burashnikova et al., 2021, arXiv: 2012.06910], where we proposed a theoretically supported sequential strategy for training a large-scale Recommender System (RS) over implicit feedback, mainly in the form of clicks. The proposed approach consists in minimizing pairwise ranking loss over blocks of consecutive items constituted by a sequence of non-clicked items followed by a clicked one for each user. We present two variants of this strategy where model parameters are updated using either the momentum method or a gradient-based approach. To prevent updating the parameters for an abnormally high number of clicks over some targeted items (mainly due to bots), we introduce an upper and a lower threshold on the number of updates for each user. These thresholds are estimated over the distribution of the number of blocks in the training set. They affect the decision of RS by shifting the distribution of items that are shown to the users. Furthermore, we provide a convergence analysis of both algorithms and demonstrate their practical efficiency over six large-scale collections with respect to various ranking measures.

The Last-Iterate Convergence Rate of Optimistic Mirror Descent in Stochastic Variational Inequalities

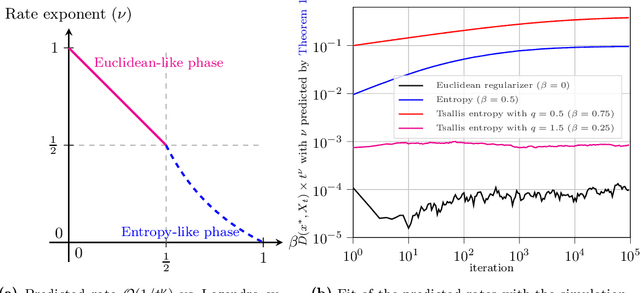
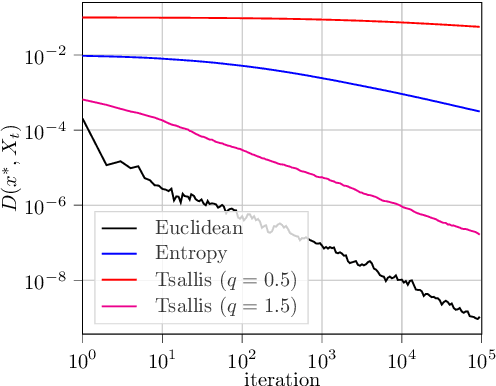
In this paper, we analyze the local convergence rate of optimistic mirror descent methods in stochastic variational inequalities, a class of optimization problems with important applications to learning theory and machine learning. Our analysis reveals an intricate relation between the algorithm's rate of convergence and the local geometry induced by the method's underlying Bregman function. We quantify this relation by means of the Legendre exponent, a notion that we introduce to measure the growth rate of the Bregman divergence relative to the ambient norm near a solution. We show that this exponent determines both the optimal step-size policy of the algorithm and the optimal rates attained, explaining in this way the differences observed for some popular Bregman functions (Euclidean projection, negative entropy, fractional power, etc.).

Optimization in Open Networks via Dual Averaging

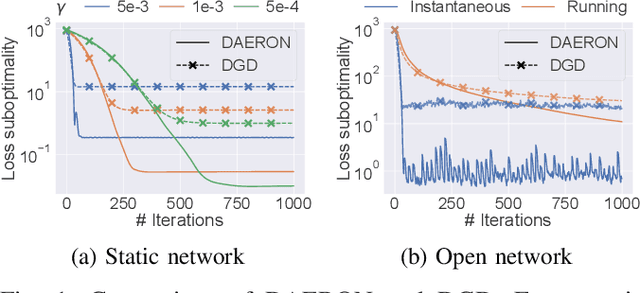
In networks of autonomous agents (e.g., fleets of vehicles, scattered sensors), the problem of minimizing the sum of the agents' local functions has received a lot of interest. We tackle here this distributed optimization problem in the case of open networks when agents can join and leave the network at any time. Leveraging recent online optimization techniques, we propose and analyze the convergence of a decentralized asynchronous optimization method for open networks.

Multi-Agent Online Optimization with Delays: Asynchronicity, Adaptivity, and Optimism

Online learning has been successfully applied to many problems in which data are revealed over time. In this paper, we provide a general framework for studying multi-agent online learning problems in the presence of delays and asynchronicities. Specifically, we propose and analyze a class of adaptive dual averaging schemes in which agents only need to accumulate gradient feedback received from the whole system, without requiring any between-agent coordination. In the single-agent case, the adaptivity of the proposed method allows us to extend a range of existing results to problems with potentially unbounded delays between playing an action and receiving the corresponding feedback. In the multi-agent case, the situation is significantly more complicated because agents may not have access to a global clock to use as a reference point; to overcome this, we focus on the information that is available for producing each prediction rather than the actual delay associated with each feedback. This allows us to derive adaptive learning strategies with optimal regret bounds, at both the agent and network levels. Finally, we also analyze an "optimistic" variant of the proposed algorithm which is capable of exploiting the predictability of problems with a slower variation and leads to improved regret bounds.