Numerically robust Gaussian state estimation with singular observation noise

This article proposes numerically robust algorithms for Gaussian state estimation with singular observation noise. Our approach combines a series of basis changes with Bayes' rule, transforming the singular estimation problem into a nonsingular one with reduced state dimension. In addition to ensuring low runtime and numerical stability, our proposal facilitates marginal-likelihood computations and Gauss-Markov representations of the posterior process. We analyse the proposed method's computational savings and numerical robustness and validate our findings in a series of simulations.

Propagating Model Uncertainty through Filtering-based Probabilistic Numerical ODE Solvers

Filtering-based probabilistic numerical solvers for ordinary differential equations (ODEs), also known as ODE filters, have been established as efficient methods for quantifying numerical uncertainty in the solution of ODEs. In practical applications, however, the underlying dynamical system often contains uncertain parameters, requiring the propagation of this model uncertainty to the ODE solution. In this paper, we demonstrate that ODE filters, despite their probabilistic nature, do not automatically solve this uncertainty propagation problem. To address this limitation, we present a novel approach that combines ODE filters with numerical quadrature to properly marginalize over uncertain parameters, while accounting for both parameter uncertainty and numerical solver uncertainty. Experiments across multiple dynamical systems demonstrate that the resulting uncertainty estimates closely match reference solutions. Notably, we show how the numerical uncertainty from the ODE solver can help prevent overconfidence in the propagated uncertainty estimates, especially when using larger step sizes. Our results illustrate that probabilistic numerical methods can effectively quantify both numerical and parametric uncertainty in dynamical systems.

The two filter formula reconsidered: Smoothing in partially observed Gauss--Markov models without information parametrization

In this article, the two filter formula is re-examined in the setting of partially observed Gauss--Markov models. It is traditionally formulated as a filter running backward in time, where the Gaussian density is parametrized in ``information form''. However, the quantity in the backward recursion is strictly speaking not a distribution, but a likelihood. Taking this observation seriously, a recursion over log-quadratic likelihoods is formulated instead, which obviates the need for ``information'' parametrization. In particular, it greatly simplifies the square-root formulation of the algorithm. Furthermore, formulae are given for producing the forward Markov representation of the a posteriori distribution over paths from the proposed likelihood representation.

Parallel-in-Time Probabilistic Numerical ODE Solvers

Probabilistic numerical solvers for ordinary differential equations (ODEs) treat the numerical simulation of dynamical systems as problems of Bayesian state estimation. Aside from producing posterior distributions over ODE solutions and thereby quantifying the numerical approximation error of the method itself, one less-often noted advantage of this formalism is the algorithmic flexibility gained by formulating numerical simulation in the framework of Bayesian filtering and smoothing. In this paper, we leverage this flexibility and build on the time-parallel formulation of iterated extended Kalman smoothers to formulate a parallel-in-time probabilistic numerical ODE solver. Instead of simulating the dynamical system sequentially in time, as done by current probabilistic solvers, the proposed method processes all time steps in parallel and thereby reduces the span cost from linear to logarithmic in the number of time steps. We demonstrate the effectiveness of our approach on a variety of ODEs and compare it to a range of both classic and probabilistic numerical ODE solvers.

The Rank-Reduced Kalman Filter: Approximate Dynamical-Low-Rank Filtering In High Dimensions

Inference and simulation in the context of high-dimensional dynamical systems remain computationally challenging problems. Some form of dimensionality reduction is required to make the problem tractable in general. In this paper, we propose a novel approximate Gaussian filtering and smoothing method which propagates low-rank approximations of the covariance matrices. This is accomplished by projecting the Lyapunov equations associated with the prediction step to a manifold of low-rank matrices, which are then solved by a recently developed, numerically stable, dynamical low-rank integrator. Meanwhile, the update steps are made tractable by noting that the covariance update only transforms the column space of the covariance matrix, which is low-rank by construction. The algorithm differentiates itself from existing ensemble-based approaches in that the low-rank approximations of the covariance matrices are deterministic, rather than stochastic. Crucially, this enables the method to reproduce the exact Kalman filter as the low-rank dimension approaches the true dimensionality of the problem. Our method reduces computational complexity from cubic (for the Kalman filter) to \emph{quadratic} in the state-space size in the worst-case, and can achieve \emph{linear} complexity if the state-space model satisfies certain criteria. Through a set of experiments in classical data-assimilation and spatio-temporal regression, we show that the proposed method consistently outperforms the ensemble-based methods in terms of error in the mean and covariance with respect to the exact Kalman filter. This comes at no additional cost in terms of asymptotic computational complexity.

Probabilistic Exponential Integrators

Probabilistic solvers provide a flexible and efficient framework for simulation, uncertainty quantification, and inference in dynamical systems. However, like standard solvers, they suffer performance penalties for certain stiff systems, where small steps are required not for reasons of numerical accuracy but for the sake of stability. This issue is greatly alleviated in semi-linear problems by the probabilistic exponential integrators developed in this paper. By including the fast, linear dynamics in the prior, we arrive at a class of probabilistic integrators with favorable properties. Namely, they are proven to be L-stable, and in a certain case reduce to a classic exponential integrator -- with the added benefit of providing a probabilistic account of the numerical error. The method is also generalized to arbitrary non-linear systems by imposing piece-wise semi-linearity on the prior via Jacobians of the vector field at the previous estimates, resulting in probabilistic exponential Rosenbrock methods. We evaluate the proposed methods on multiple stiff differential equations and demonstrate their improved stability and efficiency over established probabilistic solvers. The present contribution thus expands the range of problems that can be effectively tackled within probabilistic numerics.

Orthonormal Expansions for Translation-Invariant Kernels

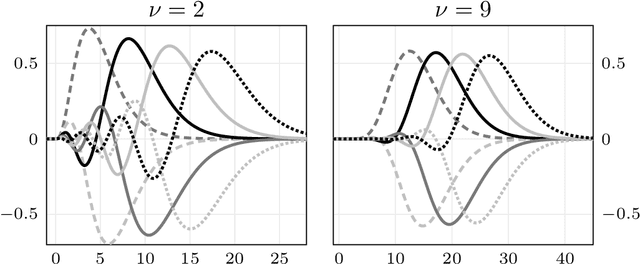
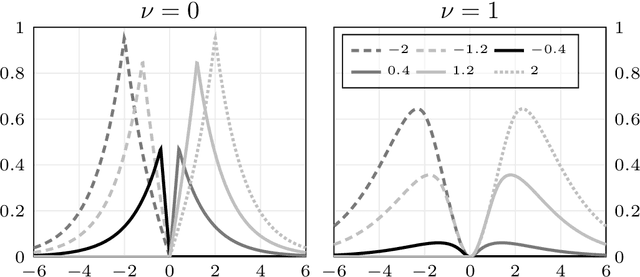
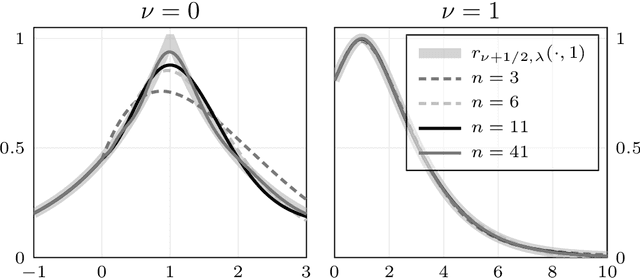
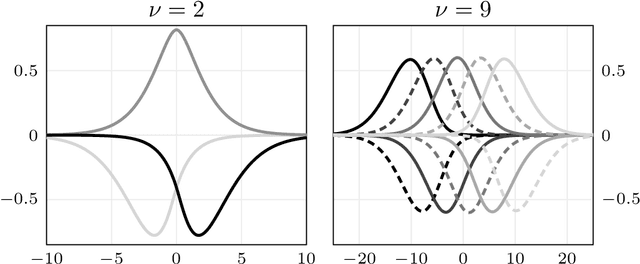
We present a general Fourier analytic technique for constructing orthonormal basis expansions of translation-invariant kernels from orthonormal bases of $\mathscr{L}_2(\mathbb{R})$. This allows us to derive explicit expansions on the real line for (i) Mat\'ern kernels of all half-integer orders in terms of associated Laguerre functions, (ii) the Cauchy kernel in terms of rational functions, and (iii) the Gaussian kernel in terms of Hermite functions.

Fenrir: Physics-Enhanced Regression for Initial Value Problems

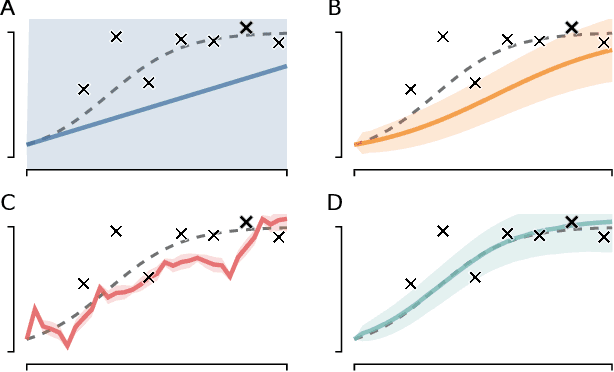
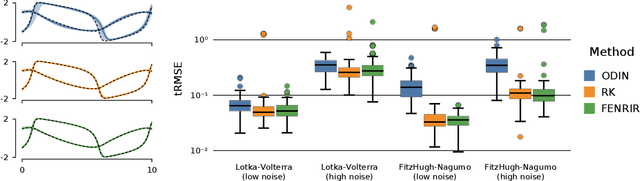
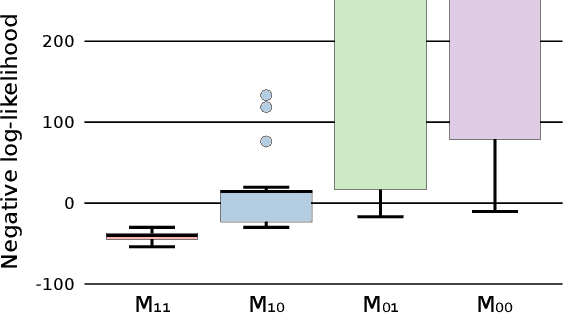
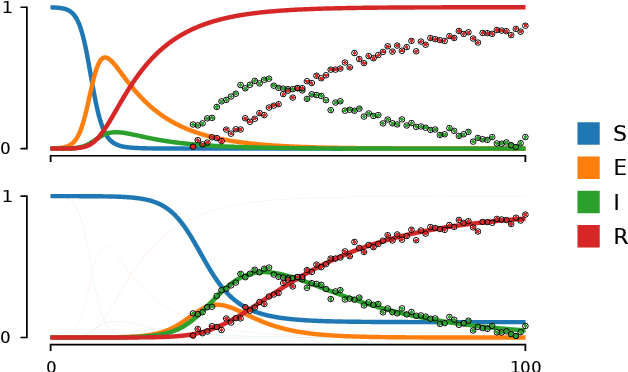
We show how probabilistic numerics can be used to convert an initial value problem into a Gauss--Markov process parametrised by the dynamics of the initial value problem. Consequently, the often difficult problem of parameter estimation in ordinary differential equations is reduced to hyperparameter estimation in Gauss--Markov regression, which tends to be considerably easier. The method's relation and benefits in comparison to classical numerical integration and gradient matching approaches is elucidated. In particular, the method can, in contrast to gradient matching, handle partial observations, and has certain routes for escaping local optima not available to classical numerical integration. Experimental results demonstrate that the method is on par or moderately better than competing approaches.

Pick-and-Mix Information Operators for Probabilistic ODE Solvers

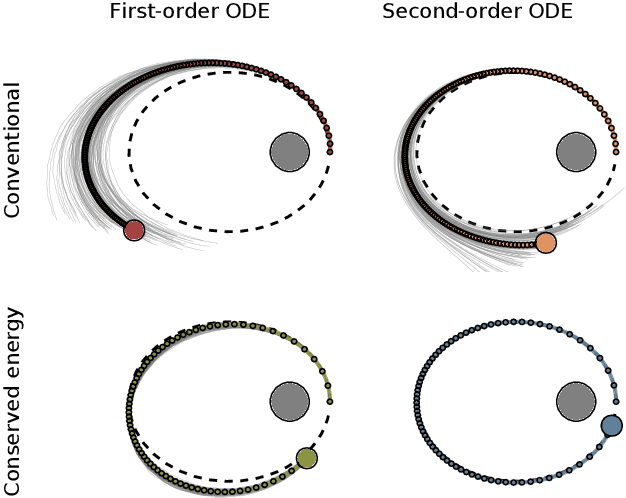
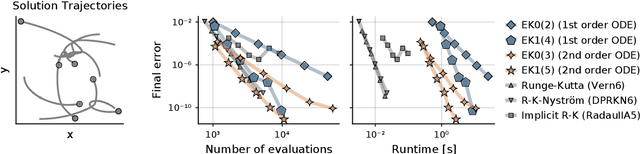
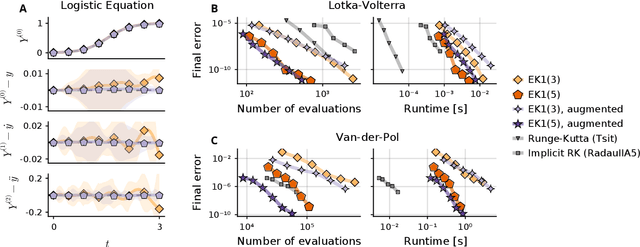
Probabilistic numerical solvers for ordinary differential equations compute posterior distributions over the solution of an initial value problem via Bayesian inference. In this paper, we leverage their probabilistic formulation to seamlessly include additional information as general likelihood terms. We show that second-order differential equations should be directly provided to the solver, instead of transforming the problem to first order. Additionally, by including higher-order information or physical conservation laws in the model, solutions become more accurate and more physically meaningful. Lastly, we demonstrate the utility of flexible information operators by solving differential-algebraic equations. In conclusion, the probabilistic formulation of numerical solvers offers a flexible way to incorporate various types of information, thus improving the resulting solutions.

A Probabilistic Taylor Expansion with Applications in Filtering and Differential Equations

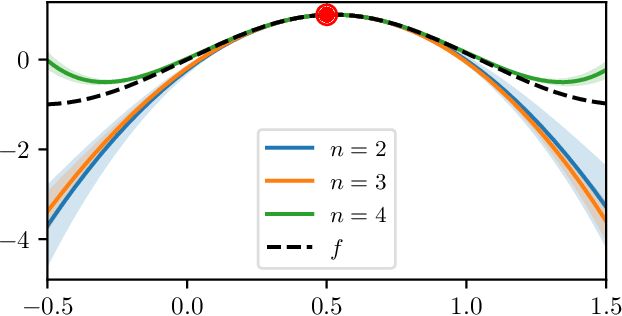
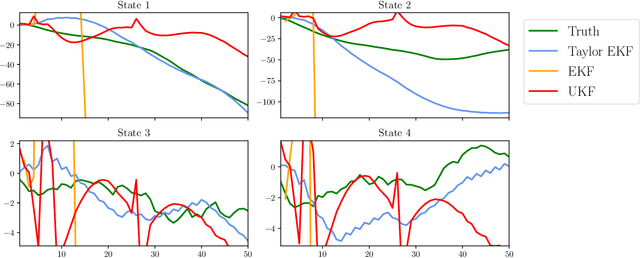
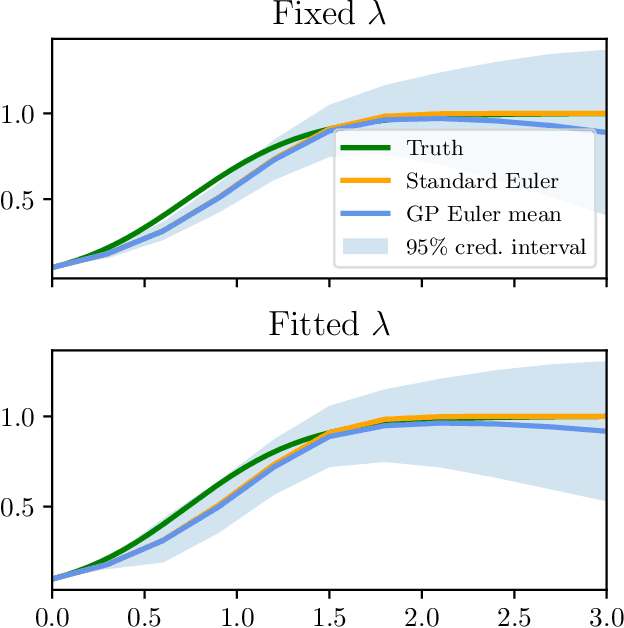
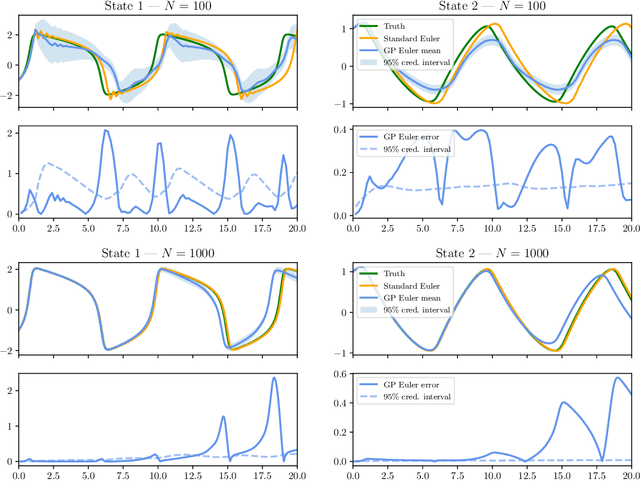
We study a class of Gaussian processes for which the posterior mean, for a particular choice of data, replicates a truncated Taylor expansion of any order. The data consists of derivative evaluations at the expansion point and the prior covariance kernel belongs to the class of Taylor kernels, which can be written in a certain power series form. This permits statistical modelling of the uncertainty in a variety of algorithms that exploit first and second order Taylor expansions. To demonstrate the utility of this Gaussian process model we introduce new probabilistic versions of the classical extended Kalman filter for non-linear state estimation and the Euler method for solving ordinary differential equations.