Recursive Nested Filtering for Efficient Amortized Bayesian Experimental Design

This paper introduces the Inside-Out Nested Particle Filter (IO-NPF), a novel, fully recursive, algorithm for amortized sequential Bayesian experimental design in the non-exchangeable setting. We frame policy optimization as maximum likelihood estimation in a non-Markovian state-space model, achieving (at most) $\mathcal{O}(T^2)$ computational complexity in the number of experiments. We provide theoretical convergence guarantees and introduce a backward sampling algorithm to reduce trajectory degeneracy. IO-NPF offers a practical, extensible, and provably consistent approach to sequential Bayesian experimental design, demonstrating improved efficiency over existing methods.

Conditioning diffusion models by explicit forward-backward bridging

Given an unconditional diffusion model $\pi(x, y)$, using it to perform conditional simulation $\pi(x \mid y)$ is still largely an open question and is typically achieved by learning conditional drifts to the denoising SDE after the fact. In this work, we express conditional simulation as an inference problem on an augmented space corresponding to a partial SDE bridge. This perspective allows us to implement efficient and principled particle Gibbs and pseudo-marginal samplers marginally targeting the conditional distribution $\pi(x \mid y)$. Contrary to existing methodology, our methods do not introduce any additional approximation to the unconditional diffusion model aside from the Monte Carlo error. We showcase the benefits and drawbacks of our approach on a series of synthetic and real data examples.

BlackJAX: Composable Bayesian inference in JAX

BlackJAX is a library implementing sampling and variational inference algorithms commonly used in Bayesian computation. It is designed for ease of use, speed, and modularity by taking a functional approach to the algorithms' implementation. BlackJAX is written in Python, using JAX to compile and run NumpPy-like samplers and variational methods on CPUs, GPUs, and TPUs. The library integrates well with probabilistic programming languages by working directly with the (un-normalized) target log density function. BlackJAX is intended as a collection of low-level, composable implementations of basic statistical 'atoms' that can be combined to perform well-defined Bayesian inference, but also provides high-level routines for ease of use. It is designed for users who need cutting-edge methods, researchers who want to create complex sampling methods, and people who want to learn how these work.

Nesting Particle Filters for Experimental Design in Dynamical Systems

In this paper, we propose a novel approach to Bayesian Experimental Design (BED) for non-exchangeable data that formulates it as risk-sensitive policy optimization. We develop the Inside-Out SMC^2 algorithm that uses a nested sequential Monte Carlo (SMC) estimator of the expected information gain and embeds it into a particle Markov chain Monte Carlo (pMCMC) framework to perform gradient-based policy optimization. This is in contrast to recent approaches that rely on biased estimators of the expected information gain (EIG) to amortize the cost of experiments by learning a design policy in advance. Numerical validation on a set of dynamical systems showcases the efficacy of our method in comparison to other state-of-the-art strategies.

Particle-MALA and Particle-mGRAD: Gradient-based MCMC methods for high-dimensional state-space models

State-of-the-art methods for Bayesian inference in state-space models are (a) conditional sequential Monte Carlo (CSMC) algorithms; (b) sophisticated 'classical' MCMC algorithms like MALA, or mGRAD from Titsias and Papaspiliopoulos (2018, arXiv:1610.09641v3 [stat.ML]). The former propose $N$ particles at each time step to exploit the model's 'decorrelation-over-time' property and thus scale favourably with the time horizon, $T$ , but break down if the dimension of the latent states, $D$, is large. The latter leverage gradient-/prior-informed local proposals to scale favourably with $D$ but exhibit sub-optimal scalability with $T$ due to a lack of model-structure exploitation. We introduce methods which combine the strengths of both approaches. The first, Particle-MALA, spreads $N$ particles locally around the current state using gradient information, thus extending MALA to $T > 1$ time steps and $N > 1$ proposals. The second, Particle-mGRAD, additionally incorporates (conditionally) Gaussian prior dynamics into the proposal, thus extending the mGRAD algorithm to $T > 1$ time steps and $N > 1$ proposals. We prove that Particle-mGRAD interpolates between CSMC and Particle-MALA, resolving the 'tuning problem' of choosing between CSMC (superior for highly informative prior dynamics) and Particle-MALA (superior for weakly informative prior dynamics). We similarly extend other 'classical' MCMC approaches like auxiliary MALA, aGRAD, and preconditioned Crank-Nicolson-Langevin (PCNL) to $T > 1$ time steps and $N > 1$ proposals. In experiments, for both highly and weakly informative prior dynamics, our methods substantially improve upon both CSMC and sophisticated 'classical' MCMC approaches.

Risk-Sensitive Stochastic Optimal Control as Rao-Blackwellized Markovian Score Climbing

Stochastic optimal control of dynamical systems is a crucial challenge in sequential decision-making. Recently, control-as-inference approaches have had considerable success, providing a viable risk-sensitive framework to address the exploration-exploitation dilemma. Nonetheless, a majority of these techniques only invoke the inference-control duality to derive a modified risk objective that is then addressed within a reinforcement learning framework. This paper introduces a novel perspective by framing risk-sensitive stochastic control as Markovian score climbing under samples drawn from a conditional particle filter. Our approach, while purely inference-centric, provides asymptotically unbiased estimates for gradient-based policy optimization with optimal importance weighting and no explicit value function learning. To validate our methodology, we apply it to the task of learning neural non-Gaussian feedback policies, showcasing its efficacy on numerical benchmarks of stochastic dynamical systems.

Parallel-in-Time Probabilistic Numerical ODE Solvers

Probabilistic numerical solvers for ordinary differential equations (ODEs) treat the numerical simulation of dynamical systems as problems of Bayesian state estimation. Aside from producing posterior distributions over ODE solutions and thereby quantifying the numerical approximation error of the method itself, one less-often noted advantage of this formalism is the algorithmic flexibility gained by formulating numerical simulation in the framework of Bayesian filtering and smoothing. In this paper, we leverage this flexibility and build on the time-parallel formulation of iterated extended Kalman smoothers to formulate a parallel-in-time probabilistic numerical ODE solver. Instead of simulating the dynamical system sequentially in time, as done by current probabilistic solvers, the proposed method processes all time steps in parallel and thereby reduces the span cost from linear to logarithmic in the number of time steps. We demonstrate the effectiveness of our approach on a variety of ODEs and compare it to a range of both classic and probabilistic numerical ODE solvers.

Auxiliary MCMC and particle Gibbs samplers for parallelisable inference in latent dynamical systems

We introduce two new classes of exact Markov chain Monte Carlo (MCMC) samplers for inference in latent dynamical models. The first one, which we coin auxiliary Kalman samplers, relies on finding a linear Gaussian state-space model approximation around the running trajectory corresponding to the state of the Markov chain. The second, that we name auxiliary particle Gibbs samplers corresponds to deriving good local proposals in an auxiliary Feynman--Kac model for use in particle Gibbs. Both samplers are controlled by augmenting the target distribution with auxiliary observations, resulting in an efficient Gibbs sampling routine. We discuss the relative statistical and computational performance of the samplers introduced, and show how to parallelise the auxiliary samplers along the time dimension. We illustrate the respective benefits and drawbacks of the resulting algorithms on classical examples from the particle filtering literature.

De-Sequentialized Monte Carlo: a parallel-in-time particle smoother

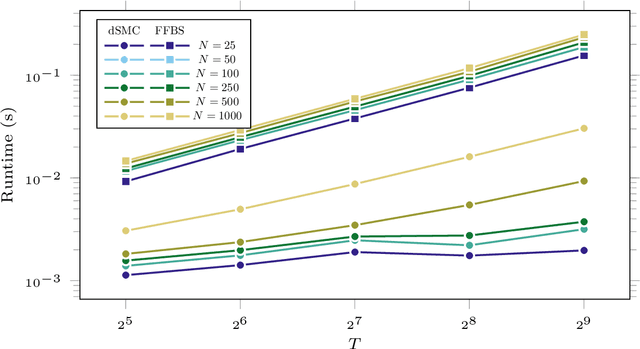
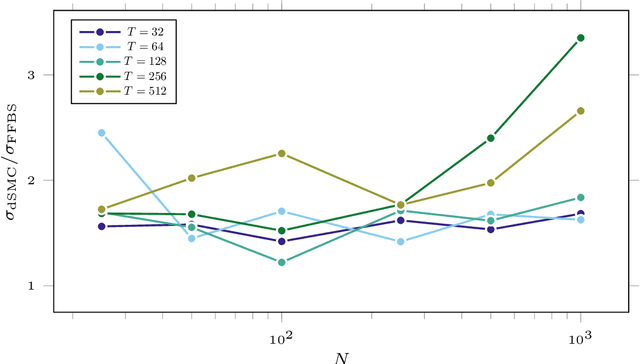
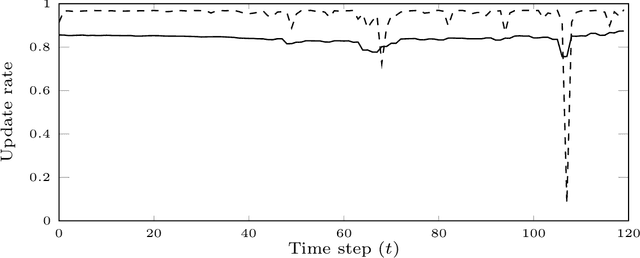
Particle smoothers are SMC (Sequential Monte Carlo) algorithms designed to approximate the joint distribution of the states given observations from a state-space model. We propose dSMC (de-Sequentialized Monte Carlo), a new particle smoother that is able to process $T$ observations in $\mathcal{O}(\log T)$ time on parallel architecture. This compares favourably with standard particle smoothers, the complexity of which is linear in $T$. We derive $\mathcal{L}_p$ convergence results for dSMC, with an explicit upper bound, polynomial in $T$. We then discuss how to reduce the variance of the smoothing estimates computed by dSMC by (i) designing good proposal distributions for sampling the particles at the initialization of the algorithm, as well as by (ii) using lazy resampling to increase the number of particles used in dSMC. Finally, we design a particle Gibbs sampler based on dSMC, which is able to perform parameter inference in a state-space model at a $\mathcal{O}(\log(T))$ cost on parallel hardware.

Gaussian Process Regression in Logarithmic Time

The aim of this article is to present a novel parallelization method for temporal Gaussian process (GP) regression problems. The method allows for solving GP regression problems in logarithmic $O(\log N)$ time, where $N$ is the number of time steps. Our approach uses the state-space representation of GPs which in its original form allows for linear $O(N)$ time GP regression by leveraging the Kalman filtering and smoothing methods. By using a recently proposed parallelization method for Bayesian filters and smoothers, we are able to reduce the linear computational complexity of the Kalman filter and smoother solutions to the GP regression problems into logarithmic span complexity, which transforms into logarithm time complexity when implemented in parallel hardware such as a graphics processing unit (GPU). We experimentally demonstrate the computational benefits one simulated and real datasets via our open-source implementation leveraging the GPflow framework.