Acceleration of Large Margin Metric Learning for Nearest Neighbor Classification Using Triplet Mining and Stratified Sampling

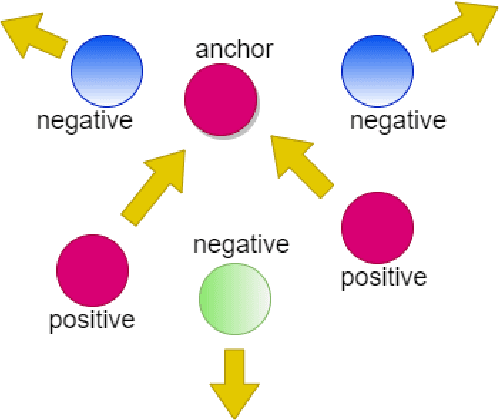
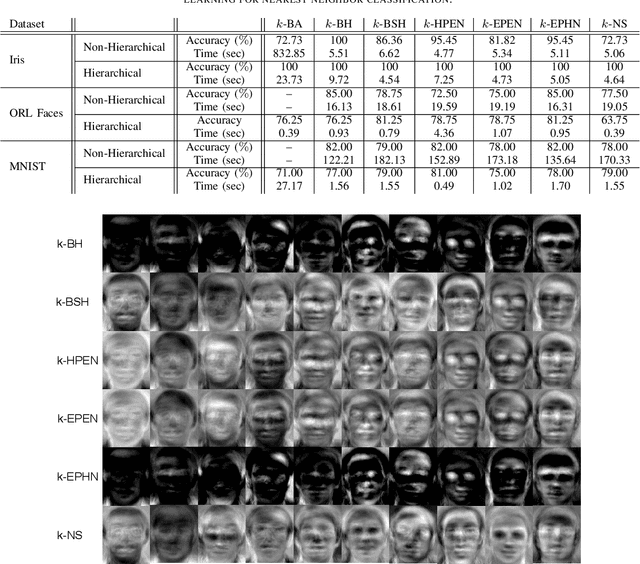
Metric learning is one of the techniques in manifold learning with the goal of finding a projection subspace for increasing and decreasing the inter- and intra-class variances, respectively. Some of the metric learning methods are based on triplet learning with anchor-positive-negative triplets. Large margin metric learning for nearest neighbor classification is one of the fundamental methods to do this. Recently, Siamese networks have been introduced with the triplet loss. Many triplet mining methods have been developed for Siamese networks; however, these techniques have not been applied on the triplets of large margin metric learning for nearest neighbor classification. In this work, inspired by the mining methods for Siamese networks, we propose several triplet mining techniques for large margin metric learning. Moreover, a hierarchical approach is proposed, for acceleration and scalability of optimization, where triplets are selected by stratified sampling in hierarchical hyper-spheres. We analyze the proposed methods on three publicly available datasets, i.e., Fisher Iris, ORL faces, and MNIST datasets.

Stochastic Neighbor Embedding with Gaussian and Student-t Distributions: Tutorial and Survey

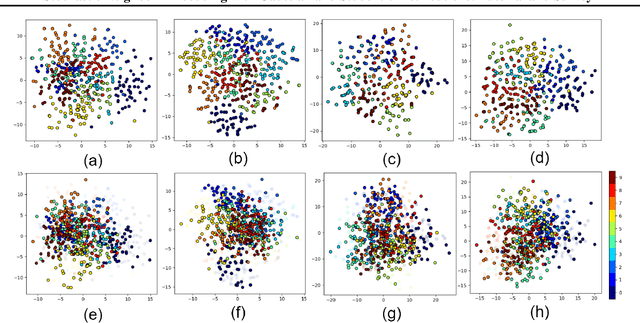
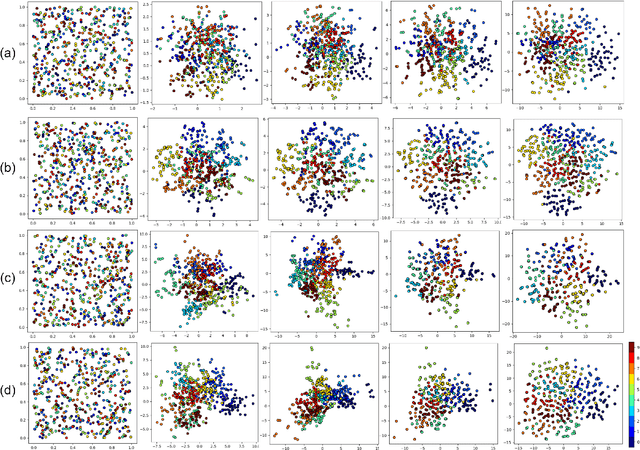
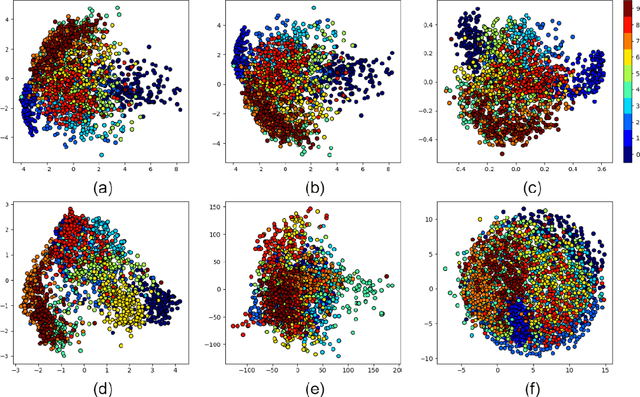
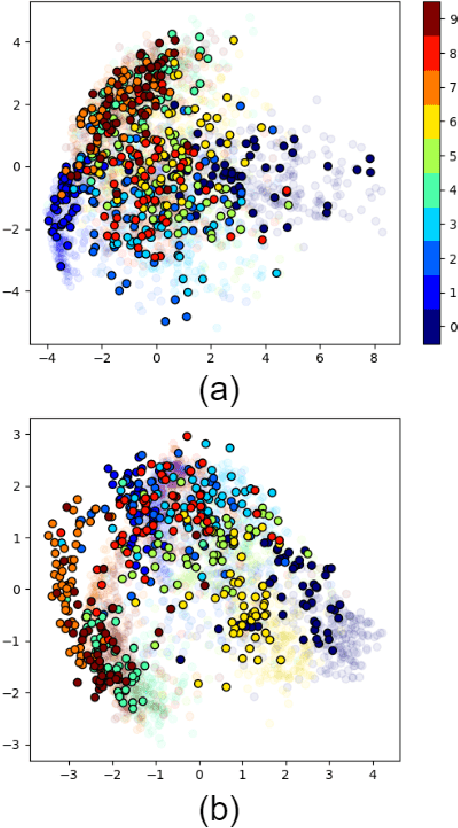
Stochastic Neighbor Embedding (SNE) is a manifold learning and dimensionality reduction method with a probabilistic approach. In SNE, every point is consider to be the neighbor of all other points with some probability and this probability is tried to be preserved in the embedding space. SNE considers Gaussian distribution for the probability in both the input and embedding spaces. However, t-SNE uses the Student-t and Gaussian distributions in these spaces, respectively. In this tutorial and survey paper, we explain SNE, symmetric SNE, t-SNE (or Cauchy-SNE), and t-SNE with general degrees of freedom. We also cover the out-of-sample extension and acceleration for these methods. Some simulations to visualize the embeddings are also provided.

Multidimensional Scaling, Sammon Mapping, and Isomap: Tutorial and Survey

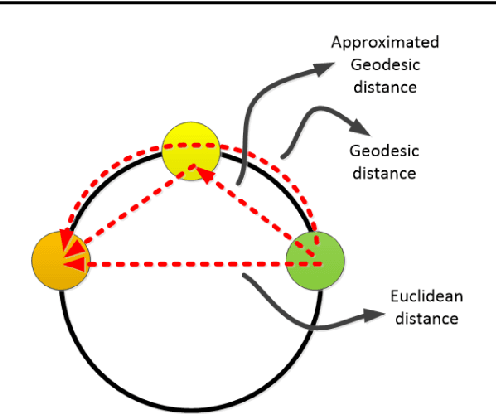
Multidimensional Scaling (MDS) is one of the first fundamental manifold learning methods. It can be categorized into several methods, i.e., classical MDS, kernel classical MDS, metric MDS, and non-metric MDS. Sammon mapping and Isomap can be considered as special cases of metric MDS and kernel classical MDS, respectively. In this tutorial and survey paper, we review the theory of MDS, Sammon mapping, and Isomap in detail. We explain all the mentioned categories of MDS. Then, Sammon mapping, Isomap, and kernel Isomap are explained. Out-of-sample embedding for MDS and Isomap using eigenfunctions and kernel mapping are introduced. Then, Nystrom approximation and its use in landmark MDS and landmark Isomap are introduced for big data embedding. We also provide some simulations for illustrating the embedding by these methods.

A Review on Deep Learning Techniques for the Diagnosis of Novel Coronavirus

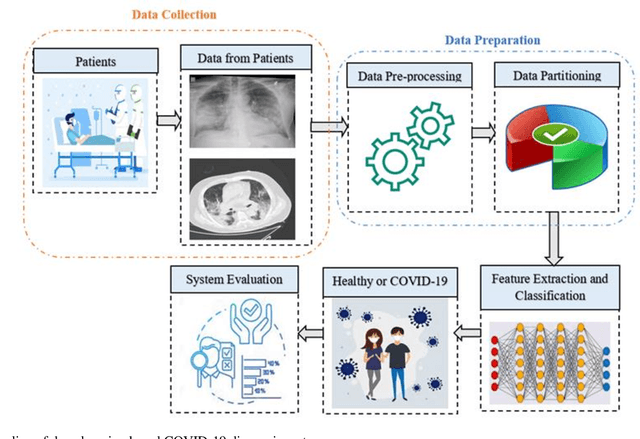
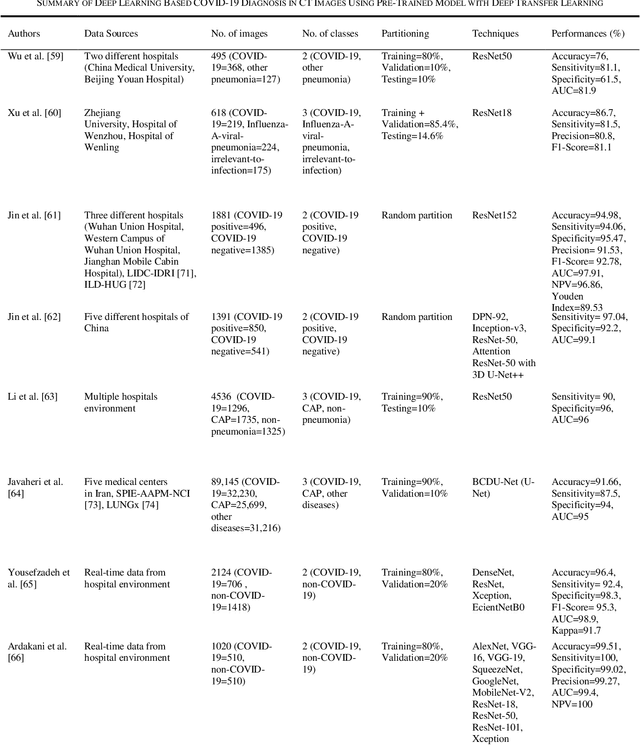
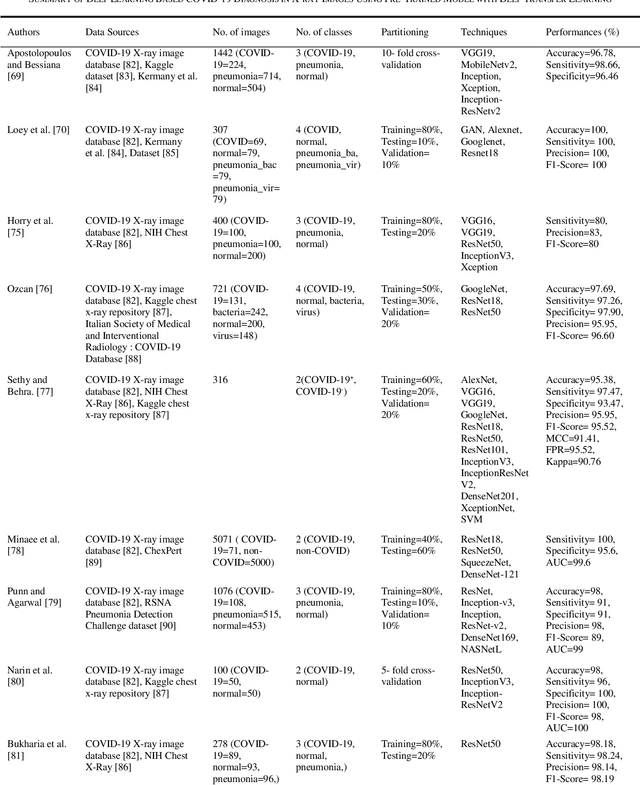
Novel coronavirus (COVID-19) outbreak, has raised a calamitous situation all over the world and has become one of the most acute and severe ailments in the past hundred years. The prevalence rate of COVID-19 is rapidly rising every day throughout the globe. Although no vaccines for this pandemic have been discovered yet, deep learning techniques proved themselves to be a powerful tool in the arsenal used by clinicians for the automatic diagnosis of COVID-19. This paper aims to overview the recently developed systems based on deep learning techniques using different medical imaging modalities like Computer Tomography (CT) and X-ray. This review specifically discusses the systems developed for COVID-19 diagnosis using deep learning techniques and provides insights on well-known data sets used to train these networks. It also highlights the data partitioning techniques and various performance measures developed by researchers in this field. A taxonomy is drawn to categorize the recent works for proper insight. Finally, we conclude by addressing the challenges associated with the use of deep learning methods for COVID-19 detection and probable future trends in this research area. This paper is intended to provide experts (medical or otherwise) and technicians with new insights into the ways deep learning techniques are used in this regard and how they potentially further works in combatting the outbreak of COVID-19.

Batch-Incremental Triplet Sampling for Training Triplet Networks Using Bayesian Updating Theorem

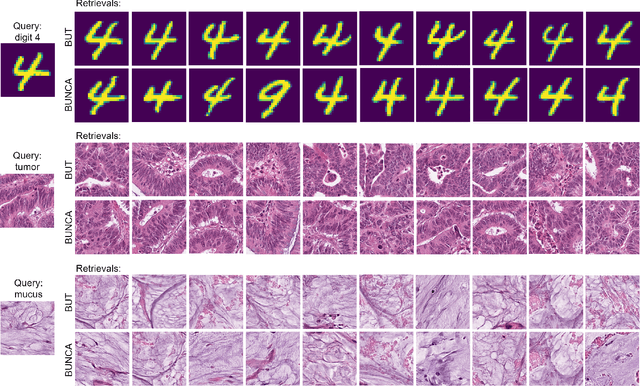
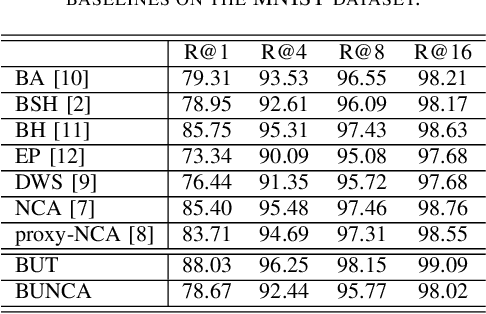
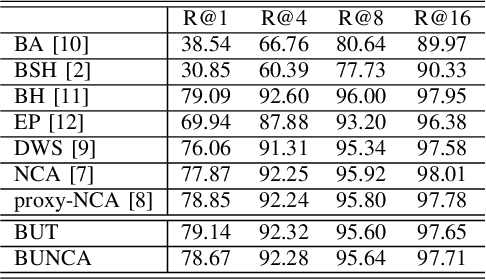
Variants of Triplet networks are robust entities for learning a discriminative embedding subspace. There exist different triplet mining approaches for selecting the most suitable training triplets. Some of these mining methods rely on the extreme distances between instances, and some others make use of sampling. However, sampling from stochastic distributions of data rather than sampling merely from the existing embedding instances can provide more discriminative information. In this work, we sample triplets from distributions of data rather than from existing instances. We consider a multivariate normal distribution for the embedding of each class. Using Bayesian updating and conjugate priors, we update the distributions of classes dynamically by receiving the new mini-batches of training data. The proposed triplet mining with Bayesian updating can be used with any triplet-based loss function, e.g., triplet-loss or Neighborhood Component Analysis (NCA) loss. Accordingly, Our triplet mining approaches are called Bayesian Updating Triplet (BUT) and Bayesian Updating NCA (BUNCA), depending on which loss function is being used. Experimental results on two public datasets, namely MNIST and histopathology colorectal cancer (CRC), substantiate the effectiveness of the proposed triplet mining method.

Offline versus Online Triplet Mining based on Extreme Distances of Histopathology Patches

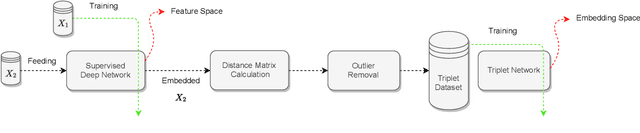
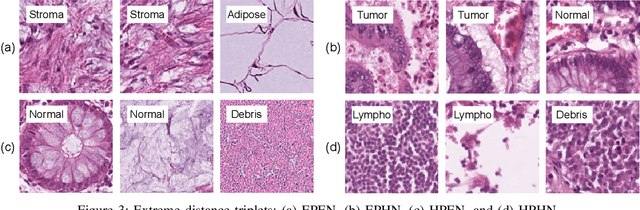
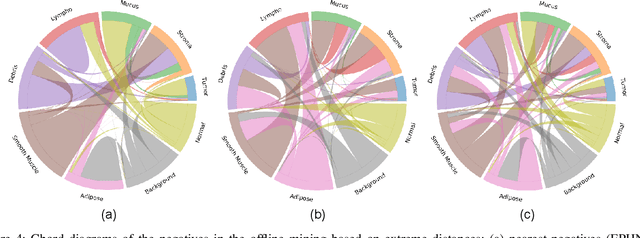
We analyze the effect of offline and online triplet mining for colorectal cancer (CRC) histopathology dataset containing 100,000 patches. We consider the extreme, i.e., farthest and nearest patches with respect to a given anchor, both in online and offline mining. While many works focus solely on how to select the triplets online (batch-wise), we also study the effect of extreme distances and neighbor patches before training in an offline fashion. We analyze the impacts of extreme cases for offline versus online mining, including easy positive, batch semi-hard, and batch hard triplet mining as well as the neighborhood component analysis loss, its proxy version, and distance weighted sampling. We also investigate online approaches based on extreme distance and comprehensively compare the performance of offline and online mining based on the data patterns and explain offline mining as a tractable generalization of the online mining with large mini-batch size. As well, we discuss the relations of different colorectal tissue types in terms of extreme distances. We found that offline mining can generate a better statistical representation of the population by working on the whole dataset.

Roweisposes, Including Eigenposes, Supervised Eigenposes, and Fisherposes, for 3D Action Recognition

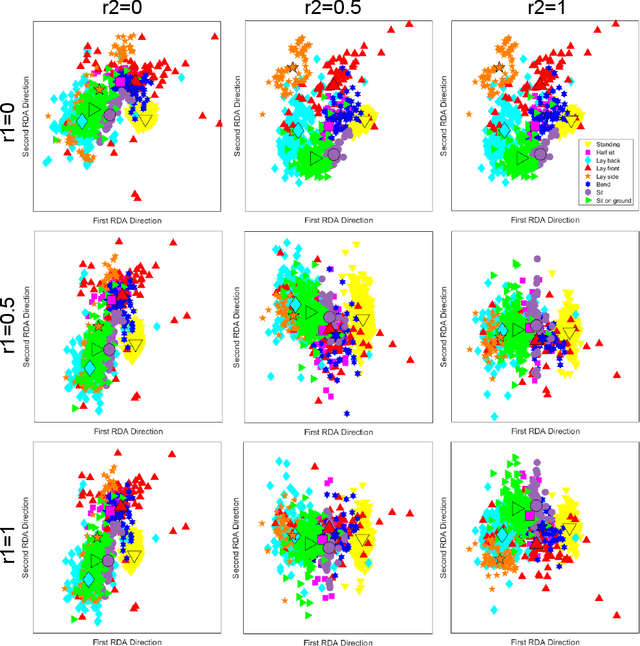
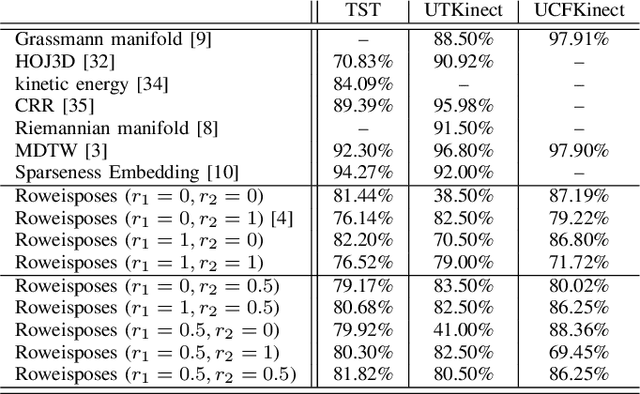
Human action recognition is one of the important fields of computer vision and machine learning. Although various methods have been proposed for 3D action recognition, some of which are basic and some use deep learning, the need of basic methods based on generalized eigenvalue problem is sensed for action recognition. This need is especially sensed because of having similar basic methods in the field of face recognition such as eigenfaces and Fisherfaces. In this paper, we propose Roweisposes which uses Roweis discriminant analysis for generalized subspace learning. This method includes Fisherposes, eigenposes, supervised eigenposes, and double supervised eigenposes as its special cases. Roweisposes is a family of infinite number of action recongition methods which learn a discriminative subspace for embedding the body poses. Experiments on the TST, UTKinect, and UCFKinect datasets verify the effectiveness of the proposed method for action recognition.

Quantile-Quantile Embedding for Distribution Transformation, Manifold Embedding, and Image Embedding with Choice of Embedding Distribution

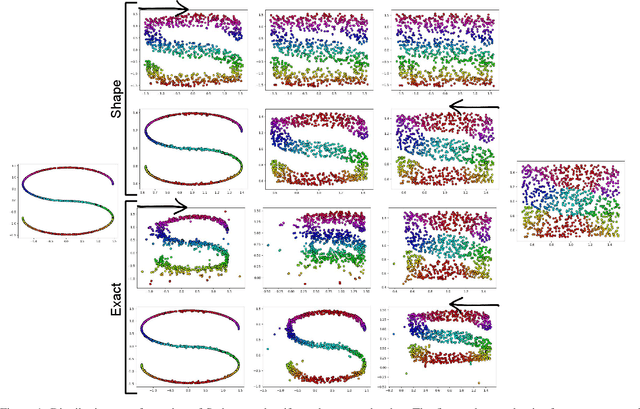
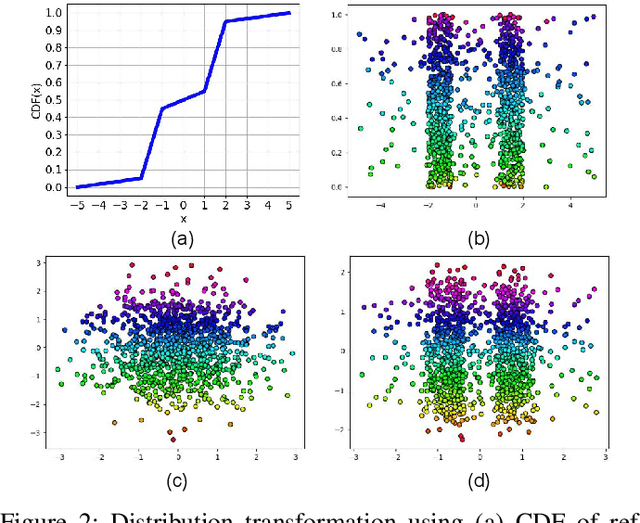
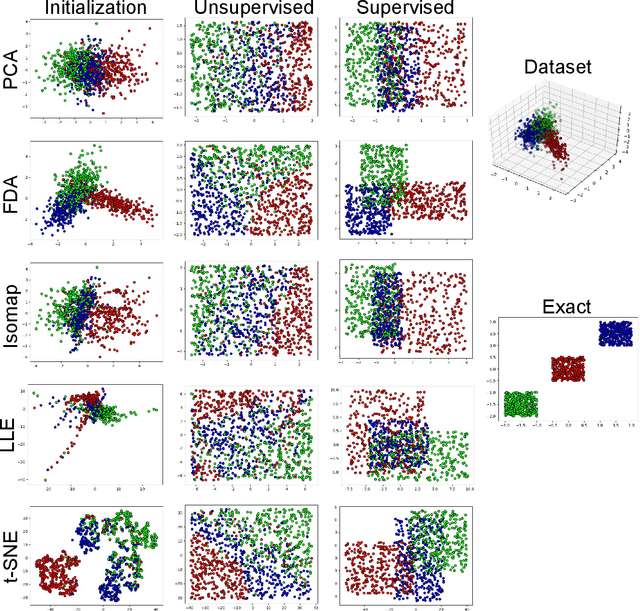
We propose a new embedding method, named Quantile-Quantile Embedding (QQE), for distribution transformation, manifold embedding, and image embedding with the ability to choose the embedding distribution. QQE, which uses the concept of quantile-quantile plot from visual statistical tests, can transform the distribution of data to any theoretical desired distribution or empirical reference sample. Moreover, QQE gives the user a choice of embedding distribution in embedding manifold of data into the low dimensional embedding space. It can also be used for modifying the embedding distribution of different dimensionality reduction methods, either basic or deep ones, for better representation or visualization of data. We propose QQE in both unsupervised and supervised manners. QQE can also transform the distribution to either the exact reference distribution or shape of the reference distribution; and one of its many applications is better discrimination of classes. Our experiments on different synthetic and image datasets show the effectiveness of the proposed embedding method.

Backprojection for Training Feedforward Neural Networks in the Input and Feature Spaces

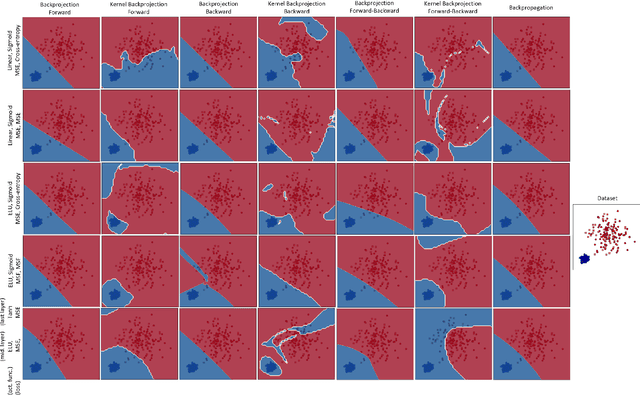
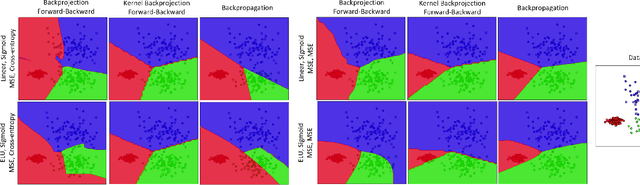
After the tremendous development of neural networks trained by backpropagation, it is a good time to develop other algorithms for training neural networks to gain more insights into networks. In this paper, we propose a new algorithm for training feedforward neural networks which is fairly faster than backpropagation. This method is based on projection and reconstruction where, at every layer, the projected data and reconstructed labels are forced to be similar and the weights are tuned accordingly layer by layer. The proposed algorithm can be used for both input and feature spaces, named as backprojection and kernel backprojection, respectively. This algorithm gives an insight to networks with a projection-based perspective. The experiments on synthetic datasets show the effectiveness of the proposed method.

Anomaly Detection and Prototype Selection Using Polyhedron Curvature

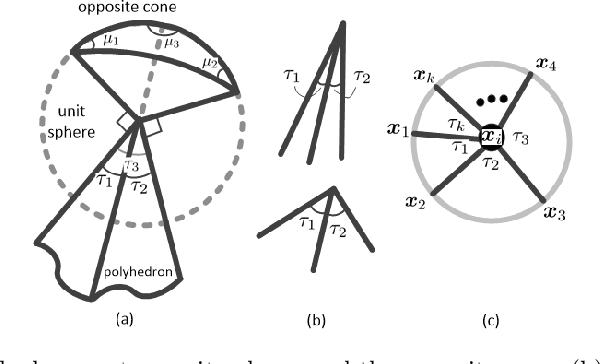
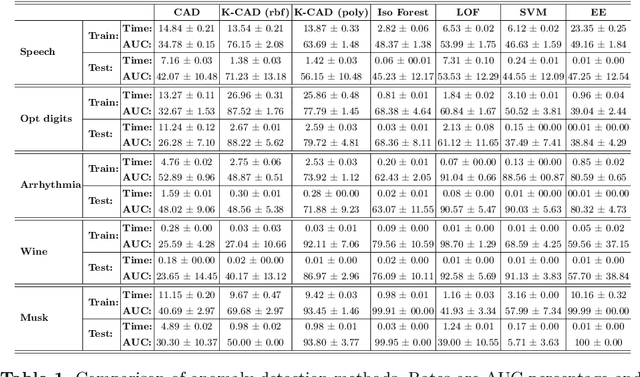
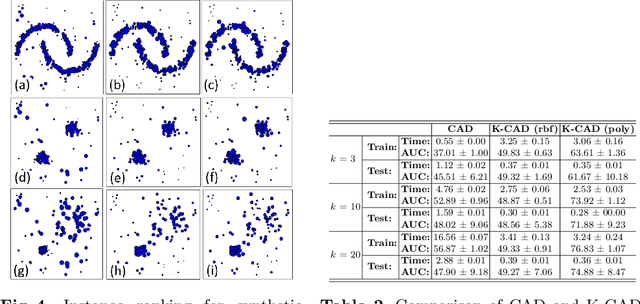
We propose a novel approach to anomaly detection called Curvature Anomaly Detection (CAD) and Kernel CAD based on the idea of polyhedron curvature. Using the nearest neighbors for a point, we consider every data point as the vertex of a polyhedron where the more anomalous point has more curvature. We also propose inverse CAD (iCAD) and Kernel iCAD for instance ranking and prototype selection by looking at CAD from an opposite perspective. We define the concept of anomaly landscape and anomaly path and we demonstrate an application for it which is image denoising. The proposed methods are straightforward and easy to implement. Our experiments on different benchmarks show that the proposed methods are effective for anomaly detection and prototype selection.