Hierarchical Subspace Learning for Dimensionality Reduction to Improve Classification Accuracy in Large Data Sets

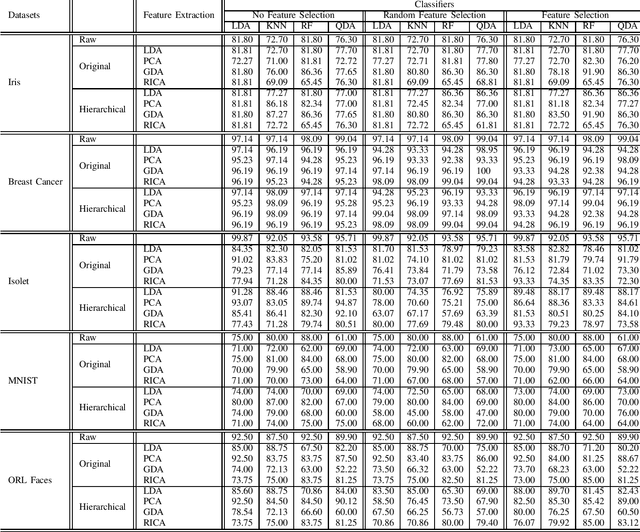
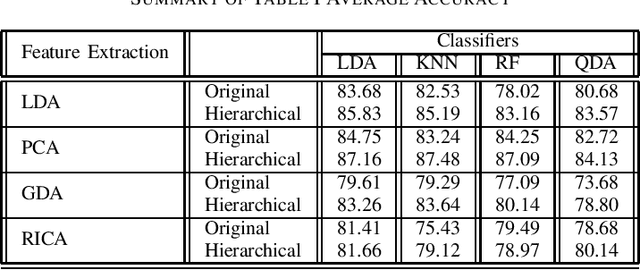
Manifold learning is used for dimensionality reduction, with the goal of finding a projection subspace to increase and decrease the inter- and intraclass variances, respectively. However, a bottleneck for subspace learning methods often arises from the high dimensionality of datasets. In this paper, a hierarchical approach is proposed to scale subspace learning methods, with the goal of improving classification in large datasets by a range of 3% to 10%. Different combinations of methods are studied. We assess the proposed method on five publicly available large datasets, for different eigen-value based subspace learning methods such as linear discriminant analysis, principal component analysis, generalized discriminant analysis, and reconstruction independent component analysis. To further examine the effect of the proposed method on various classification methods, we fed the generated result to linear discriminant analysis, quadratic linear analysis, k-nearest neighbor, and random forest classifiers. The resulting classification accuracies are compared to show the effectiveness of the hierarchical approach, reporting results of an average of 5% increase in classification accuracy.

Acceleration of Large Margin Metric Learning for Nearest Neighbor Classification Using Triplet Mining and Stratified Sampling

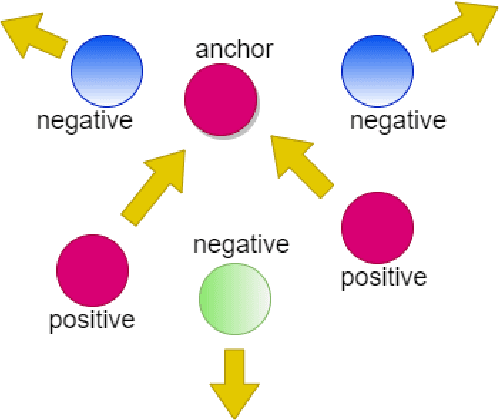
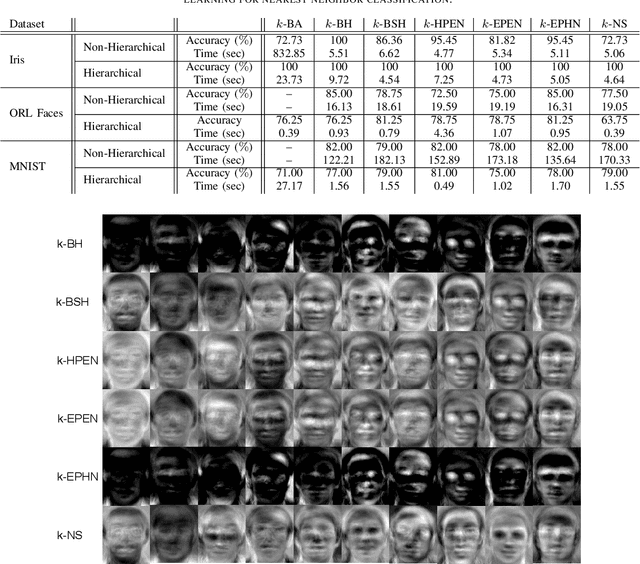
Metric learning is one of the techniques in manifold learning with the goal of finding a projection subspace for increasing and decreasing the inter- and intra-class variances, respectively. Some of the metric learning methods are based on triplet learning with anchor-positive-negative triplets. Large margin metric learning for nearest neighbor classification is one of the fundamental methods to do this. Recently, Siamese networks have been introduced with the triplet loss. Many triplet mining methods have been developed for Siamese networks; however, these techniques have not been applied on the triplets of large margin metric learning for nearest neighbor classification. In this work, inspired by the mining methods for Siamese networks, we propose several triplet mining techniques for large margin metric learning. Moreover, a hierarchical approach is proposed, for acceleration and scalability of optimization, where triplets are selected by stratified sampling in hierarchical hyper-spheres. We analyze the proposed methods on three publicly available datasets, i.e., Fisher Iris, ORL faces, and MNIST datasets.

Efficient Hardware Realization of Convolutional Neural Networks using Intra-Kernel Regular Pruning

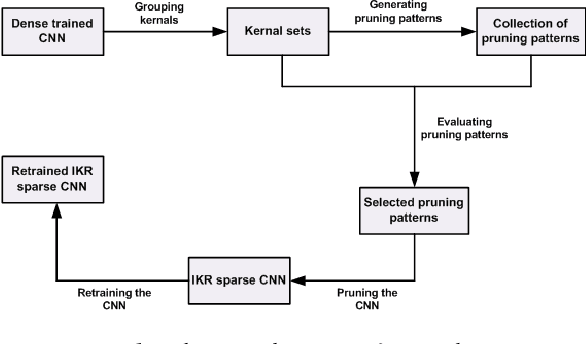
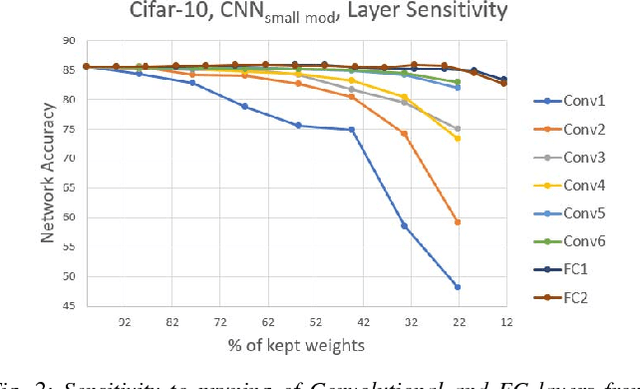
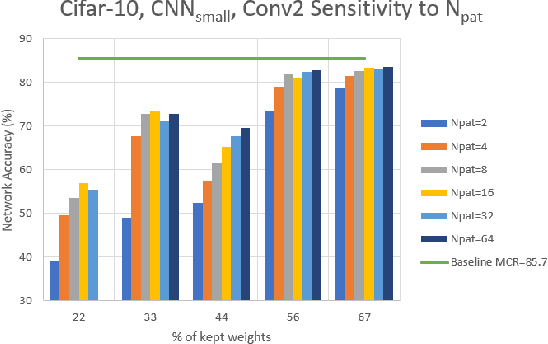
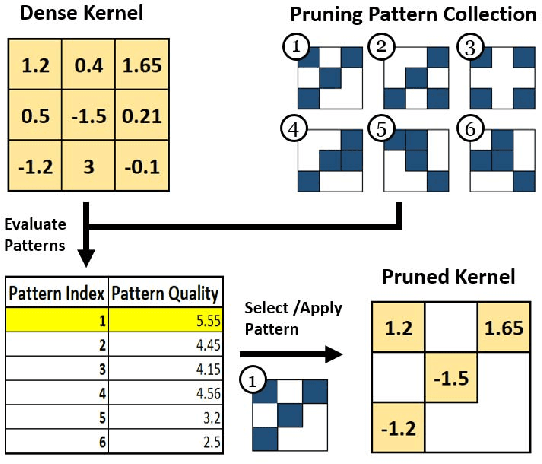
The recent trend toward increasingly deep convolutional neural networks (CNNs) leads to a higher demand of computational power and memory storage. Consequently, the deployment of CNNs in hardware has become more challenging. In this paper, we propose an Intra-Kernel Regular (IKR) pruning scheme to reduce the size and computational complexity of the CNNs by removing redundant weights at a fine-grained level. Unlike other pruning methods such as Fine-Grained pruning, IKR pruning maintains regular kernel structures that are exploitable in a hardware accelerator. Experimental results demonstrate up to 10x parameter reduction and 7x computational reduction at a cost of less than 1% degradation in accuracy versus the un-pruned case.