Graph neural networks extrapolate out-of-distribution for shortest paths

Neural networks (NNs), despite their success and wide adoption, still struggle to extrapolate out-of-distribution (OOD), i.e., to inputs that are not well-represented by their training dataset. Addressing the OOD generalization gap is crucial when models are deployed in environments significantly different from the training set, such as applying Graph Neural Networks (GNNs) trained on small graphs to large, real-world graphs. One promising approach for achieving robust OOD generalization is the framework of neural algorithmic alignment, which incorporates ideas from classical algorithms by designing neural architectures that resemble specific algorithmic paradigms (e.g. dynamic programming). The hope is that trained models of this form would have superior OOD capabilities, in much the same way that classical algorithms work for all instances. We rigorously analyze the role of algorithmic alignment in achieving OOD generalization, focusing on graph neural networks (GNNs) applied to the canonical shortest path problem. We prove that GNNs, trained to minimize a sparsity-regularized loss over a small set of shortest path instances, exactly implement the Bellman-Ford (BF) algorithm for shortest paths. In fact, if a GNN minimizes this loss within an error of $\epsilon$, it implements the BF algorithm with an error of $O(\epsilon)$. Consequently, despite limited training data, these GNNs are guaranteed to extrapolate to arbitrary shortest-path problems, including instances of any size. Our empirical results support our theory by showing that NNs trained by gradient descent are able to minimize this loss and extrapolate in practice.

Neural approximation of Wasserstein distance via a universal architecture for symmetric and factorwise group invariant functions

Learning distance functions between complex objects, such as the Wasserstein distance to compare point sets, is a common goal in machine learning applications. However, functions on such complex objects (e.g., point sets and graphs) are often required to be invariant to a wide variety of group actions e.g. permutation or rigid transformation. Therefore, continuous and symmetric product functions (such as distance functions) on such complex objects must also be invariant to the product of such group actions. We call these functions symmetric and factor-wise group invariant (or SFGI functions in short). In this paper, we first present a general neural network architecture for approximating SFGI functions. The main contribution of this paper combines this general neural network with a sketching idea to develop a specific and efficient neural network which can approximate the $p$-th Wasserstein distance between point sets. Very importantly, the required model complexity is independent of the sizes of input point sets. On the theoretical front, to the best of our knowledge, this is the first result showing that there exists a neural network with the capacity to approximate Wasserstein distance with bounded model complexity. Our work provides an interesting integration of sketching ideas for geometric problems with universal approximation of symmetric functions. On the empirical front, we present a range of results showing that our newly proposed neural network architecture performs comparatively or better than other models (including a SOTA Siamese Autoencoder based approach). In particular, our neural network generalizes significantly better and trains much faster than the SOTA Siamese AE. Finally, this line of investigation could be useful in exploring effective neural network design for solving a broad range of geometric optimization problems (e.g., $k$-means in a metric space).

The Weisfeiler-Lehman Distance: Reinterpretation and Connection with GNNs

In this paper, we present a novel interpretation of the so-called Weisfeiler-Lehman (WL) distance, introduced by Chen et al. (2022), using concepts from stochastic processes. The WL distance aims at comparing graphs with node features, has the same discriminative power as the classic Weisfeiler-Lehman graph isomorphism test and has deep connections to the Gromov-Wasserstein distance. This new interpretation connects the WL distance to the literature on distances for stochastic processes, which also makes the interpretation of the distance more accessible and intuitive. We further explore the connections between the WL distance and certain Message Passing Neural Networks, and discuss the implications of the WL distance for understanding the Lipschitz property and the universal approximation results for these networks.

Weisfeiler-Lehman meets Gromov-Wasserstein

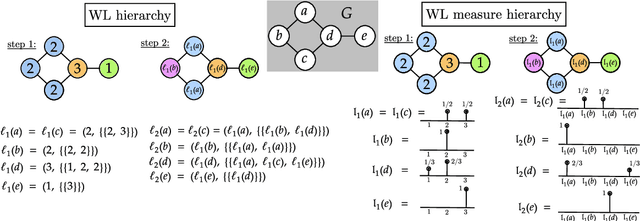
The Weisfeiler-Lehman (WL) test is a classical procedure for graph isomorphism testing. The WL test has also been widely used both for designing graph kernels and for analyzing graph neural networks. In this paper, we propose the Weisfeiler-Lehman (WL) distance, a notion of distance between labeled measure Markov chains (LMMCs), of which labeled graphs are special cases. The WL distance is polynomial time computable and is also compatible with the WL test in the sense that the former is positive if and only if the WL test can distinguish the two involved graphs. The WL distance captures and compares subtle structures of the underlying LMMCs and, as a consequence of this, it is more discriminating than the distance between graphs used for defining the state-of-the-art Wasserstein Weisfeiler-Lehman graph kernel. Inspired by the structure of the WL distance we identify a neural network architecture on LMMCs which turns out to be universal w.r.t. continuous functions defined on the space of all LMMCs (which includes all graphs) endowed with the WL distance. Finally, the WL distance turns out to be stable w.r.t. a natural variant of the Gromov-Wasserstein (GW) distance for comparing metric Markov chains that we identify. Hence, the WL distance can also be construed as a polynomial time lower bound for the GW distance which is in general NP-hard to compute.