FedOPAL: One-Shot Federated Learning via Analytic Visual Prompt Tuning

With the widespread deployment of basic models in edge intelligence, communication bandwidth has become a core bottleneck restricting the scalability of federated learning. Although one-shot federated learning alleviates this problem by minimizing communication rounds, existing iterative fine-tuning or knowledge distillation methods still face challenges such as high server-side computational costs and hyperparameter sensitivity. Analytical federated learning achieves efficient gradientfree aggregation using least-squares closed-form solutions, but in environments with non-independent and identically distributed data, its static feature assumptions fail, leading to feature manifold misalignment and severely impairing model performance. To address this contradiction, this paper proposes the FedOPAL framework. This framework adapts the visual prompts as feature rectifiers, actively correcting the feature distribution of heterogeneous data to a linearly separable space by applying local proximal constraints, thereby satisfying the theoretical assumptions of analytical federated learning. Experimental results show that FedOPAL not only significantly outperforms the original analytical methods on several benchmarks, but also achieves accuracy comparable to state-of-the-art iterative methods while maintaining zero server-side training costs, providing a new engineering paradigm for efficient collaboration of large models on the edge.

Towards One-shot Federated Learning: Advances, Challenges, and Future Directions

One-shot FL enables collaborative training in a single round, eliminating the need for iterative communication, making it particularly suitable for use in resource-constrained and privacy-sensitive applications. This survey offers a thorough examination of One-shot FL, highlighting its distinct operational framework compared to traditional federated approaches. One-shot FL supports resource-limited devices by enabling single-round model aggregation while maintaining data locality. The survey systematically categorizes existing methodologies, emphasizing advancements in client model initialization, aggregation techniques, and strategies for managing heterogeneous data distributions. Furthermore, we analyze the limitations of current approaches, particularly in terms of scalability and generalization in non-IID settings. By analyzing cutting-edge techniques and outlining open challenges, this survey aspires to provide a comprehensive reference for researchers and practitioners aiming to design and implement One-shot FL systems, advancing the development and adoption of One-shot FL solutions in a real-world, resource-constrained scenario.

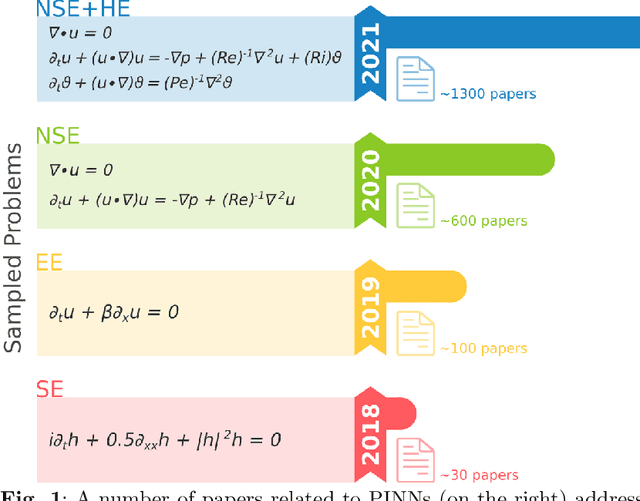
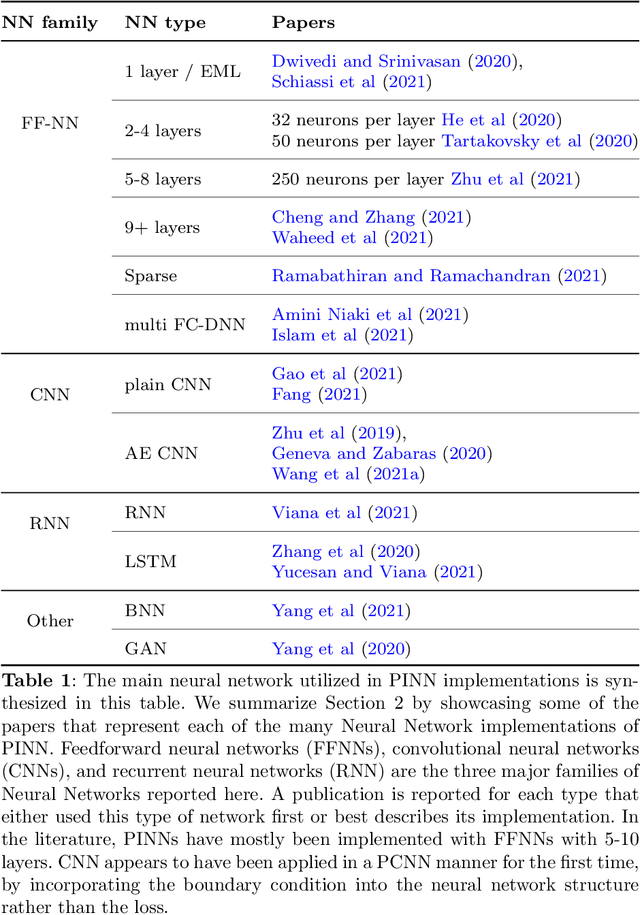
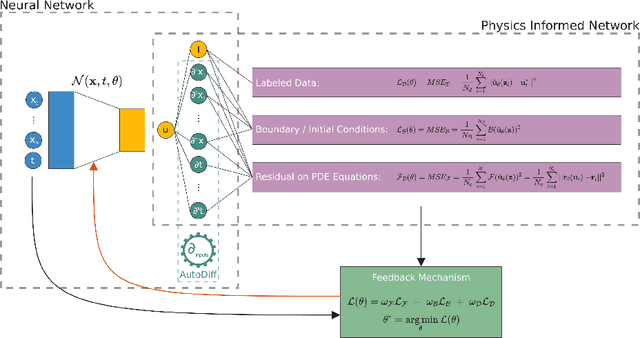
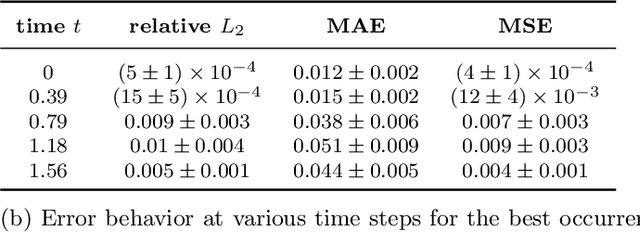
Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What's next

Physics-Informed Neural Networks (PINN) are neural networks (NNs) that encode model equations, like Partial Differential Equations (PDE), as a component of the neural network itself. PINNs are nowadays used to solve PDEs, fractional equations, and integral-differential equations. This novel methodology has arisen as a multi-task learning framework in which a NN must fit observed data while reducing a PDE residual. This article provides a comprehensive review of the literature on PINNs: while the primary goal of the study was to characterize these networks and their related advantages and disadvantages, the review also attempts to incorporate publications on a larger variety of issues, including physics-constrained neural networks (PCNN), where the initial or boundary conditions are directly embedded in the NN structure rather than in the loss functions. The study indicates that most research has focused on customizing the PINN through different activation functions, gradient optimization techniques, neural network structures, and loss function structures. Despite the wide range of applications for which PINNs have been used, by demonstrating their ability to be more feasible in some contexts than classical numerical techniques like Finite Element Method (FEM), advancements are still possible, most notably theoretical issues that remain unresolved.